フリーでオープンソースの有限要素法ライブラリです。多種多様な解析機能の他に、簡単なモデル生成機能やメッシュ生成機能、可視化機能がついており、誰でも簡単に数値解析を行うことを目指しています。
| 有限要素法(FEM)は偏微分方程式を解いたり力学解析をする上で非常に強力な方法です。 何十年にもわたり様々な研究が精力的になされ、この手法は目まぐるしく発展してきました。 しかし大企業の開発者や大学の研究者など、ごく一部の限られた人以外はその恩恵を被ることができないのが現状です。 誰でも簡単に有限要素法を理解して使えるようになることに少しでも役に立つことを、 このWebページを通じて目指しています。 |
|
フリーでオープンソースの有限要素法ライブラリです。多種多様な解析機能の他に、簡単なモデル生成機能やメッシュ生成機能、可視化機能がついており、誰でも簡単に数値解析を行うことを目指しています。 | ||
|
○ uMesh (ver 1.0.4 β)
[27.sep.2007] このソフトウェアは有限要素法のための２次元３角形メッシュを作成するものです。 簡単なモデラーも内蔵しており２次元形状を作成することができます。
|
 |
||||
|
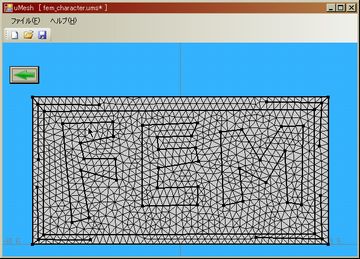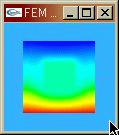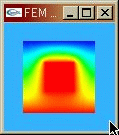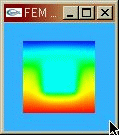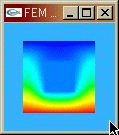
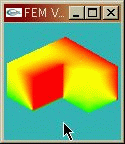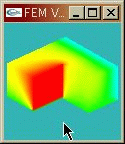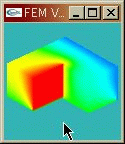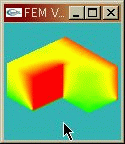
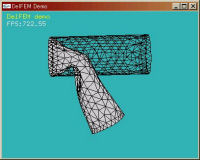
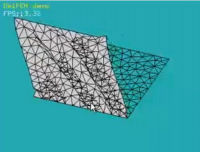
○ FEM demo : Laplace's Equation このプログラムは２次元Laplace方程式を解いて３次元上に表示するプログラムです。 マウスドラッグによって固定境界条件を指定することができ、 リアルタイムで解が更新されます。 |
 |
||
|
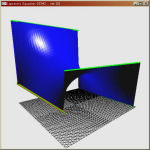○ Function Viewer 2D 数式を入力すると３次元上に表示してくれるソフトです。時間依存の数式に対応しています。 Enter a mathematical function, and this program will render the function in a 3D space. You can change viewpoint arbitrary with an intuitive operation. This progtram can deal with time dependent functions. |
 |
|
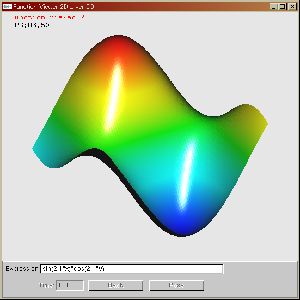大分昔に勉強した数値計算（特に有限要素法と連立一次方程式ソルバ）関連のことを忘れないためにまとめています。最初にお断りしておきますが、このドキュメントはかなり独断と偏見に満ち溢れたのになってます。専門家の目からみると「そりゃ、間違えや」と言われてしまうような内容も多少あると思います。したがって、これを数値計算のきちんとした解説だと考えないで下さい。しかし、とにかく雰囲気を手っ取り早くつかんで理解するようになるには(ある程度)役立つんじゃないかと思います。指摘、意見、感想などは大歓迎です。 It is only a memorandum no to foget. |
|
| |
| ○ 有限要素法の概要(工事中) [2009/11/11] | |
| ○ ポアソン方程式の有限要素法による数値解法 [2007/07/03] | |
○ 熱拡散方程式の有限要素法による数値解法 [2009/05/17]
| |
| ○ 移流拡散方程式の有限要素法による数値解法 [2007/01/03] | |
○ 陰的時間積分スキーム 
| |
○ 線形弾性体の有限要素法による数値解法
 ３次元動的線形弾性体
| |
|
○ Total-Lagrange法による幾何学的非線形弾性体の有限要素法解析
幾何学的非線形を考慮した引っ張り
| |
|
○ サンブナン体の有限要素法による数値解法
幾何学的非線形を考慮した引っ張り
２次元弾性体への境界条件のインタラクティブな設定
| |
|
○ 超弾性体の有限要素法解析
非圧縮性超弾性体のリアルタイム有限要素法解析
| |
|
○ DKT要素による薄板の有限要素法解析
線形DKTシェル要素による，非定常の薄肉円筒の振動解析
| |
|
○ MITC要素によるシェルの有限要素法解析
| |
|
○ ２次元薄肉梁要素の有限要素法解析 [2009/10/25]
| |
| ○ 圧力剛性行列 [2009/03/07] | |
|
○ ラグランジュ未定乗数による多点拘束(MPC)
ラグランジュ未定乗数法を用いた変位の直線上への拘束
剛体への節点の貼り付け３
非線形弾性体と機構解析の連成解析
| |
|
○ Kuhn-Tucker条件による簡単な接触解析
Kuhn-Tucker条件を用いた剛体平面と線形弾性体の準静的な接触解析
剛体円と線形弾性梁の２次元接触問題
剛体円とSt.Venant-Kirchhoff体の接触の動解析
| |
|
○ 有限要素法による簡単な音場解析
Helmholtz方程式の可視化
| |
|
○ 有限要素法のためのデータ構造
|
|
| |
| ○ 流体のための連続体力学 [2006/12/23] | |
| ○ 流体の支配方程式 [2006/12/23] | |
|
○ 応力速度
| |
|
○ 剛体の運動
|
|
| |
| ○ ヒルベルト空間 [17.Jun.2008] | |
| ○ 線形作用素 [17.Jun.2008] | |
|
○ 有限要素法の数学的基礎 [09.Oct.2007] | |
|
○ 均質化法の基礎 [10.Feb.2008] | |
|
○ ベッセル関数
|
|
| |
|
○ 共役勾配法(Conjugate Gradient法、CG法)
| |
|
○ 共役勾配法(CG法)の収束性
| |
|
○ 前処理つき共役勾配法
| |
|
○ 一般化最少残差法(GMRes法)
| |
|
○ 安定化双共役勾配法(BiCGSTAB法)
| |
| ○ 双ランチョス法(Two-Sided Lanczos 法) [08.Apr.2007] | |
| ○ Arnoldi法 [15.Jan.2007] | |
| ○ QR法 [17.Jun.2007] | |
| ○ 代数的マルチグリッド法 [15.Sep.2007] | |
|
○ LU分解
|
|
| |
|
○ メッシュ生成のプログラミングTIPS [17.Feb.2007] |
○ Simple_Poisson2D
|
||||||||||
 |
 |
||
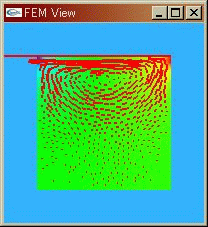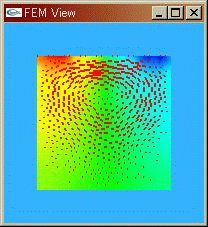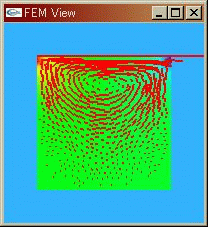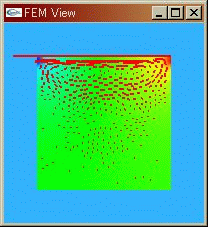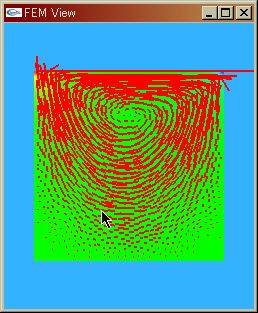| Non-Stationary Stokes | Stationary Stokes |
| 層流(Laminer Flow) |  |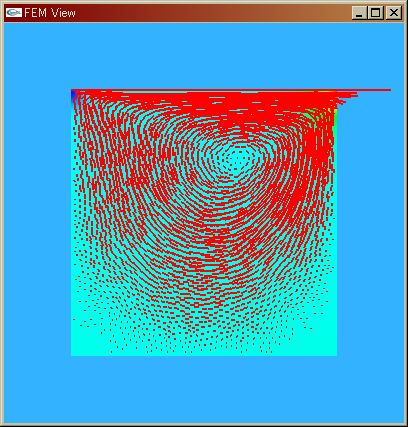
 |
 |
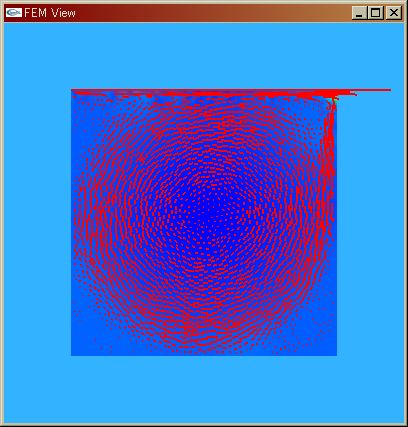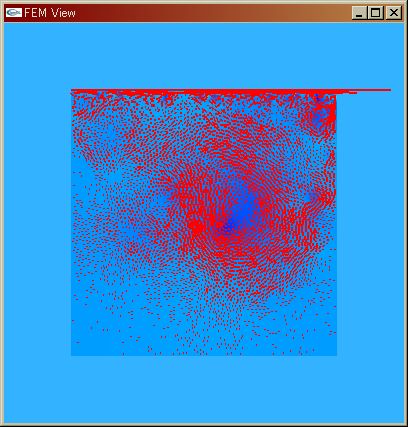
| Navier-Stokes Re=100 | Navier-Stokes Re=1^3 | Navier-Stokes Re=1^4 | |
| 乱流(Turburant) | |||||
 |
 |
 |
 |
 |
|
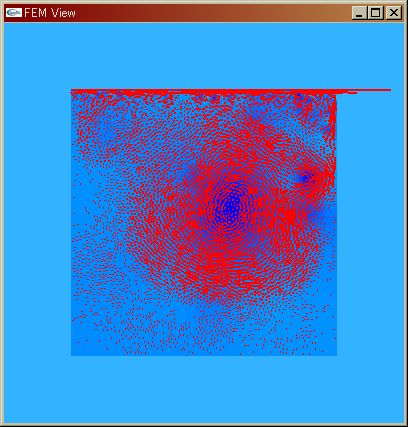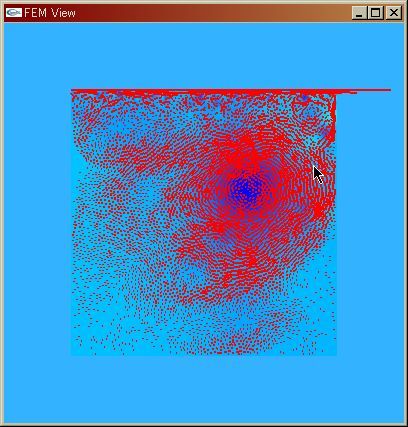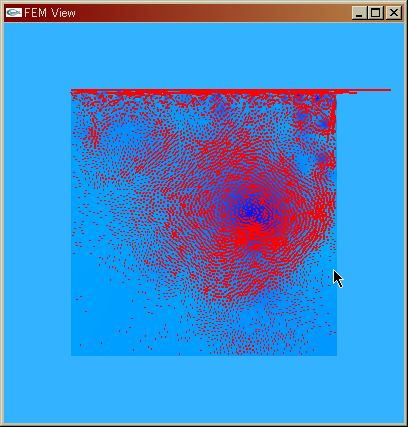
| Navier-Stokes Re=10^5 | |||||
  |
  |
|
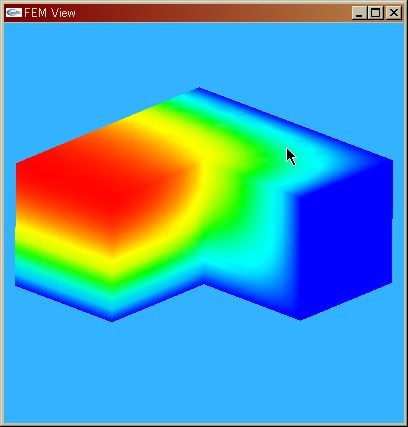
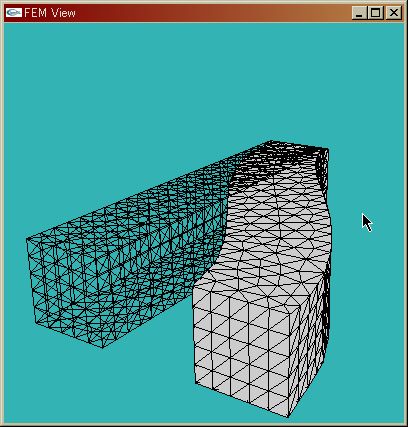
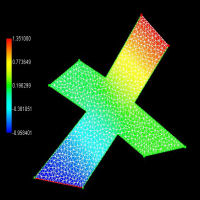
| St.Venant-Kirchhoff Material | Linear Elastic Material |
 |
 |
 |
|||
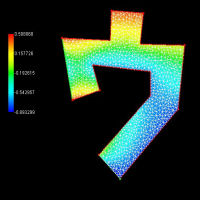
| 軸方向の圧縮による座屈 | 曲げによる座屈 | せん断変形による座屈 |
 |
 |
 |
|||
 |
 |
 |
|||
| simple modeler and mesher | graphical boundary condition setting user interface |
result viewer | |||
Sorry...... Now under development and there is no download |
|||||
 |
 |
 |
 |
|
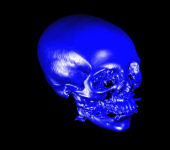
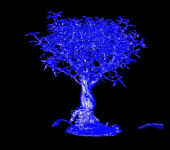
| 3D Head | Engine Block | Bonsai | TeddyBear |
 |
 |
 |
 |
 |
|
|
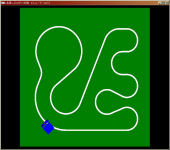
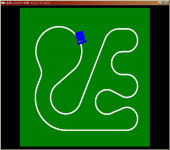
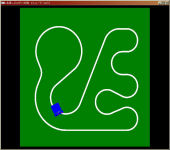
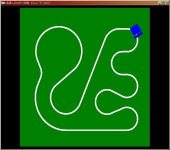
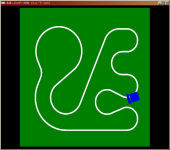
その昔、学部実験でC言語でPICマイコン用のプログラムを書いてライントレースロボットを動かす演習がありました。 専攻内でラップタイムを競っていたので、俄然やる気を出してコンピュータ上で全てシミュレーションするプログラムを書いて事前に最適な挙動を求めてみました。 (結果的にシミュレーションの内容は全く役に立たなかったのですが大体１００人中タイムは５番目でした)。 これがそのとき組んだプログラムです。 C言語ソース(要GLUT) robo.c プログラムの工夫した部分はライントレースロボのセンサーが白線の上にあるかどうかの交錯判定をOpenGLのピック処理を用いて行っている点です。 | |||||
 |
 |
||
|
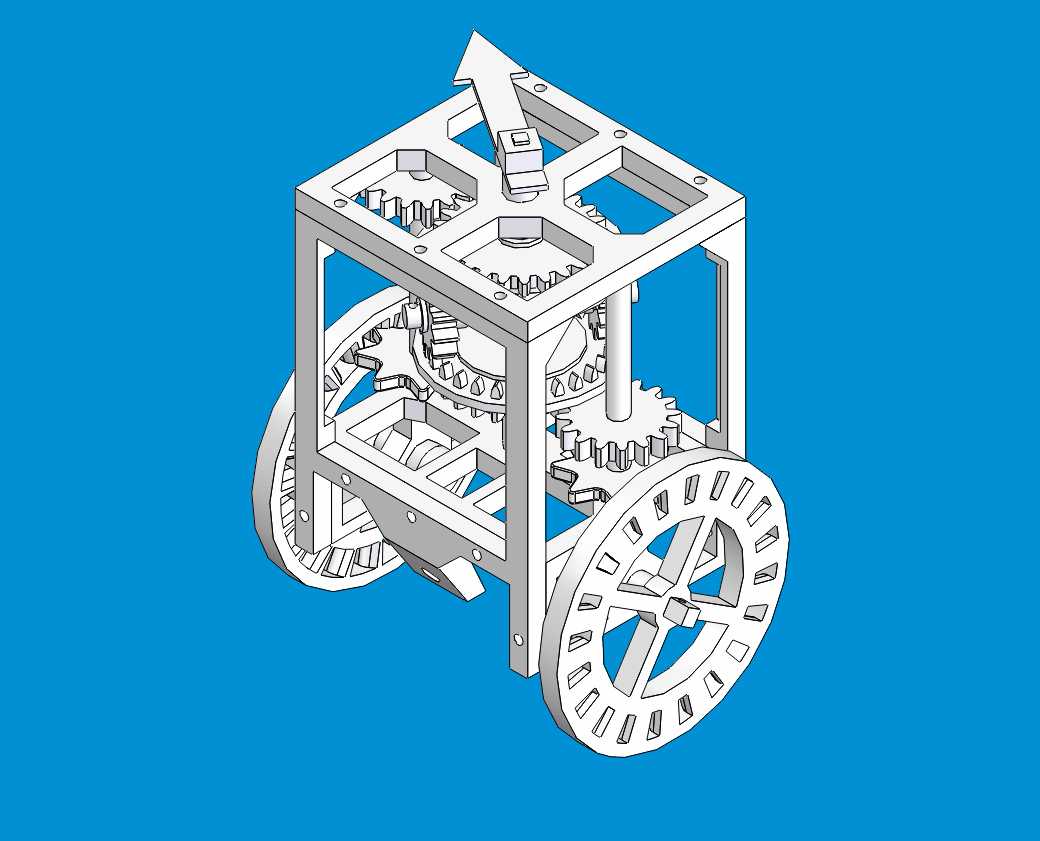
その昔、学部実験で３次元CADとRapid Prototyping Systemを使って何か面白い物を作ろうという演習がありました。 自分は５０時間以上におも及ぶ途方もない時間をモデリングに費やして指南車を作りました 特に規定の体積に収めなきゃいけなかったのでボディーの軽量化と、ギアまわりのモデリングが大変でした。 おかげで、こちらのドイツのHPでも紹介されたりしてます。 http://www.odts.de/southptr/cad.htm ちゃちく見えますけど、頑張ればそれなりに動きましたよ。 |
|||
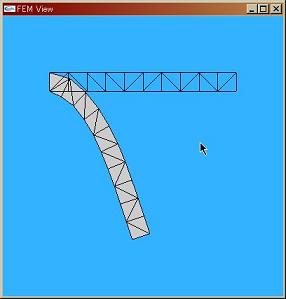
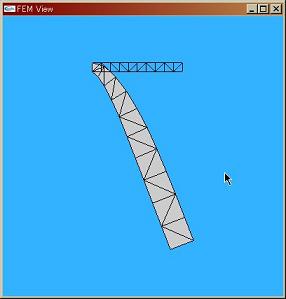
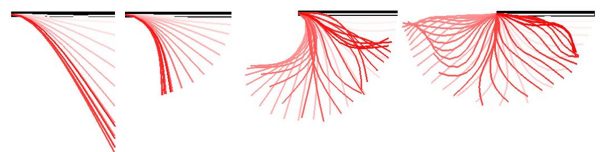
| 学部時代に３年間サークル活動で人力飛行機を設計製作していました。少人数かつ低予算のチームでもコンテストに勝てる方法を模索する中で有限要素法に出会い、独学で勉強を始めました。今ではサークルを引退していますが、自分と同じような境遇の人のために設計支援ソフトウェアを作ることを目指しています。いつまでもエンジニアリング魂を忘れたくないですね。 |
|
|
||
|
|
|
|
ダウンロード
READMEはこちら
[
