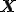 における応力は
における応力は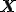 の近傍の領域の物質店の集合の過去から現在時刻
の近傍の領域の物質店の集合の過去から現在時刻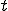 に至るまでの運動の履歴によって決定される.特に,ある物質が変形勾配
に至るまでの運動の履歴によって決定される.特に,ある物質が変形勾配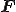 の履歴のみに依存して応力
の履歴のみに依存して応力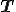 の定まる単純体(simple material)とすると次の式が成り立つ.
の定まる単純体(simple material)とすると次の式が成り立つ.|TOP Page|
構成式に関する原理Ⅰ(局所作用の原理)より,点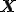 における応力は
における応力は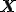 の近傍の領域の物質店の集合の過去から現在時刻
の近傍の領域の物質店の集合の過去から現在時刻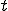 に至るまでの運動の履歴によって決定される.特に,ある物質が変形勾配
に至るまでの運動の履歴によって決定される.特に,ある物質が変形勾配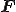 の履歴のみに依存して応力
の履歴のみに依存して応力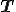 の定まる単純体(simple material)とすると次の式が成り立つ.
の定まる単純体(simple material)とすると次の式が成り立つ.
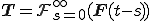
単純物質の構成式においてもし,
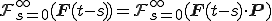
とするようななんらかの2階のテンソル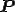 が存在する場合,この物質は変換
が存在する場合,この物質は変換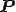 に対して対称であると呼ぶ.
に対して対称であると呼ぶ.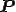 は変形
は変形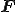 に先立つ物体の変換を表すので,対称変換(symmetric transformation)と呼ばれる.液晶などのように流体に異方性があるような特別な場合を除いて,一般的に流体は密度が変化しなければ力学特性も同一のはずであるから,
に先立つ物体の変換を表すので,対称変換(symmetric transformation)と呼ばれる.液晶などのように流体に異方性があるような特別な場合を除いて,一般的に流体は密度が変化しなければ力学特性も同一のはずであるから,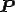 が
が
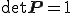
を満たす任意の変換であるとき,その物質を(単純)流体と定義することができる.なお上式を満たす変換をユニモジュラー変換(unimodular transformation)と呼ぶ.任意の回転は上式を満たすから流体は等方であることが分かる.上式の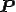 に
に

を代入すると流体の構成式は
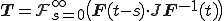
が成り立たつことが必要である.同時に上式が成り立っている場合,任意の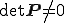 となる変換
となる変換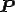 に対して
に対して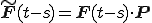 を上式に代入すると
を上式に代入すると
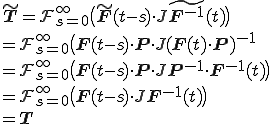
となり,変換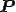 に依存しない形で表せるので,流体の構成式として十分満足する.以上から(単純)流体の構成式は次のように書けることが必要十分条件となる.
に依存しない形で表せるので,流体の構成式として十分満足する.以上から(単純)流体の構成式は次のように書けることが必要十分条件となる.
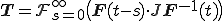
次に上式右辺の( )内が
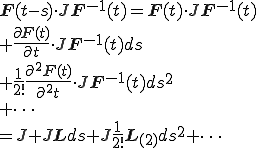
のようにTaylor展開できるものとする.但し,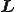 は速度勾配テンソルであり,
は速度勾配テンソルであり,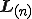 はn階の速度勾配テンソルである.もし上式右辺2項までとって残余項が十分小さくなるなら,構成式は次のように書くことができる.
はn階の速度勾配テンソルである.もし上式右辺2項までとって残余項が十分小さくなるなら,構成式は次のように書くことができる.
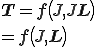
また基準配置からの体積変化率,つまりヤコビアンと密度は上式によって対応付けられるので上式からヤコビアンを除き,代わりに現在の時刻での密度の関数とすることができる.つまり,
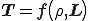
となる
ここで,流体の速度が一様,つまり速度勾配が0である場合の応力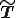 を考える.速度勾配が0である場合は
を考える.速度勾配が0である場合は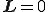 であるから,上式より
であるから,上式より
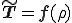
となる.また,物質客観性の原理から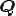 を任意の対称テンソルとすると,
を任意の対称テンソルとすると,
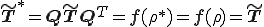
任意の対称テンソル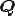 による回転に対して不変なテンソルは単位テンソル
による回転に対して不変なテンソルは単位テンソル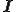 の定数倍に限られる.よってこの場合の応力
の定数倍に限られる.よってこの場合の応力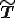 は
は
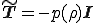
とかける.このように流体の速度が一様であるときの応力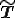 を静水圧応力(hydrostatic stress),
を静水圧応力(hydrostatic stress),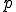 を静水圧(hydrostatic pressure)と呼ぶ.また上式のように圧力が密度だけから決定されるような流体をバロトロピー流体(Barotoropic fluid)または順圧流体と呼ぶ.また,圧力が密度以外に温度などに依存する流体を斜圧流体(baroclinic fluid)と呼ぶ.また,非圧縮性流体のように圧力が非圧縮性を満たすための拘束力として働く場合,この圧力を不定静水圧という.
を静水圧(hydrostatic pressure)と呼ぶ.また上式のように圧力が密度だけから決定されるような流体をバロトロピー流体(Barotoropic fluid)または順圧流体と呼ぶ.また,圧力が密度以外に温度などに依存する流体を斜圧流体(baroclinic fluid)と呼ぶ.また,非圧縮性流体のように圧力が非圧縮性を満たすための拘束力として働く場合,この圧力を不定静水圧という.
応力を決定する関数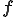 からこの静水圧応力
からこの静水圧応力 を除いた関数を新たに
を除いた関数を新たに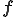 と定義すると,
と定義すると,
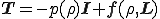
となる.但し,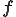 は流体の速度が一様,つまり速度勾配が0であるときの応力を応力
は流体の速度が一様,つまり速度勾配が0であるときの応力を応力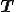 から除いたものなので,速度勾配が0である場合に
から除いたものなので,速度勾配が0である場合に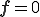 を満たさなければならない.つまり,
を満たさなければならない.つまり,
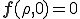
である.また常に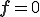 が成り立つ場合,つまり
が成り立つ場合,つまり
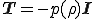
である場合,この構成式は理想流体を表す.流体の基本的物理特性は並行にあるとき剪断応力を保持できないということであるが,このような構成式で表される流体はそれが運動中にこの性質を保てるという意味で理想的なのである.理想流体において剪断応力が存在しないということは,単純剪断運動において隣り合う層が抵抗なくお互いに滑りあうことができることを意味している.粘性流体においてはこの種の相対運動は摩擦抵抗をうけ,剪断力を発生させるので理想流体は非粘性流体(inviscid fluid)といっても差し支えない.
非理想流体の場合は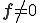 であり,
であり,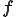 は理想流体からのずれの応力を表すので
は理想流体からのずれの応力を表すので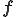 は過剰応力と呼ばれる.一般的に過剰応力は粘性による応力を表している.
は過剰応力と呼ばれる.一般的に過剰応力は粘性による応力を表している.
速度勾配テンソル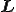 の対称成分を
の対称成分を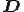 ,反対称成分を
,反対称成分を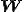 とすると,
とすると,
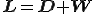
となる.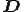 は変形速度テンソル(deformation rate tensor)
は変形速度テンソル(deformation rate tensor)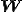 はスピンテンソル(spin tensor)と呼ばれる.
はスピンテンソル(spin tensor)と呼ばれる.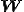 は剛体回転を表しており,応力に関係しないつまり,構成式は変形速度テンソル
は剛体回転を表しており,応力に関係しないつまり,構成式は変形速度テンソル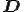 のみで表すことができると考えられる.実際のところ,物質客観性の原理より,関数
のみで表すことができると考えられる.実際のところ,物質客観性の原理より,関数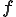 は任意の直行テンソル
は任意の直行テンソル とその時間微分で任意の反対称テンソルとなる
とその時間微分で任意の反対称テンソルとなる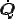 に対して
に対して
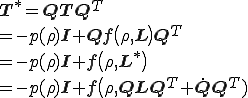
を満たさなければならない.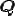 ,
,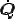 は任意であったことから,ここで
は任意であったことから,ここで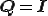 ,
,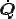 を
を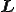 の反対称成分にマイナスしたもの
の反対称成分にマイナスしたもの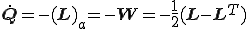 とすると
とすると
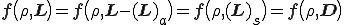
であるから,
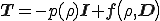
となり,過剰応力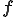 は歪速度テンソル
は歪速度テンソル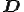 の関数となる
の関数となる
速度勾配テンソル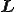 の反対称成分
の反対称成分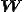 が出てきたが,一般に反対称テンソル
が出てきたが,一般に反対称テンソル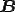 は軸性ベクトル(axial vector)
は軸性ベクトル(axial vector)
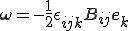
を持ち任意のベクトル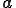 に対して
に対して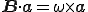 となる.スピンテンソル
となる.スピンテンソル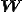 に対して軸性ベクトル
に対して軸性ベクトル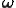 は
は
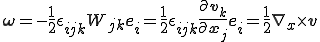
で表され,流体が剛体回転する角速度ベクトルを表している.上式より角速度ベクトル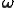 は
は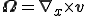 で定義される渦度ベクトル(vorticity)の半分になる.
で定義される渦度ベクトル(vorticity)の半分になる.
流体に非圧縮性の条件を仮定すれば,物質点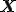 の質量密度は時間に依存せず,一定であるから以下の条件を満たすことになる.
の質量密度は時間に依存せず,一定であるから以下の条件を満たすことになる.
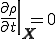
したがってこれを連続の式に適応すれば,Lagrange表示,Eular表示に対してそれぞれ非圧縮性の連続の式は以下のようになる.
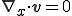
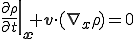
さらに単一流体,もしくは空間的に流体の密度が一定の場合
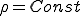
であるから,非圧縮性の条件は常に満たされ,連続の式はLagrange表示形式のみ意味を持つ.すなわち,連続の式のEular表示は常に満たされる.以上より密度一定流体の非圧縮性の式は以下のようになる.
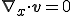
| 非圧縮性の式 |
|---|
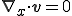 |
物質の変形に制約条件が存在する場合がある.非圧縮性の条件などに代表されるこのような制約は内部束縛(internal constraint)と呼ばれる.物体に内部束縛が存在する場合には構成式に関する原理Ⅰ(応力決定の原理)は次のように変形される必要がある.
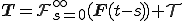
この応力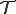 は内部仕事に無関係であり,物質点の運動,すなわち
は内部仕事に無関係であり,物質点の運動,すなわち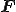 の履歴からは決定することができない応力なので非決定応力(interminate stress)と呼ばれる.非決定応力は仕事をしないので
の履歴からは決定することができない応力なので非決定応力(interminate stress)と呼ばれる.非決定応力は仕事をしないので
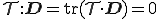
が成り立つ.
代表的な内部拘束はスカラー値テンソル関数
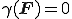
のように表される.たとえばその代表例としては非圧縮の拘束条件
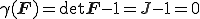
があげられる.
内部仕事も物質客観性の原理を満たさなければならないことから,
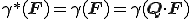
を満たさなければならない.ここで とおくと
とおくと
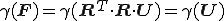
となり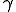 は右ストレッチテンソル
は右ストレッチテンソル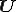 のみの関数となることが必要である.一方で右ストレッチテンソルは基準枠の回転に対して不変つまり,
のみの関数となることが必要である.一方で右ストレッチテンソルは基準枠の回転に対して不変つまり,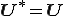 であるから
であるから
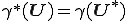
となり十分客観性を満たしていることがわかる.よって拘束条件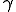 は右ストレッチテンソル
は右ストレッチテンソル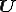 のみの関数でなければならない.
のみの関数でなければならない.
ここで非圧縮性の拘束条件にたいしてどのような非決定応力が発生するかを調べる.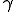 は0で定数であったので
は0で定数であったので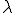 を時間微分したものも0であるはずである.よって
を時間微分したものも0であるはずである.よって
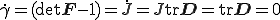
ここで拘束条件から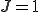 であることを用いた.上式から
であることを用いた.上式から
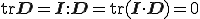
となる.よって上式から非圧縮性の制約条件が課された場合に単位テンソルの定数倍で表される応力は仕事をしないということがわかる.よって非決定応力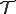 は未知数
は未知数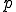 を用いて
を用いて
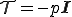
のように表すことができる.ここで導入した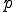 は明らかに不定静水圧である.
は明らかに不定静水圧である.
過剰応力が密度に依存しないような流体をStorks流体(Storkesian fluid)と呼び,その構成式は
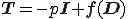
により与えられる.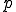 は圧力,
は圧力,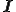 は単位テンソルである.テンソル
は単位テンソルである.テンソル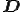 が客観性のあるテンソルであることから,物質客観性の原理により関数
が客観性のあるテンソルであることから,物質客観性の原理により関数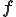 は
は
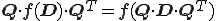
を満たさなければならない.つまり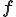 は等方テンソル関数となるから,表示定理により,
は等方テンソル関数となるから,表示定理により,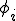 を
を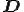 の主不変量のスカラー関数として
の主不変量のスカラー関数として

と表すことができる.上式を過剰応力とする流体はReiner-Rivlin流体とも呼ばれる.上式第3項は外力条件が急激に変化する場合に影響を持つことが知られているが,一般的に強い非線形性を示すような流体においてもほぼ無視できるほど小さいことが分かっている.
過剰応力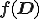 が
が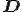 に関して線形同次であるような流体をNewton流体という.上式において
に関して線形同次であるような流体をNewton流体という.上式において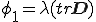 ,
,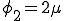 ,
,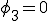 とおくと
とおくと
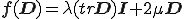
となるのでNewton流体の構成式は以下のように表すことができる.
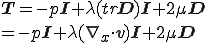
ここで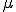 はせん断粘性率(shear viscosity),
はせん断粘性率(shear viscosity),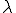 は第二粘性率(second viscosity)と呼ばれる.第二粘性率
は第二粘性率(second viscosity)と呼ばれる.第二粘性率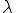 は線形弾性体におけるLameの第一定数のようなものである。
は線形弾性体におけるLameの第一定数のようなものである。
第二粘性率については以下のリンクが詳しい
| Newton流体の構成式 |
|---|
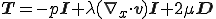 |
上式を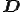 の偏差成分
の偏差成分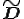
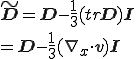
についてみると
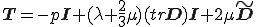
となる.ここで現れる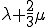 を体積粘性率(bulk viscosity)
を体積粘性率(bulk viscosity)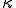 と呼ぶ.体積粘性率は流体の体積変化に伴なう粘性応力の目安である.上式は
と呼ぶ.体積粘性率は流体の体積変化に伴なう粘性応力の目安である.上式は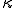 を用いて
を用いて
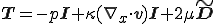
と現わすことができる.多くの流体では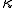 は非常に小さいことが知られている.そこで,
は非常に小さいことが知られている.そこで,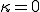 とするStokesの近似を用いると圧縮性流体の構成式は次のようになる
とするStokesの近似を用いると圧縮性流体の構成式は次のようになる

これは体積粘性係数を無視した圧縮性Newton流体の構成式である.さらに流体に非圧縮性を仮定すると
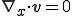
だから,非圧縮性のNewton流体の構成式は
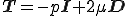
となる.
| 非圧縮性Newton流体の構成式 |
|---|
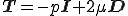 |
Newton流体の構成式は以下のとおり
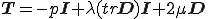
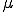 は粘性係数である.これをオイラー座標系で記述されたCauchyの第一運動法則
は粘性係数である.これをオイラー座標系で記述されたCauchyの第一運動法則
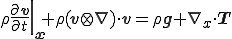
に代入して
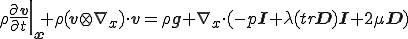
ここで
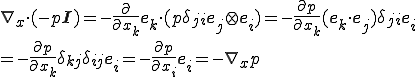
を代入すると
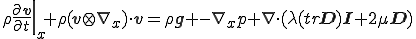
これを応力発散形式のNavier-Storks方程式と呼ぶ.
ここで粘性係数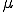 ,第二粘性係数
,第二粘性係数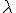 が流体中で一定とした場合について,この応力発散形式のNavier-Storks方程式を変形する.
が流体中で一定とした場合について,この応力発散形式のNavier-Storks方程式を変形する.
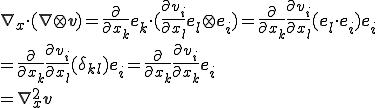
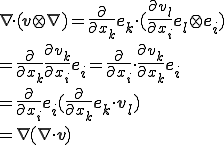
よって,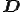 の発散は以下のように変形される.
の発散は以下のように変形される.
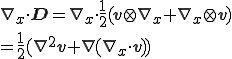
さらに,
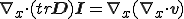
これを粘性係数,第二粘性係数が流体内で一定とした応力発散形式のNavier-Stokes方程式に代入するとNavier-Stokes方程式は
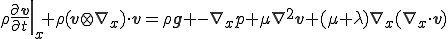
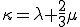 を代入して
を代入して
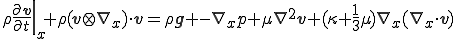
となる.ここでStokesの仮定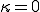 が成り立つ場合,Navier-Stokes方程式は次のようにかける.
が成り立つ場合,Navier-Stokes方程式は次のようにかける.
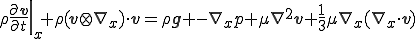
さらに流体に非圧縮性が成り立つ場合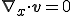 が成り立つので
が成り立つので
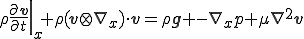
これはラプラシアン形式の非圧縮性Navier-Storks方程式と呼ばれる.
| 非圧縮性Navier-Storkes方程式 |
|---|
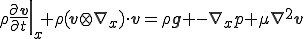 |
| 非線形有限要素法のためのテンソル解析の基礎 | 久田俊明 著 |
| 「連続体力学―簡明な理論と例題」 | P.チャドウィック 著 |