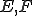 がノルム空間であるとし、
がノルム空間であるとし、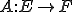 は線形写像であるとする。
は線形写像であるとする。 が有界であるというのは、ある
が有界であるというのは、ある が存在して
が存在して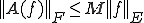 が全ての
が全ての について成り立つということである。
について成り立つということである。|TOP Page|
 がノルム空間であるとし、
がノルム空間であるとし、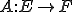 は線形写像であるとする。
は線形写像であるとする。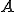 が有界であるというのは、ある
が有界であるというのは、ある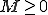 が存在して
が存在して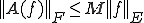 が全ての
が全ての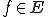 について成り立つということである。
について成り立つということである。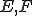 がノルム空間であるとし、
がノルム空間であるとし、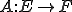 は線形写像であるとする。
は線形写像であるとする。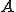 のノルム
のノルム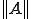 は次のように定義される
は次のように定義される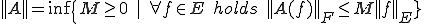
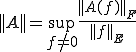
右辺について、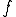 をスケーリングして
をスケーリングして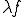 としても全く影響しないので次のような定義も可能である。
としても全く影響しないので次のような定義も可能である。
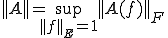
写像ノルムを見つける定石としては次のものがある
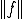 に対して、
に対して、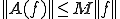 が成り立つような
が成り立つような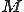 を探す。これはノルムの候補であり、ノルムと
を探す。これはノルムの候補であり、ノルムと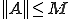 の関係にある。
の関係にある。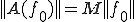 となるような
となるような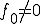 を見つけることができれば
を見つけることができれば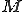 がノルム
がノルム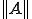 である。一般的には
である。一般的には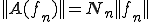 但し、
但し、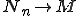 となるような列
となるような列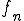 を見つけることができれば
を見つけることができれば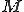 がノルム
がノルム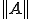 である。
である。
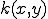 が
が![(x,y)\in [a,b]\times [a,b] (x,y)\in [a,b]\times [a,b]](4C696E656172204F70657261746F72_eq0030.gif) で定義されているとする。
で定義されているとする。
また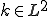 であるとする。つまり、
であるとする。つまり、
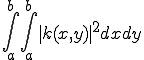
が存在し、有界である。
このとき次で定義される汎関数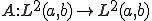 を
を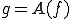 というように表す。
というように表す。
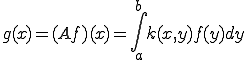
この作用素のノルムを求めてみよう。
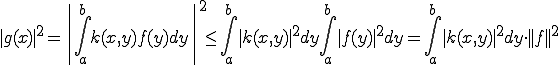
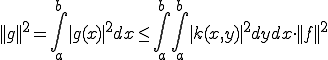
よって作用素のノルムは
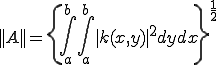
となる。
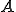 の核
の核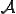 とは
とは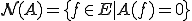
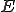 の線形部分空間である。
の線形部分空間である。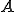 の像または値域
の像または値域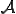 とは
とは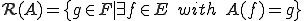
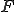 の部分空間である。
の部分空間である。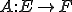 とすると、
とすると、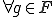 に対してある、
に対してある、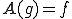 を満たすような、
を満たすような、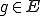 が唯一定まるとき可逆であるという。このときの
が唯一定まるとき可逆であるという。このときの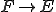 の写像を
の写像を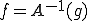 と表し、
と表し、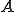 の逆と呼ぶ。
の逆と呼ぶ。
空間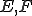 において作用素
において作用素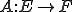 と
と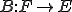 とすると
とすると
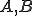 が可逆であることは、
が可逆であることは、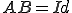 かつ
かつ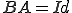 であることと同値
であることと同値
無限次元の空間ではAB=Iだけでは必ずしもAやBが可逆であることは言えないこれは注意が必要である。
例えば右シフト演算子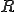 と左シフト演算子
と左シフト演算子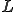 では、
では、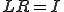 であるが、
であるが、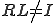 である.
である.
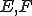 が完備距離空間、つまりバナッハ空間であるとして、有界線形作用素
が完備距離空間、つまりバナッハ空間であるとして、有界線形作用素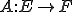 が逆を持つなら、
が逆を持つなら、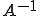 も有界な線形写像である
も有界な線形写像である
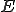 をノルムが定義された空間とし、
をノルムが定義された空間とし、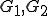 をその部分空間とする。もし
をその部分空間とする。もし
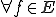 に対して
に対して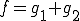 となるような、
となるような、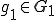 、
、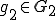 が存在する。
が存在する。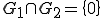
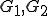 は閉空間
は閉空間
を満たすなら、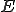 は
は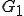 と
と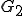 の直和といい、
の直和といい、
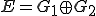
と表す
分解の一意性を示そう。
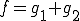 、
、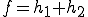 と書けたとする。但し
と書けたとする。但し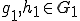 、
、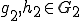
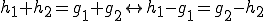
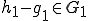 、
、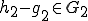 、
、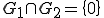
よって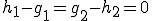
つまり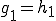 、
、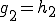 が成り立つ
が成り立つ
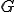 に対して、
に対して、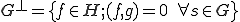 を直交補空間と呼ぶ
を直交補空間と呼ぶ
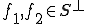 でだとして、
でだとして、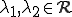 であるとすると全ての
であるとすると全ての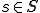 について、
について、
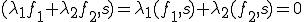
よって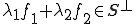 よって
よって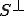 は線形空間である。
は線形空間である。
直交補空間の補空間が開集合であることを示して、直交空間が閉空間であることを示す。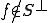 とする。つまり、
とする。つまり、
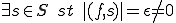
ここで、任意の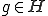 が
が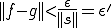 を満たすとする。
を満たすとする。
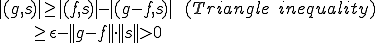
よって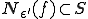 が成り立ち、
が成り立ち、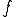 は
は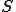 の内点
の内点
全ての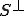 の補空間の中の点が内点なので、
の補空間の中の点が内点なので、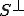 の補空間は開集合である。
の補空間は開集合である。
補空間が開集合なので、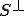 は閉集合
は閉集合
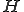 をHilbert空間であるとする。また
をHilbert空間であるとする。また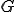 を線形閉部分空間とすると
を線形閉部分空間とすると
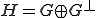
となる。
直和分解されるためには、閉空間でなければならないということに注意されたい。
直和の3つの性質が満たされるか確認してみよう。
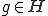 とする。
とする。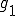 を
を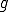 の
の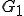 における最適近似とすると
における最適近似とすると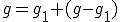 というように表したとき
というように表したとき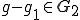 である。よって
である。よって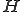 の任意の要素は
の任意の要素は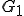 と
と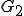 の成分の和によって表される。
の成分の和によって表される。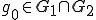 とすると、
とすると、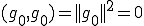 よって
よって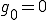
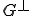 は閉集合
は閉集合以上から題意は証明された□
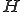 の閉部分空間を
の閉部分空間を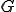 とすると、
とすると、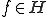 に対して
に対して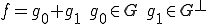
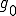 は
は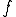 の
の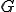 への正射影といい、
への正射影といい、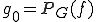 と表す。
と表す。
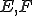 ノルム空間であるとする。
ノルム空間であるとする。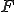 が完備、つまりバナッハ空間である場合
が完備、つまりバナッハ空間である場合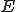 から
から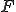 への有界線形写像
への有界線形写像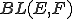 も同様にバナッハ空間である。
も同様にバナッハ空間である。
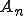 を
を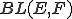 の中のコーシー列であるとする。
の中のコーシー列であるとする。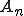 が
が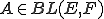 に収束することを示せばよい。
に収束することを示せばよい。
ここではまず、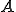 の候補として任意の
の候補として任意の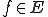 が点収束する先を選び、その後にそれが
が点収束する先を選び、その後にそれが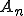 の極限なのかを調べる。
の極限なのかを調べる。
任意の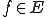 に対して
に対して
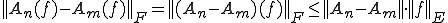
が成り立つ。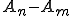 がコーシー列であったから、n,mを大きくすれば、右辺は好きなだけ小さくできる。よって
がコーシー列であったから、n,mを大きくすれば、右辺は好きなだけ小さくできる。よって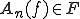 は
は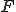 の中のコーシー列である。
の中のコーシー列である。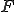 がバナッハ空間であり、完備であるから、極限
がバナッハ空間であり、完備であるから、極限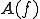 が存在して
が存在して
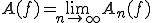
となる。よって
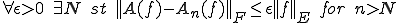
が成り立つ。この場合ノルムの定義から
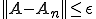
が成り立つ。これは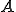 が
が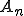 に収束することを意味している。□
に収束することを意味している。□
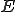 をバナッハ空間として、有界線形作用素
をバナッハ空間として、有界線形作用素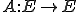 が
が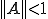 を満たすとき、
を満たすとき、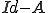 は可逆で
は可逆で
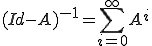
となる。
 をヒルベルト空間とする。作用素
をヒルベルト空間とする。作用素 は閾値
は閾値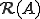 が
が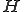 の有限次元部分空間である場合、有限次元作用素という。
の有限次元部分空間である場合、有限次元作用素という。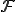 と書いた時に、ある有界線形作用素
と書いた時に、ある有界線形作用素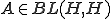 が
が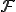 の閉包
の閉包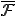 に入っていれば、完全連続作用素という
に入っていれば、完全連続作用素という
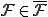 より、全ての有限次元作用素は、完全連続作用素である。
より、全ての有限次元作用素は、完全連続作用素である。
特に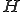 が有限次元空間である場合は、有界線形作用素と完全連続作用素であることは同値である。
が有限次元空間である場合は、有界線形作用素と完全連続作用素であることは同値である。
定義から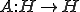 はある有限次元作用素
はある有限次元作用素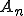 が存在して、
が存在して、
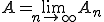
となるとき、完全連続作用素となる。
完全連続作用素は弱収束列を強収束列に写す線形写像という定義の仕方もある。つまり
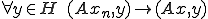
ならば
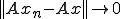
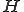 がヒルベルト空間であるとし、
がヒルベルト空間であるとし、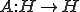 が有界完全連続作用素であるとする。また、任意の点列
が有界完全連続作用素であるとする。また、任意の点列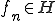 が
が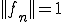 を満たすとする。このとき列
を満たすとする。このとき列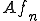 は収束する部分列を含んでいる。
は収束する部分列を含んでいる。
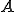 が有界完全連続作用素なので、ある有界有限次元作用素の列
が有界完全連続作用素なので、ある有界有限次元作用素の列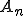 を使って、
を使って、
とできる。さて、ここで について考えよう。
について考えよう。 が有界有限次元作用素である。
が有界有限次元作用素である。
さて、 の
の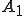 による像を
による像を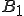 とおく。
とおく。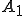 は有界で有限次元作用素であったので、
は有界で有限次元作用素であったので、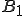 は有界で有限次元である。列
は有界で有限次元である。列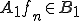 である。
である。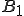 が有界で有限次元であることから、Bolzano-Weirstrausの定理を用いると、
が有界で有限次元であることから、Bolzano-Weirstrausの定理を用いると、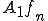 から収束する部分列を取り出すことができる。これを
から収束する部分列を取り出すことができる。これを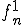 とおく。また、
とおく。また、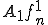 は
は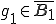 に収束するとする。
に収束するとする。
同様にして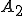 について、列
について、列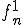 の中から、部分列
の中から、部分列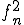 を選び、列
を選び、列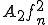 が
が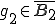 に収束できるようにできる。この処理を無限に繰り返す。つまり列
に収束できるようにできる。この処理を無限に繰り返す。つまり列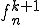 は列
は列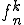 の部分列で
の部分列で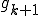 に収束するとする。
に収束するとする。
さてここでこのような列の列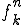 に対して
に対して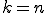 の要素に着目する。(対角線論法(diagonal procedure)という)
の要素に着目する。(対角線論法(diagonal procedure)という)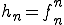 とおく。
とおく。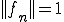 であったから、当然
であったから、当然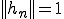 を満たす。
を満たす。
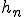 が題意の部分列であることを示そう。それには
が題意の部分列であることを示そう。それには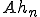 がCauchy列であることを示せばよい。
がCauchy列であることを示せばよい。
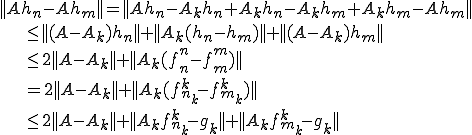
但し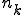 は要素
は要素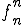 の列
の列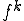 の中の位置。明らかに、
の中の位置。明らかに、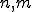 を大きくすれば、右辺は幾らでも小さくできる。したがって
を大きくすれば、右辺は幾らでも小さくできる。したがって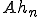 はCauchy列であり、
はCauchy列であり、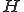 の完備性より収束する。よって題意は示された□
の完備性より収束する。よって題意は示された□
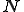 の有界線形汎関数全体を
の有界線形汎関数全体を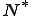 と表し、
と表し、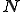 の共役空間と呼ぶ
の共役空間と呼ぶ
ノルム空間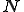 の共役空間
の共役空間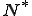 は完備である。すなわちバナッハ空間である。
は完備である。すなわちバナッハ空間である。
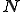 が
が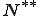 と一致するとき、回帰的(reflexive)であるという。つまり、任意の
と一致するとき、回帰的(reflexive)であるという。つまり、任意の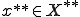 に関して
に関して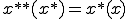
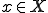 が存在する。また、
が存在する。また、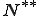 は完備であったから、回帰的なノルム空間は必ず完備である。
は完備であったから、回帰的なノルム空間は必ず完備である。
 をノルム空間とする。また、
をノルム空間とする。また、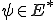 、
、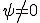 とする。このとき、ある
とする。このとき、ある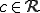 に対して、集合
に対して、集合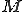
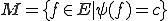
は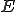 の中の閉超平面である。
の中の閉超平面である。
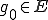 は
は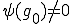 で、スケーリングによって
で、スケーリングによって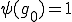 を満たすとする。
を満たすとする。
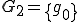 であるとする。つまり
であるとする。つまり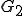 は
は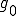 の線形倍からなる部分空間
の線形倍からなる部分空間
まず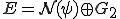 であることを示す。
であることを示す。
任意の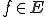 について、
について、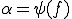 であるとすると、
であるとすると、
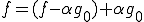
のようにかける。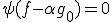 から
から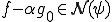 である。また明らかに
である。また明らかに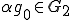 である。
である。
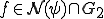 であるとすると、
であるとすると、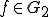 より
より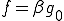 と書ける。
と書ける。
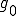 の定義から
の定義から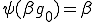 である。しかしながら
である。しかしながら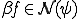 より
より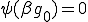 よって、
よって、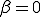 である。
である。
つまり、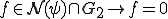
これは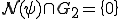 を意味している。
を意味している。
それに加えて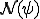 、
、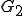 はともに閉空間である。
はともに閉空間である。
以上から、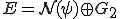 であることが示された。
であることが示された。
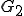 は1次元であったために、明らかに
は1次元であったために、明らかに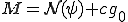 と書ける。□
と書ける。□
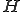 がヒルベルト空間であるとし、ある関数
がヒルベルト空間であるとし、ある関数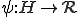 が有界線形関数であるとする。
が有界線形関数であるとする。
このとき、ある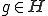 が存在して
が存在して
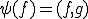
となる。さらに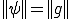 となる。
となる。
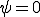 のときは
のときは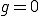 とすればよい。ここからは
とすればよい。ここからは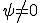 について考える。
について考える。
まず、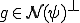 であることを示す。
であることを示す。
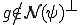 であるとすると、
であるとすると、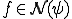 に
に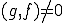 となる
となる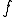 が存在する(
が存在する(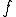 を
を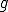 の
の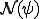 への射影ととった場合)。これは
への射影ととった場合)。これは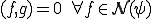 に反する。よって
に反する。よって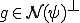
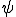 のカーネル
のカーネル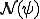 は閉空間であるから、
は閉空間であるから、
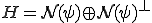
と直和分解される。上の定理より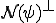 空間は1次元であった。ここで
空間は1次元であった。ここで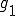 が
が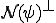 の任意の
の任意の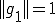 を満たす基底であるとする。ここで
を満たす基底であるとする。ここで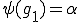 であるとする。
であるとする。
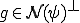 であったから、
であったから、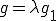 と表される。さて、
と表される。さて、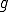 は
は
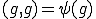
を満たさなくてはならない。つまり、
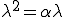
ここで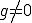 より
より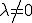 よって
よって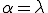 が成り立つ。以上から
が成り立つ。以上から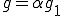
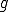 が一意に定まることが分かる。
が一意に定まることが分かる。
さて、必要条件は揃ったので、この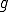 を用いて十分題意が満たされるのかを確かめてみよう。
を用いて十分題意が満たされるのかを確かめてみよう。
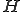 は直和分解されていたから
は直和分解されていたから
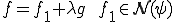
と表される。
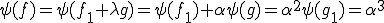
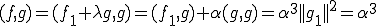
よって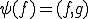
が成り立つ。以上から題意は示された□
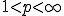 とすると、
とすると、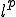 の共役空間は
の共役空間は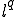 である。但し
である。但し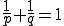
明らかに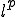 空間は回帰的である。
空間は回帰的である。
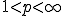 とすると、
とすると、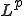 の共役空間は
の共役空間は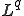 である。但し
である。但し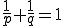
明らかに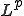 空間は回帰的である。
空間は回帰的である。
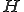 をヒルベルト空間、作用素
をヒルベルト空間、作用素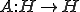 が有界であるとする。つまり、
が有界であるとする。つまり、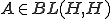
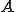 の共役作用素
の共役作用素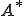 は
は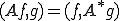
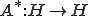 の写像である。
の写像である。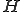 をヒルベルト空間、作用素
をヒルベルト空間、作用素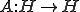 が有界であるとする。つまり、
が有界であるとする。つまり、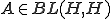
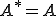
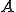 は自己共役作用素と呼ばれる。
は自己共役作用素と呼ばれる。
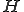 をヒルベルト空間とし、有界作用素
をヒルベルト空間とし、有界作用素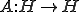 が自己共役なら
が自己共役なら
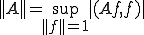
が成り立つ。
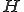 をヒルベルト空間とし、有界線形作用素
をヒルベルト空間とし、有界線形作用素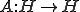 とすると、
とすると、
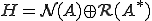
のように直和分解される。
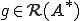 であるとする。つまり、ある
であるとする。つまり、ある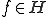 が存在して
が存在して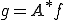 となる。
となる。
また、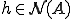 とすると、
とすると、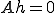 より、
より、
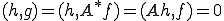
となる。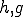 は任意であったから
は任意であったから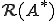 は
は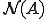 の直交補空間つまり
の直交補空間つまり
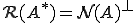
である。有界線形作用素の核空間は閉部分空間であり、閉じた部分空間とその直交補空間を用いて空間を直和分解できる。よって
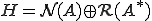
が示された□
距離空間、ノルム、線形写像、直和、零空間、作用素、ヒルベルト空間、完備、バナッハ空間
| ヒルベルト空間論 (数理物理学方法序説) |
保江邦夫 著 |