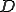 に対して、
に対して、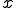 の
の -近傍(
-近傍( -neighbor)
-neighbor)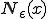 とは、
とは、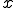 の周りの
の周りの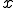 との距離が
との距離が より小さい点の集合である。つまり、
より小さい点の集合である。つまり、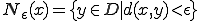
|TOP Page|
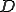 に対して、
に対して、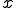 の
の -近傍(
-近傍( -neighbor)
-neighbor)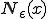 とは、
とは、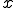 の周りの
の周りの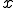 との距離が
との距離が より小さい点の集合である。つまり、
より小さい点の集合である。つまり、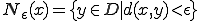
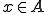 は、ある
は、ある が存在し、
が存在し、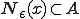 であるとき
であるとき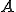 の内点(interior point)であるといわれる。
の内点(interior point)であるといわれる。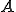 はその補集合(
はその補集合(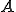 に属さない全ての点の集合)が開空間である場合、閉空間(close set)と呼ばれる。
に属さない全ての点の集合)が開空間である場合、閉空間(close set)と呼ばれる。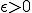 に対して、点
に対して、点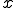 の
の 近傍、
近傍、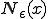 が少なくとも1つの
が少なくとも1つの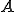 の要素を含むとき
の要素を含むとき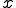 は集積点(accumulation point)と呼ばれる
は集積点(accumulation point)と呼ばれる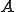 の全ての集積点の集合は
の全ての集積点の集合は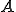 の閉包(closure)と呼ばれ
の閉包(closure)と呼ばれ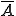 のように表される。
のように表される。
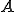 が閉空間であることと、
が閉空間であることと、
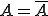
であることは同値である。
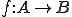 が
が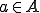 で連続であるということは
で連続であるということは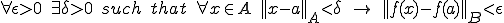
 が
が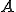 の集積点である場合は上の定義は
の集積点である場合は上の定義は
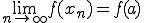
と書ける。
一次元の区間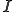 において次のように各種連続は定義される。
において次のように各種連続は定義される。
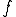 が区間
が区間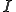 について連続であるとは、
について連続であるとは、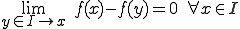 が成り立つことである。
が成り立つことである。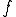 が区間
が区間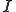 について微分可能であるということは
について微分可能であるということは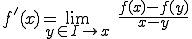 が
が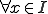 について存在するということである。
について存在するということである。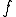 が区間
が区間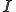 について連続に微分可能であるということは
について連続に微分可能であるということは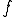 が微分可能で
が微分可能で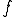 の微分
の微分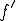 が連続であるということである。
が連続であるということである。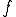 が区間
が区間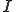 についてリプシッツ連続であるとは
についてリプシッツ連続であるとは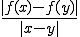 が
が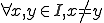 について有界であるということである。
について有界であるということである。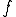 が区間
が区間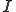 とある係数
とある係数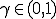 について、ヘルダー連続であるとは
について、ヘルダー連続であるとは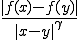 が
が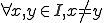 について有界であるということである。
について有界であるということである。![[a,b] [a,b]](48696C62657274205370616365_eq0055.gif) の区間的に連続な関数を
の区間的に連続な関数を![PC[a,b] PC[a,b]](48696C62657274205370616365_eq0056.gif) と表す。
と表す。区分的に連続な有界関数はリーマン積分可能である。
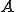 は、任意のCauchy列
は、任意のCauchy列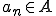 が
が の中に極限を持つとき完備であると言われる。
の中に極限を持つとき完備であると言われる。開集合は完備ではない。完備なら閉集合である。
有理数は完備ではない。反例は次のような10進数の数列、
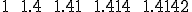
は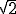 に収束するが、
に収束するが、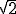 は無理数である。
は無理数である。
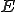 が線形空間であるとして、
が線形空間であるとして、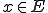 に対する
に対する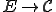 の実数関数
の実数関数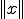 と書くとき、これが次の性質を満たせばノルムと言われる
と書くとき、これが次の性質を満たせばノルムと言われる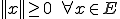 (正値性)
(正値性)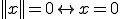
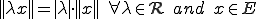 (斉次性)
(斉次性)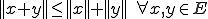 (三角不等式)
(三角不等式)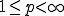 として、数列
として、数列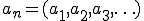 のp-ノルムは次のように定義される
のp-ノルムは次のように定義される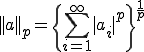
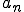 に対して∞-ノルムは次のように与えられる
に対して∞-ノルムは次のように与えられる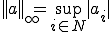
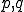 が
が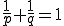 を満たすとき、数列
を満たすとき、数列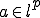 と
と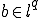 は
は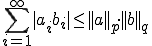
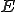 がノルム空間であるとして、
がノルム空間であるとして、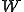 が
が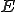 の閉部分空間であるとする。もし
の閉部分空間であるとする。もし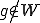 として
として
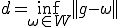
であるとする。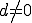 が成り立つ。なぜなら、
が成り立つ。なぜなら、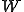 は閉部分空間であるからその補空間は開空間であり、ある
は閉部分空間であるからその補空間は開空間であり、ある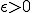 が存在して
が存在して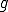 の
の -近傍に
-近傍に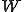 が含まれないようにできる。
が含まれないようにできる。
このとき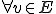 に対して、
に対して、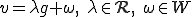 と書けるとき
と書けるとき
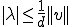
が成り立つ。なぜなら、
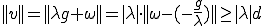
であるからである。
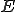 がノルム空間であるとして、
がノルム空間であるとして、 と
と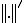 の2種類のノルムがあるとする。このとき正の実数
の2種類のノルムがあるとする。このとき正の実数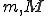 が存在して、全ての
が存在して、全ての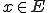 に対して
に対して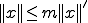
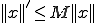
 と
と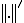 は等価なノルムであるという。
は等価なノルムであるという。
例:楕円型偏微分方程式において、エネルギーノルムと ノルムは等価なノルムである。
ノルムは等価なノルムである。
有限次元線形空間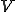 として、
として、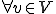 が次のように成分表示されているとする。
が次のように成分表示されているとする。
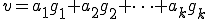
のノルムがみな次で定義されるノルム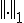 と等価であることを示す。
と等価であることを示す。
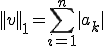
さて、ノルムと基底の係数の関係から、任意のノルム について次が成り立つ
について次が成り立つ
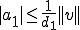
同様の操作を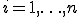 について行う。
について行う。
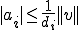
よって
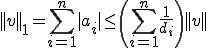
が成り立つ。また、
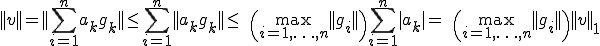
よって題意は証明された。□
完備な距離空間をバナッハ空間と呼ぶ。
有限次元の線形空間は完備である。
 を空間の次元数として、
を空間の次元数として、 についての数学的帰納法で示す。
についての数学的帰納法で示す。
(i)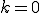 のとき明らか
のとき明らか
(ii)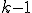 次元の線形空間が完備であるとする。この場合、
次元の線形空間が完備であるとする。この場合、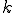 次元の線形空間
次元の線形空間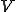 が完備であることを示す。ここで
が完備であることを示す。ここで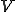 の基底が
の基底が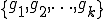 であるとする。また
であるとする。また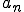 が
が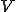 の中のCauchy列であるとしよう。
の中のCauchy列であるとしよう。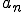 を成分表示すると、
を成分表示すると、
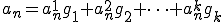
まず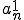 がCauchy列であることを示す。
がCauchy列であることを示す。 が
が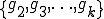 を基底とする
を基底とする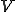 の部分空間であるとすると、帰納法の仮定から
の部分空間であるとすると、帰納法の仮定から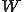 は完備である。よって
は完備である。よって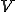 は閉じた部分空間である。上の補題よりある
は閉じた部分空間である。上の補題よりある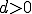 が存在して、
が存在して、
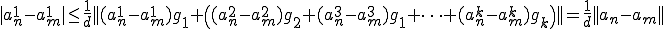
よって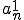 はCauchy列である。
はCauchy列である。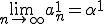 であるとする。同様の操作をおのおのの基底について行い
であるとする。同様の操作をおのおのの基底について行い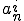 の極限を
の極限を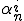 とする。
とする。
次に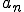 の極限
の極限 が
が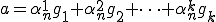 と表されることを示す。
と表されることを示す。
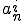 の収束より、任意の
の収束より、任意の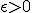 について、ある
について、ある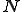 が存在し、
が存在し、
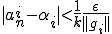
が全ての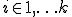 と
と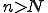 について成り立つ。これを用いると
について成り立つ。これを用いると
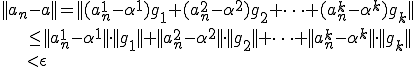
となる。よって極限が存在するので は完備
は完備
以上から有限次元の線形空間が完備であることが分かる□
有限要素法ではRitz-Galerkin法を用いて、エネルギーノルムにおける有限要素法離散化空間内で弱解の最良近似を求める。有限要素法離散化空間は有限次元の空間であるので完備である。これを用いると弱解の最良近似は常に存在することがわかる。
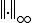 は
は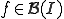 について、
について、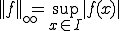
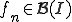 が、ある関数
が、ある関数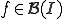 に一様収束するとは
に一様収束するとは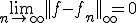
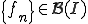 は、極限
は、極限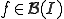 が全ての
が全ての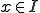 に対して
に対して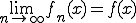
一様収束すれば点収束するこをを示す。
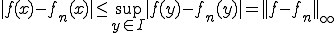
であるから、一様収束すれば点収束する。
区間![[0,1] [0,1]](48696C62657274205370616365_eq0163.gif) において、
において、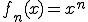 は
は
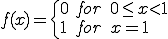
に点収束するが、一様収束はしない。なぜなら常に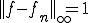 であるからである。
であるからである。
一様収束は点収束よりも強い意味での収束であることがいえる。
有界関数が一様ノルムで完備であることを示すためには、有界関数の列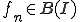 がCauchy列であれば有界関数に一様収束することを示せばよい。
がCauchy列であれば有界関数に一様収束することを示せばよい。
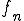 がCauchy列であるとする。すなわち、
がCauchy列であるとする。すなわち、
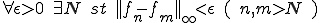
任意の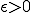 について、ある
について、ある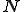 が存在して
が存在して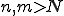 について、
について、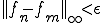 となる。
となる。
ここで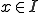 について
について
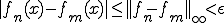
が成り立つので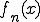 はCauchy列である。
はCauchy列である。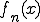 の収束先を
の収束先を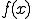 とする。つまり
とする。つまり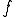 は
は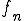 の点収束先
の点収束先
さて、上の不等式の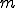 を固定したまま、
を固定したまま、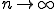 を計算すると
を計算すると
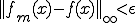
となる。これが任意の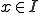 について成り立つので
について成り立つので
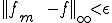
つまり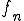 は
は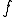 に一様収束しているということが言える。また、ある
に一様収束しているということが言える。また、ある について、
について、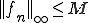 が成り立つとき、上から
が成り立つとき、上から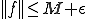 がいえる。よって一様収束する先は有界関数
がいえる。よって一様収束する先は有界関数
以上から有界関数が完備であることが示された□
Bolzano-Weirstrausの定理から[a,b]で定義される連続関数は全て有界である。つまり
![C[a,b]\sub B[a,b] C[a,b]\sub B[a,b]](48696C62657274205370616365_eq0191.gif)
が成り立つ。
上から、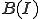 は完備であったから、
は完備であったから、![C[a,b] C[a,b]](48696C62657274205370616365_eq0193.gif) のCauchy列は
のCauchy列は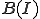 に収束する。よって、収束した先が連続であることを証明すれよい。
に収束する。よって、収束した先が連続であることを証明すれよい。
関数列![f_n\in C[a,b] f_n\in C[a,b]](48696C62657274205370616365_eq0195.gif) とする。
とする。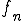 が一様収束する先を
が一様収束する先を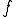 としよう。さて、
としよう。さて、![x,x_0\in [a,b] x,x_0\in [a,b]](48696C62657274205370616365_eq0198.gif) に対して、
に対して、
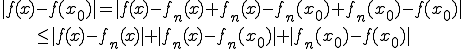
が成り立つ。
さて、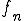 は連続関数であったので、
は連続関数であったので、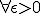 に対して、
に対して、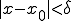 なら
なら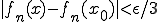 であるような
であるような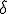 が存在する。
が存在する。
また、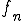 は
は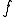 に一様収束するので、
に一様収束するので、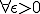 に対して、
に対して、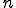 が十分大きければ
が十分大きければ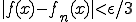 、
、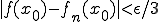 となる。
となる。
以上から
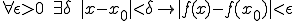
であるといえる。つまり は連続関数
は連続関数
よって題意は証明された□
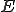 が
が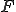 の部分空間であり、
の部分空間であり、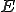 の閉包が
の閉包が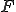 である、つまり
である、つまり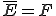 であるとき、
であるとき、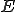 は
は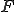 の中で稠密であるという。
の中で稠密であるという。
有理数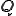 は実数
は実数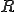 の中で稠密である。
の中で稠密である。
整数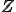 は実数
は実数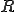 の中で稠密ではない。
の中で稠密ではない。
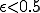 のとき、
のとき、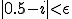 を満たすような
を満たすような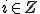 が存在しない。
が存在しない。
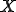 が
が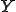 の中で稠密であるとする。ある連続関数
の中で稠密であるとする。ある連続関数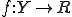 が
が
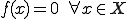
を満たすなら、
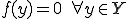
が成り立つ。
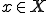 、
、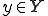 であるとする。
であるとする。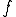 が連続関数であったから、
が連続関数であったから、
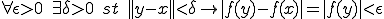
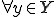 について
について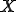 が
が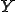 で稠密であったから、
で稠密であったから、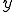 に収束する列
に収束する列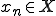 が存在する。つまり、上の
が存在する。つまり、上の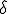 に対して、ある自然数
に対して、ある自然数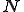 が存在して
が存在して
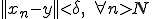
となる。つまり、どんな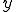 にたいしても
にたいしても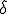 より距離の近い
より距離の近い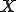 の要素が存在する。
の要素が存在する。
以上より、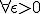 に対して
に対して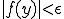 とすることができる。つまり
とすることができる。つまり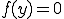 □
□
これは、もし稠密な部分空間である連続的なことが成り立つことは全空間で成立つことを示している。
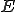 が
が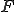 の中で稠密であるとき、
の中で稠密であるとき、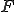 の任意の元
の任意の元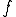 に対して、
に対して、
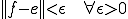
となるような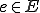 が存在する。
が存在する。
これはFの任意の元はEの元によって任意の精度で近似することができるということを表している。
例えば、無理数は小数で近似することができる。
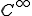 級関数は
級関数は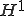 空間で稠密であることを用いて、有限要素法の妥当性がいえる。
空間で稠密であることを用いて、有限要素法の妥当性がいえる。
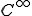 級関数は微分が区分連続な連続関数の空間の部分空間であるから、微分が区分連続な連続関数の空間も
級関数は微分が区分連続な連続関数の空間の部分空間であるから、微分が区分連続な連続関数の空間も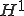 空間の中で稠密であるといえる。
空間の中で稠密であるといえる。
変分原理から導かれる弱解は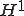 空間中にあり、エネルギーノルムと
空間中にあり、エネルギーノルムと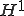 ノルムは微分方程式の楕円性により等価である。つまり、弱解は微分が区分連続な連続関数によってエネルギーノルムで任意の精度で近似することができる。
ノルムは微分方程式の楕円性により等価である。つまり、弱解は微分が区分連続な連続関数によってエネルギーノルムで任意の精度で近似することができる。
エネルギーノルムにおける離散空間中での弱解の最良近似が有限要素法解である。メッシュを好きなだけ細かくすることができれば、有限要素法を使ってエネルギーノルムや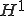 ノルムで弱解を任意の精度で近似することができることがわかる。
ノルムで弱解を任意の精度で近似することができることがわかる。
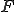 が完備であり、
が完備であり、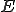 が
が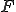 の中で稠密であるとき
の中で稠密であるとき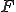 は
は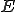 を完備化(completion)したものと呼ばれる。
を完備化(completion)したものと呼ばれる。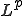 ノルム
ノルム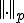 ノルムとは、
ノルムとは、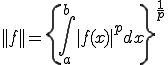
 とする。
とする。 空間は完備
空間は完備![C[a,b] C[a,b]](48696C62657274205370616365_eq0273.gif) 空間は
空間は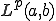 空間の中で稠密。よって
空間の中で稠密。よって![C[a,b] C[a,b]](48696C62657274205370616365_eq0275.gif) を
を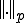 ノルムを用いて完備化したものは
ノルムを用いて完備化したものは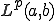 である。
である。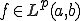 、
、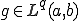 であり、
であり、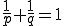 であるとする。
であるとする。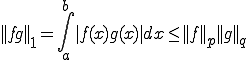
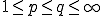 であるとき、
であるとき、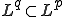 を満たす。
を満たす。
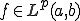 とする。
とする。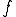 に依存しないある正の定数
に依存しないある正の定数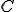 が存在して、
が存在して、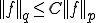 であるとことを示せばよい。
であるとことを示せばよい。
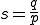 と置き、Hölderの不等式に
と置き、Hölderの不等式に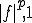 を代入する。
を代入する。
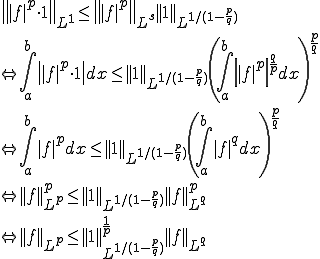
よって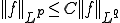 が成立つ。このことから
が成立つ。このことから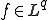 であれば
であれば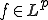 である。つまり、
である。つまり、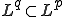 □
□
前に連続関数![C[a,b] C[a,b]](48696C62657274205370616365_eq0295.gif) は
は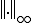 ノルムで完備であることを述べたが、
ノルムで完備であることを述べたが、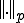 ノルムでは連続関数は完備ではない
ノルムでは連続関数は完備ではない
反例は次のような関数列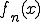 によって与えられる。
によって与えられる。
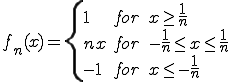
この関数がCauchy列であることを示し、極限が連続関数でないことを示す。
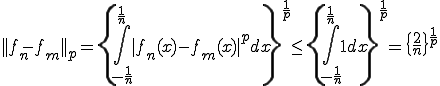
よって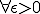 について、
について、 とすれば
とすれば
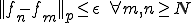
となる。よって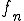 はCauchy列となる。しかしながら、
はCauchy列となる。しかしながら、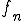 の極限
の極限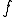 は
は
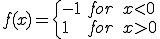
である。これは連続関数ではない。よって連続関数は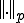 ノルムで完備では無い。
ノルムで完備では無い。
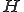 は、
は、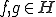 について
について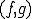 で表されるような実数が存在して、次の性質を満たすとき内積空間と呼ばれる。
で表されるような実数が存在して、次の性質を満たすとき内積空間と呼ばれる。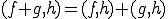
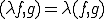
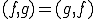
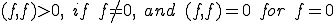
内積空間の中の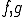 について、
について、
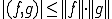
が成り立つ。
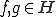 について、
について、
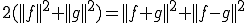
が成り立つ。
あるノルム空間にが内積空間である必要十分条件は、中線定理が成り立つことである。
このとき、内積は
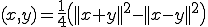
と定義される。
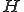 をノルム空間とし、
をノルム空間とし、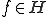 、
、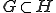 とする。
とする。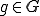 は次のとき
は次のとき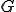 の中の
の中の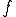 の最良近似(best approximation)と言われる
の最良近似(best approximation)と言われる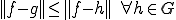
注意すべきことはノルム空間では最良近似は一意でないということ。
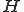 が内積空間であるとし、
が内積空間であるとし、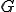 は
は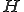 の線形部分空間、
の線形部分空間、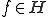 とする。次このとき、次の2つは同値
とする。次このとき、次の2つは同値
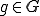 について、
について、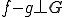 が成り立つ
が成り立つ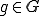 は
は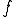 の最良近似
の最良近似また、最良近似が存在するとき、それは一意である(一般的なノルムの場合と違って、内積から作られるノルムに対しては一意である)
1→2
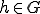 とすると、
とすると、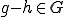 よって、
よって、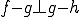
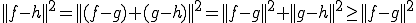
よって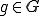 は最良近似
は最良近似
2→1
背理法で示す.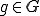 が
が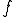 の最良近似であるとき、
の最良近似であるとき、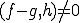 であるような
であるような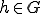 が選べたとする.
が選べたとする.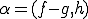 として、
として、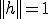 となるように
となるように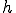 が正規化されているとする.このとき、
が正規化されているとする.このとき、
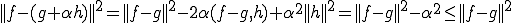
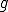 は最良近似ではないので矛盾.よって、
は最良近似ではないので矛盾.よって、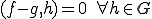 となる.□
となる.□
一意性については、
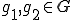 が
が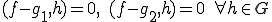 を満たすとすると、
を満たすとすると、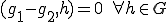 が成り立つ.
が成り立つ.
ここで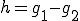 と選ぶと
と選ぶと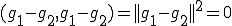 より、
より、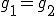 となる.よって最良近似が存在するならば、一意に定まる.
となる.よって最良近似が存在するならば、一意に定まる.
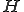 が内積空間で
が内積空間で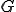 が完備な線形部分空間である場合、任意の
が完備な線形部分空間である場合、任意の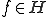 に対して最良近似
に対して最良近似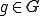 が存在する。
が存在する。
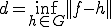 とおく.
とおく.
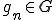 を
を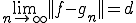 となるような数列であるとする.
となるような数列であるとする.
このとき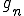 がCauchy列であることを証明する.
がCauchy列であることを証明する.
ここで、
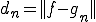 とおく.中線定理を用いると、
とおく.中線定理を用いると、
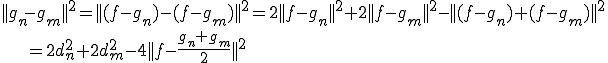
となる.ここで、Gは線形空間であるから、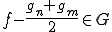 である.
である.
よって、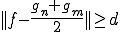 となる.以上から
となる.以上から
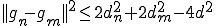
となる.
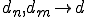
であるから、n,mを十分大きく取れば、任意の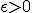 に対して
に対して
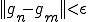
となるようにすることができる.よって、
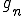 はCauchy列である.
はCauchy列である.
よって、Gは完備であるから、
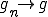 となるような
となるような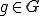 が存在する.□
が存在する.□
距離空間、ノルム、線形写像、直和、零空間、作用素、ヒルベルト空間、完備、バナッハ空間
| ヒルベルト空間論 (数理物理学方法序説) |
保江邦夫 著 |