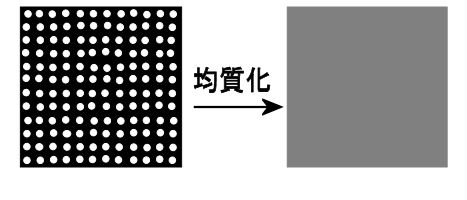
|TOP Page|
均質化とは非均質な構造物が周期性を持つ微視構造によって構成されているという場合に、等価である均質な材料物性の値を求める方法である。
微小な周期性を持つ構造物の解析の他にも、形状最適化において制約条件に起因する不安定性を緩和する手法の一つとしても広く用いられている[1]。
均質化法の歴史についてはこちらのページが詳しい
簡単のため1次元のバネを使って均質化法の概念を説明する。
直列につないだバネ1,2とする。この剛性バネのバネ定数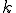 を求めてみよう。
を求めてみよう。
バネを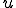 だけ引っ張ったときに力
だけ引っ張ったときに力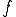 が発生したとする。
が発生したとする。
力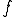 の元で、バネ1,2はそれぞれ、
の元で、バネ1,2はそれぞれ、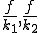 だけ伸ばされるから全体の変位
だけ伸ばされるから全体の変位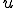 は
は
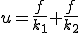
と表される。直列バネのバネ定数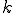 は変位と力の比なので、
は変位と力の比なので、
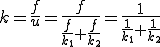
と表すことができる。
直列の場合、合成ばね定数は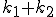 とならないことに注意しよう。このことは均質化法の概念として後々重要になってくる。
とならないことに注意しよう。このことは均質化法の概念として後々重要になってくる。
さらに、長さ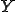 のバネを考えてみよう。このバネは2種類のバネ1,2が直列につながって出来ていて、それぞれ、単位長さあたりの伸びとと力の比が
のバネを考えてみよう。このバネは2種類のバネ1,2が直列につながって出来ていて、それぞれ、単位長さあたりの伸びとと力の比が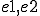 であるとする。また、長さ
であるとする。また、長さ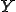 の中で割合としてそれぞれ、
の中で割合としてそれぞれ、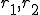 だけを占めているとする。
だけを占めているとする。
バネ1、2のバネ定数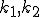 はそれぞれ、
はそれぞれ、
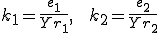
となる。上の例を用いて、この長さ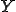 のバネ定数
のバネ定数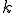 は次のようになる。
は次のようになる。
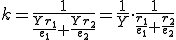
と表される。これは、単位長さあたりの伸びと力の比 が
が
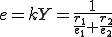
の均質なバネのバネ定数に等しい。
単純なバネの合成の平均でないことに注意したい。つまり
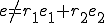
例えば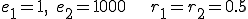 の場合は
の場合は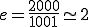 となる。常に小さい値が大きく影響する。
となる。常に小さい値が大きく影響する。
このバネが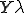 だけ引き伸ばされたときの、左端を基点とする変位の関数
だけ引き伸ばされたときの、左端を基点とする変位の関数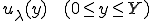 を求めてみよう。
を求めてみよう。
力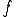 は
は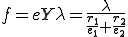 だけ発生する。
だけ発生する。
バネ1,2の単位あたりの伸び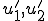 は、それぞれ、
は、それぞれ、
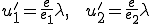
である。したがって変位の関数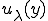 は次のとおり、
は次のとおり、
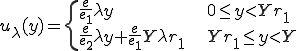
さて、この2種類のバネがつながったバネがの長さを係数 を用いて調整できるとする。つまり、長さが
を用いて調整できるとする。つまり、長さが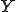 だったバネが
だったバネが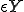 の長さであるとする。さらに、このバネが直列に沢山つながっていて、周期的構造を持っているとしよう。全体の長さが
の長さであるとする。さらに、このバネが直列に沢山つながっていて、周期的構造を持っているとしよう。全体の長さが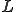 であるとき、バネは
であるとき、バネは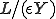 個だけつながっていることになる。
個だけつながっていることになる。
1つ1つのバネをユニットセルと呼ぶ。
1つ1つのバネのバネ定数は
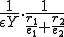
と表される。これが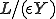 個だけつながっているとすると、全体のバネ定数
個だけつながっているとすると、全体のバネ定数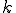 は
は
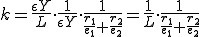
と表される。 が0の極限をとるとき、このバネは均質であるとみなすことができるだろう。このとき、単位長さあたりの伸びと力の比
が0の極限をとるとき、このバネは均質であるとみなすことができるだろう。このとき、単位長さあたりの伸びと力の比 は、
は、
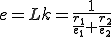
と表されることになる。単位長さあたりの伸びと力の比はεの値によらず一定であることが分かる。よって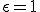 、つまり長さ
、つまり長さ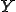 の場合の単位長さの伸びと力の比を考えればよいことが分かる。このようにして、長さ
の場合の単位長さの伸びと力の比を考えればよいことが分かる。このようにして、長さ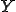 のモデルになんらかの形で等価な均質なモデルを考えることで、無限にユニットセルが小さくなったときの値を求めることができる。
のモデルになんらかの形で等価な均質なモデルを考えることで、無限にユニットセルが小さくなったときの値を求めることができる。
さて、この周期構造を持つ長さ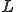 のバネを
のバネを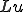 だけ伸ばしたとしよう。バネを引き伸ばしたときの左端を基点とした変位を
だけ伸ばしたとしよう。バネを引き伸ばしたときの左端を基点とした変位を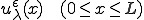 と置く。
と置く。
1つ1つのバネは
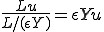
だけ伸ばされていることになる。よって、このユニットセル内の変形を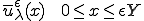 と表すと、
と表すと、
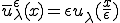
となることが分かる。
さて、次のような関数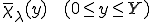 を考えよう
を考えよう
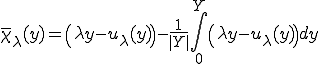
この関数は
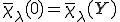
を満たすように線形成分を取り除き次のように平均を0にするために定数成分を調整したものである。
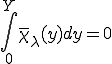
Yの基本構造の変位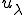 は次のように表すことができる。
は次のように表すことができる。
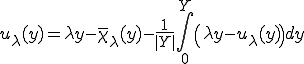
さて、この関数をつなげて、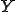 周期性を持たせた関数を
周期性を持たせた関数を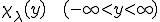 とする。つまり、
とする。つまり、
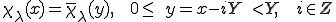
この関数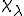 は特性関数と呼ばれる。特性関数はマクロな変形
は特性関数と呼ばれる。特性関数はマクロな変形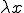 に対するミクロな応答である。
に対するミクロな応答である。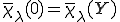 を満たすことから、特性変形は連続関数である。
を満たすことから、特性変形は連続関数である。
関数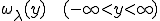 を
を
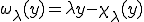
のように定義する。
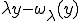
は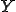 周期的であることが分かる。
周期的であることが分かる。
さて、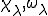 をスケーリングした関数、
をスケーリングした関数、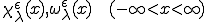 を次のように定義する。
を次のように定義する。
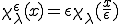
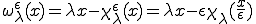
この特性変形を使って変位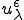 は次のように分解することができる。
は次のように分解することができる。
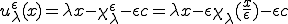
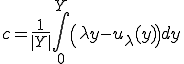
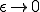 のとき、
のとき、
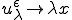
であることがわかる。
勾配は
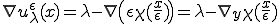
と表される。
勾配は各点ではλに収束しないが、平均化したものはλに収束している
このような平均した収束の概念は弱収束を使って表現することができる。
多次元の例として異方性を持ったポアソン方程式を扱う。
ここで、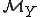 は
は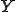 における平均を表していて、
における平均を表していて、
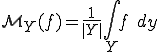
である。ここで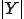 はユニットセルの体積ないし面積である。
はユニットセルの体積ないし面積である。
次のポアソン方程式を均質化する。
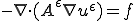 、
、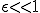
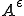 はスケーリングパラメータ
はスケーリングパラメータ を使い、
を使い、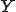 周期性を持っている係数行列
周期性を持っている係数行列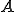 の周期を短くしたものであり、
の周期を短くしたものであり、
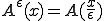
を満たす。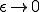 の時に、
の時に、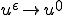 となる
となる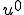 が、
が、
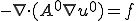
を解けば求まるような、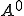 を求めるのが目的である。
を求めるのが目的である。
このような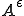 から
から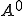 への収束はH-収束と呼ばれる。
への収束はH-収束と呼ばれる。
マクロの変形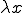 が与えられたときのユニットセルの変形
が与えられたときのユニットセルの変形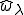 を考えよう。平衡状態の式は次のとおり。
を考えよう。平衡状態の式は次のとおり。
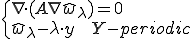
これは次のように弱形式化される。
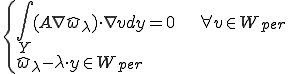
さて、マクロな変形からユニットセルの変形を取り除いたミクロな周期的な変位、つまり特性関数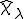 を求めてみよう。
を求めてみよう。
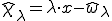
を代入して、
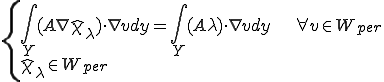
となる。
Tartarの定理より均質化された係数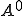 は
は
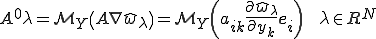
によって与えられる。
さて、次のように転置された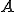 に対するユニットセル内の平衡方程式を満たす変位を
に対するユニットセル内の平衡方程式を満たす変位を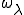 とする
とする
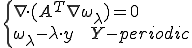
これは次のように弱形式化される。
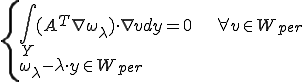
さて、マクロな変形からユニットセルの変形を取り除いたミクロな周期的な変位、つまり特性関数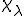 を求めてみよう。
を求めてみよう。
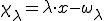
を代入して、
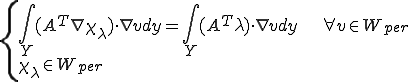
となる。この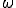 を用いて
を用いて
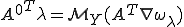
と書くことができる。これは均質化した係数行列の転置と、係数行列の転置を均質化したものが等しいことを表している。つまり、
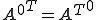
行列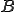 を
を
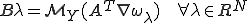
を満たす行列であるとしたときに、
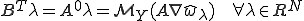
を示せばよい。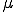 を
を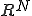 の任意の要素であるとする。
の任意の要素であるとする。
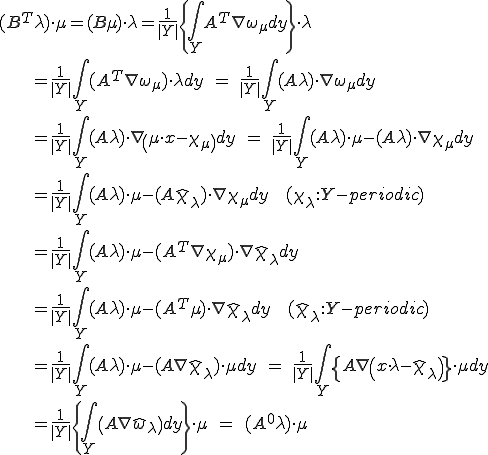
任意の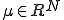 について
について
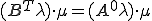
が成り立つので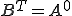 が成り立つ。□
が成り立つ。□
上の均質化法の式は漸近展開(asymptotic expansion)を用いることで比較的簡単に確認できる。
次のように漸近展開できるとする。
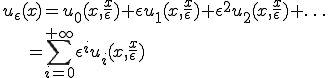
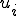 の微分は次のようになる
の微分は次のようになる
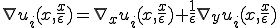
但し、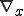 はマクロスケール、
はマクロスケール、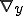 はミクロスケールの微分を表す。
はミクロスケールの微分を表す。
これを上式に代入すると
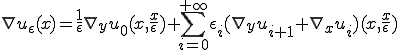
となる。さて、これをポアソン方程式に代入してみよう
\\ -\frac{1}{\epsilon} \[\nabla_y\cdot \(A\nabla_x u_0+A\nabla_y u_1\)+\nabla_x\cdot\(A\nabla_y u_0\)\] (x,\frac{x}{\epsilon})\\ -\[\nabla_x\cdot(A\nabla_x u_0+A\nabla_y u_1)+\nabla_y\cdot(A\nabla_x u_1+A\nabla_y u_2)\](x,\frac{x}{\epsilon})\\ -\sum^{\infty}_{i=1}\epsilon^i\[\nabla_x\cdot(A\nabla_x u_i+A\nabla_y u_{i+1})+\nabla_y\cdot(A\nabla_x u_{i+1}+A\nabla_y u_{i+2})\](x,\frac{x}{\epsilon})\\=f(x) -\frac{1}{\epsilon^2}\[\nabla_y\cdot \(A\nabla_y u_0\)\](x,\frac{x}{\epsilon})\\ -\frac{1}{\epsilon} \[\nabla_y\cdot \(A\nabla_x u_0+A\nabla_y u_1\)+\nabla_x\cdot\(A\nabla_y u_0\)\] (x,\frac{x}{\epsilon})\\ -\[\nabla_x\cdot(A\nabla_x u_0+A\nabla_y u_1)+\nabla_y\cdot(A\nabla_x u_1+A\nabla_y u_2)\](x,\frac{x}{\epsilon})\\ -\sum^{\infty}_{i=1}\epsilon^i\[\nabla_x\cdot(A\nabla_x u_i+A\nabla_y u_{i+1})+\nabla_y\cdot(A\nabla_x u_{i+1}+A\nabla_y u_{i+2})\](x,\frac{x}{\epsilon})\\=f(x)](6261736973206F6620486F6D6F67656E697A6174696F6E204D6574686F6473_eq0132.gif)
さて、漸近展開法ではパラメータ に関する項について右辺左辺が等しいという条件を使って
に関する項について右辺左辺が等しいという条件を使って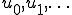 を求める。実際これらは以下のようになる。
を求める。実際これらは以下のようになる。
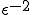 の項に着目しよう。
の項に着目しよう。
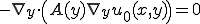
これは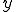 についてのみの方程式である。これは
についてのみの方程式である。これは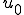 が
が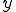 によらない関数であること
によらない関数であること
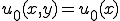
を示している。よって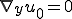
つまり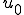 は周期的な変形をしない、滑らかな関数である。
は周期的な変形をしない、滑らかな関数である。
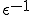 の項に着目しよう。
の項に着目しよう。
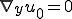 を代入すると、
を代入すると、
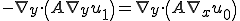
となる。これは、ミクロの周期変形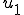 は、
は、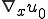 と線形な関係にあることをを表している。
と線形な関係にあることをを表している。
ここで、一次独立なベクトル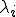 に対応する周期変形モードを
に対応する周期変形モードを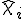 とする。つまり、
とする。つまり、
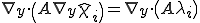
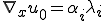
と分解するとき、
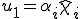 と表される。
と表される。
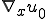 から
から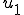 への変換行列を
への変換行列を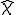 と書くことにする。つまり、
と書くことにする。つまり、
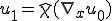
変形モード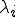 として正規直交基底
として正規直交基底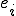 を用いると、
を用いると、
![\hat{\chi}=\[\hat{\chi}_1,\hat{\chi}_2,\hat{\chi}_3\] \hat{\chi}=\[\hat{\chi}_1,\hat{\chi}_2,\hat{\chi}_3\]](6261736973206F6620486F6D6F67656E697A6174696F6E204D6574686F6473_eq0159.gif)
と簡単に書ける
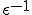 の項つまり定数項に着目しよう。
の項つまり定数項に着目しよう。
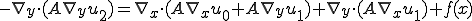
さて、上の式をユニットセルで積分して平均する。ここで、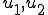 は周期的であるから、
は周期的であるから、
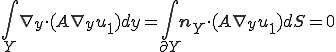
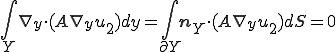
が成り立つことに注意しよう。このとき、
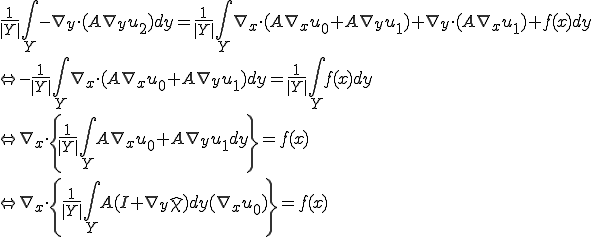
ここで、
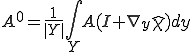
とすると、最終的に
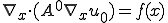
を解くことでマクロ変形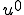 が求まる。
が求まる。
均質化の正当性について示すには数学、特に関数解析の知識が必要である。特に重要な式を以下に挙げる。
ある列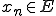 が
が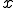 に強く収束するとは
に強く収束するとは
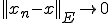
であることをいう。
ある列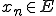 は次のようなとき
は次のようなとき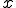 に弱く収束する(Converge Weakly)と言われる。
に弱く収束する(Converge Weakly)と言われる。
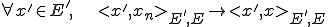
このような場合次のように書かれる
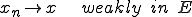
このような弱い収束は平均的な意味での収束という意味がある。
強く収束するなら、弱く収束する。なぜなら、
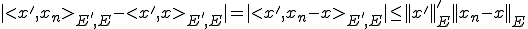
であるかあら、強く収束する場合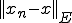 は任意に小さくできるので、
は任意に小さくできるので、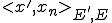 を
を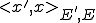 に任意に近づけることができるからである。
に任意に近づけることができるからである。
点列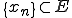 、
、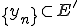 がそれぞれ次のように収束するとする。
がそれぞれ次のように収束するとする。
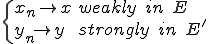
このとき、
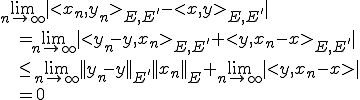
よって
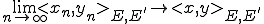
となる。
ソボレフの埋蔵定理より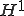 空間は
空間は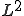 空間にコンパクトに埋め込まれる。よって
空間にコンパクトに埋め込まれる。よって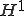 空間での弱収束する列は、
空間での弱収束する列は、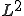 空間での強収束する。
空間での強収束する。
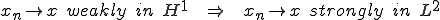
 が
が 周期的な関数
周期的な関数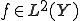 であるとする。次のように
であるとする。次のように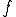 をパラメータ
をパラメータ を使ってスケーリングしたものを
を使ってスケーリングしたものを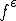 とする。
とする。
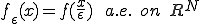
このとき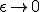 で
で
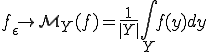 weakly in
weakly in 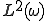
となる。
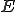 が再帰的で
が再帰的で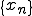 が
が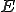 の中の有界な列であるとする。
の中の有界な列であるとする。
ある列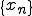 の部分列
の部分列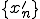 と
と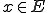 が存在し、
が存在し、
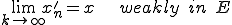
となる。また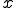 が一意に定まるとき、
が一意に定まるとき、
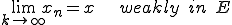
となる。
証明は[Functional Analysis, Kosaku Yosida p141]を参考されたい。
さて、 でスケーリングしたユニットセルの
でスケーリングしたユニットセルの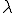 に対する応答変位を
に対する応答変位を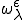 とする。
とする。
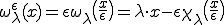
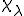 は
は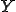 周期的で、
周期的で、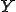 平均が0であるからすぐに次が満たされる
平均が0であるからすぐに次が満たされる
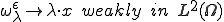
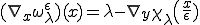
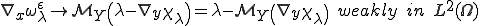
グリーン・ガウスの定理からが成り立つ。
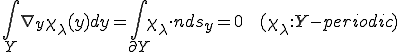
よって
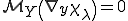
結局上から
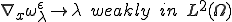
が成り立つ。つまり、
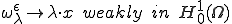
ソボレフの埋蔵定理から、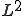 空間は
空間は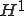 空間でコンパクトである。よって、
空間でコンパクトである。よって、
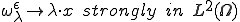 |
が成り立つ。
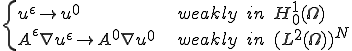
但し、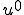 は
は
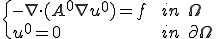
の解で、正定値対称の行列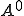 は次のように与えられる。
は次のように与えられる。
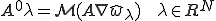
係数行列の転置に関する式から、
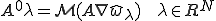
と
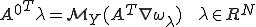
は等価であった。
下式を示せば上式を示したことになる。ここでは転置に関する均質化である下式を示す。証明は[Introduction to Homogenization, Doina Cioranescu and Patrizia Donato, chap8]を大幅に参考にした。
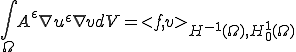
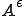 は楕円的。つまり
は楕円的。つまり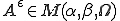
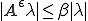
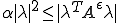
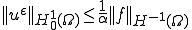
よって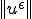 は有界列であることがわかる。
は有界列であることがわかる。
ある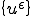 の部分列
の部分列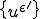 と
と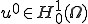 が存在して
が存在して
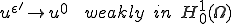 |
となる。また、ソボレフの埋蔵定理より
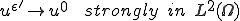 |
となる。ここで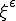 を次のように定義しよう。
を次のように定義しよう。
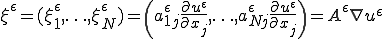
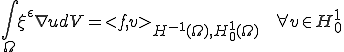
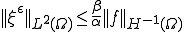
よってある部分列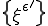 と
と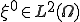 が存在して
が存在して
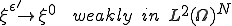 |
となる。弱収束の定義から
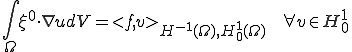 |
を満たすこれは
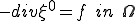
を満たすことを意味している。
![\eta^\epsilon_\lambda(x)=\frac{1}{\epsilon}\[A^T\(\frac{x}{\epsilon}\)\(\nabla_y\(\epsilon \omega_\lambda \)\)\(\frac{x}{\epsilon}\)\]=(A^T\nabla_y \omega_\lambda)\(\frac{x}{\epsilon}\) \eta^\epsilon_\lambda(x)=\frac{1}{\epsilon}\[A^T\(\frac{x}{\epsilon}\)\(\nabla_y\(\epsilon \omega_\lambda \)\)\(\frac{x}{\epsilon}\)\]=(A^T\nabla_y \omega_\lambda)\(\frac{x}{\epsilon}\)](6261736973206F6620486F6D6F67656E697A6174696F6E204D6574686F6473_eq0254.gif)
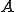 が
が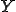 周期的で
周期的で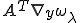 が
が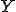 周期的だから細かく振動する周期関数の弱収束に関する定理を使って
周期的だから細かく振動する周期関数の弱収束に関する定理を使って
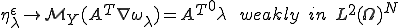 |
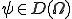
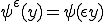
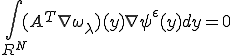
さて、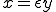 をここに代入して、
をここに代入して、
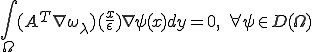
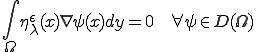 |
が成り立つ。
応力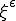 の弱形式の平衡方程式のテスト関数
の弱形式の平衡方程式のテスト関数 に
に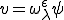 を代入して、
を代入して、
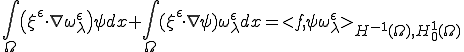
また、特性変形によって発生する周期的応力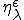 の弱形式による釣り合いの式のテスト関数
の弱形式による釣り合いの式のテスト関数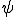 に
に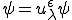 を代入して
を代入して
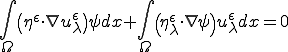
が成り立つ。応力と特性変形の勾配の内積は、特性変形による応力と変形の勾配と等しい。
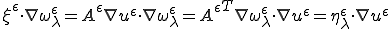
上式から下式を引いて次を得る。
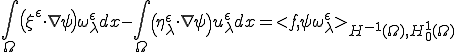
上の定理より強収束するものと弱収束するものの内積は弱収束するのであった。
ここで、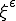 は
は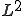 で弱収束、
で弱収束、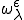 は
は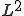 で強収束なので以下が成り立つ。
で強収束なので以下が成り立つ。
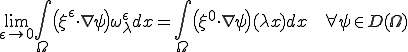
同様にして、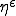 は
は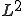 で弱収束、
で弱収束、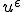 は
は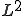 で強収束なので以下が成り立つ。
で強収束なので以下が成り立つ。
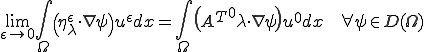
これらを上の式に代入すると次を得る。
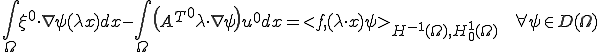
書き換えると
![\int_\Omega \xi^0\cdot\nabla[(\lambda x)\psi] dx - \int_\Omega \(\xi^0\cdot\lambda\) \psi dx - \int_\Omega\({A^T}^0\lambda\cdot\nabla\psi\) u^0 dx = <f,(\lambda\cdot x)\psi>_{H^{-1}(\Omega),H^1_0(\Omega)}\;\;\forall\psi\in D(\Omega) \int_\Omega \xi^0\cdot\nabla[(\lambda x)\psi] dx - \int_\Omega \(\xi^0\cdot\lambda\) \psi dx - \int_\Omega\({A^T}^0\lambda\cdot\nabla\psi\) u^0 dx = <f,(\lambda\cdot x)\psi>_{H^{-1}(\Omega),H^1_0(\Omega)}\;\;\forall\psi\in D(\Omega)](6261736973206F6620486F6D6F67656E697A6174696F6E204D6574686F6473_eq0287.gif)
テスト関数に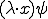 を代入して
を代入して
![\int_\Omega \xi^0\cdot\nabla[(\lambda x)\psi] dx = <f,(\lambda\cdot x)\psi>_{H^{-1}(\Omega),H^1_0(\Omega)}\;\;\forall\psi\in D(\Omega) \int_\Omega \xi^0\cdot\nabla[(\lambda x)\psi] dx = <f,(\lambda\cdot x)\psi>_{H^{-1}(\Omega),H^1_0(\Omega)}\;\;\forall\psi\in D(\Omega)](6261736973206F6620486F6D6F67656E697A6174696F6E204D6574686F6473_eq0289.gif)
これを上に代入すると
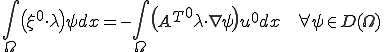
となる。ここで、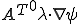 は定数であったので、
は定数であったので、
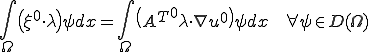
が成り立つ。以上から
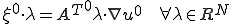 |
が成り立つことがわかる。
上式の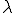 は任意であったので、
は任意であったので、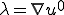 を代入して領域
を代入して領域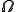 で積分すると、
で積分すると、
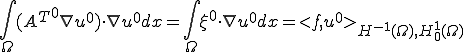
が成り立つ。Lax-Milgramの定理から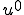 は
は
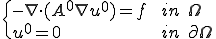
の解で、一意に存在することが分かる。よって題意は証明された□
全体の歪エネルギー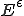 は
は
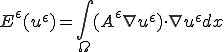
のように書くことができる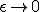 のとき
のとき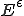 は次のような
は次のような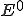 に収束する。
に収束する。
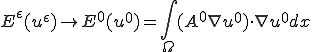
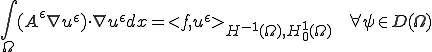
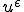 は
は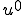 に収束するので、
に収束するので、
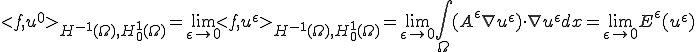
となる。一方
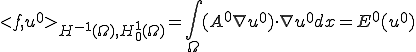
であるから、
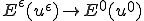
が成り立つ。
[1]Bendsøe,M.P. and Kikuchi, N.:Generating optimal topologies in structural design using a homogenization method, Comp. Meths. Appl. Mechs. Engng., Vol. 71, pp.197-224
[2]Non-Homogeneous Media and Vibration Theory, Edited by Enrique Sanchez-Palencia, Lecture Notes in Physics, vol. 127
| 均質化法入門- 計算力学レクチャーシリーズ- | 寺田賢二郎 著 |
| An Introduction to Homogenization | Doina Cioranescu, Patrizia Donato 著 |
| Shape Optimization by the Homogenization Method | Gregoire Allaire 著 |
| Functional Analysis | Kosaku Yosida 著 |