

|TOP Page|
熱が時間とともに,拡散していく方程式である熱拡散方程式の有限要素法解析の方法について述べる.まず熱拡散方程式の定式化を行い,弱形式に変換した後に,有限要素法の離散化を行う.軸対称問題における弱形式化と有限要素法離散化についても触れる.
フーリエの法則より,熱流速ベクトル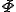 は次のように温度場
は次のように温度場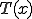 の勾配によって表される.
の勾配によって表される.
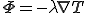 (1)
(1)
但し,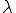 は熱伝導係数であり,温度勾配と熱流速を対応づける正定値対称テンソルである.
は熱伝導係数であり,温度勾配と熱流速を対応づける正定値対称テンソルである.
一方熱量保存の法則により,
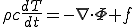 (2)
(2)
が成り立つ.但し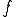 は単位体積あたりの発熱量である.
は単位体積あたりの発熱量である.
(1)の両辺の発散をとり式(2)を代入する.
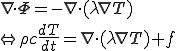
となり,熱拡散方程式が得られる.
| 熱拡散方程式 |
|---|
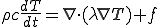 |
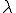 はテンソル量であるが,等方的な物性の場合は温度勾配と熱流速ベクトルの方向が一致するために,スカラー量として扱うことができる.また熱伝導率が一定であることを仮定すると次のようになる.
はテンソル量であるが,等方的な物性の場合は温度勾配と熱流速ベクトルの方向が一致するために,スカラー量として扱うことができる.また熱伝導率が一定であることを仮定すると次のようになる.
| 熱拡散方程式(熱伝導率が等方で一定) |
|---|
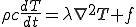 (3) (3) |
式(3)のように熱伝導係数が等方で一定であるとして,式展開を行う.
境界条件としては,次の2つを考える.
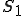 上で
上で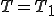 が与えられる
が与えられる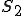 上で単位面積あたりの熱流入量
上で単位面積あたりの熱流入量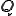 が与えられる.
が与えられる.式(1)のフーリエの法則から
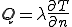
となる.流出量ではなく流入量を境界条件として与えているのは,実際の問題では冷却よりも加熱する場合が多いという現実に即しているものである.
(3)の両辺に固定境界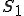 上で0になる任意の仮想変分
上で0になる任意の仮想変分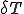 を掛けて解析領域
を掛けて解析領域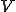 全体で積分し,Gaussの発散定理を適応すると以下のようになる.
全体で積分し,Gaussの発散定理を適応すると以下のようになる.
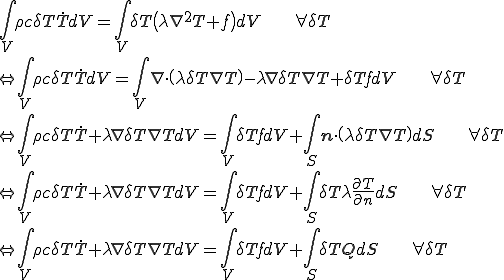
| 弱形式の熱伝導方程式 |
|---|
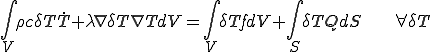 (4) (4) |
領域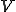 がメッシュ分割されているとしよう.式(4)の積分は各要素内での積分を全て足し合わせて得ることができる.つまり,
がメッシュ分割されているとしよう.式(4)の積分は各要素内での積分を全て足し合わせて得ることができる.つまり,
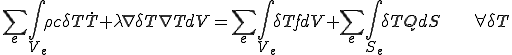 (5)
(5)
ここで,ガラーキン法で変分を行うとして,要素内で次のように補間関数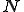 を用いて
を用いて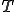 と
と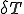 が離散化されているとする.
が離散化されているとする.
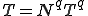 ,
,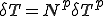
また,領域の表面は次のように補間関数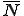 を用いて離散化されているとする.
を用いて離散化されているとする.
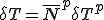
これらを式(5)に代入すると以下のように,要素剛性行列,全体剛性行列を導出することができる.但し,式変形では要素内での番号付け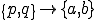 が成り立つとした.
が成り立つとした.
![\sum_e\int_{V_e} \rho c N^p\delta T^pN^q\dot{T}^q + \lambda\nabla N^p\delta T^p\nabla N^qT^qdV= \sum_e\int_{V_e} N^p\delta T^p f dV + \sum_e\int_{S_e} \bar{N}^p\delta T^p Q dS\;\;\;\;\forall\delta T\\ \Leftright \sum_e\(\delta T^p\int_{V_e} \rho c N^pN^q dV \dot{T}^q\) + \sum_e\(\delta T^p\int_{V_e}\lambda\nabla N^p\nabla N^qdVT^q\)= \sum_e\(\delta T^p\int_{V_e} N^p f dV\) + \sum_e\(\delta T^p \int_{S_e} \bar{N}^pQ dS\)\;\;\;\;\forall\delta T\\ \Leftright\delta T^a\(\sum_e M^{pq} \)\dot{T}^b + \delta T^a\(\sum_eA^{pq}\)T^b= \delta T^a\(\sum_e {F_{in}}^p_e \) + \delta T^a\(\sum_e {F_{out}}^p_e \)\;\;\;\;\forall\delta T\\ \Leftright\delta T^a M^{ab} \dot{T}^b + \delta T^a A^{ab}T^b= \delta T^a F_{in}^a + \delta T^a F_{out}^a \;\;\;\;\forall\delta T\\ \Leftright M^{ab} \dot{T}^b + A^{ab}T^b= F_{in}^a + F_{out}^a\\ \Leftright \[M\] \{\dot{T}\} + \[A\]\{T\}= \{F_{in}\} + \{F_{out}\} \sum_e\int_{V_e} \rho c N^p\delta T^pN^q\dot{T}^q + \lambda\nabla N^p\delta T^p\nabla N^qT^qdV= \sum_e\int_{V_e} N^p\delta T^p f dV + \sum_e\int_{S_e} \bar{N}^p\delta T^p Q dS\;\;\;\;\forall\delta T\\ \Leftright \sum_e\(\delta T^p\int_{V_e} \rho c N^pN^q dV \dot{T}^q\) + \sum_e\(\delta T^p\int_{V_e}\lambda\nabla N^p\nabla N^qdVT^q\)= \sum_e\(\delta T^p\int_{V_e} N^p f dV\) + \sum_e\(\delta T^p \int_{S_e} \bar{N}^pQ dS\)\;\;\;\;\forall\delta T\\ \Leftright\delta T^a\(\sum_e M^{pq} \)\dot{T}^b + \delta T^a\(\sum_eA^{pq}\)T^b= \delta T^a\(\sum_e {F_{in}}^p_e \) + \delta T^a\(\sum_e {F_{out}}^p_e \)\;\;\;\;\forall\delta T\\ \Leftright\delta T^a M^{ab} \dot{T}^b + \delta T^a A^{ab}T^b= \delta T^a F_{in}^a + \delta T^a F_{out}^a \;\;\;\;\forall\delta T\\ \Leftright M^{ab} \dot{T}^b + A^{ab}T^b= F_{in}^a + F_{out}^a\\ \Leftright \[M\] \{\dot{T}\} + \[A\]\{T\}= \{F_{in}\} + \{F_{out}\}](46454D20666F72204865617420446966667573696F6E_eq0031.gif)
ここで,![\[M\] \[M\]](46454D20666F72204865617420446966667573696F6E_eq0032.gif) ,
,![\[A\] \[A\]](46454D20666F72204865617420446966667573696F6E_eq0033.gif) ,
,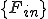
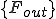 はそれぞれ全体質量行列,全体剛性行列,(体積力からくる)全体外力ベクトル,(表面力からくる)全体外力ベクトルである.
はそれぞれ全体質量行列,全体剛性行列,(体積力からくる)全体外力ベクトル,(表面力からくる)全体外力ベクトルである.
![\[M\]=M^{ab}=\sum_e M^{ab}_e \[M\]=M^{ab}=\sum_e M^{ab}_e](46454D20666F72204865617420446966667573696F6E_eq0036.gif) ,
,![\[A\]=A^{ab}=\sum_e A^{ab}_e \[A\]=A^{ab}=\sum_e A^{ab}_e](46454D20666F72204865617420446966667573696F6E_eq0037.gif) ,
,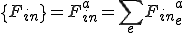 ,
,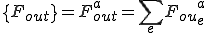
これらは要素単位での次のような行列の足し合わせで得られることが分かる.
| 要素質量行列,剛性行列,外力ベクトル |
|---|
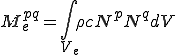 |
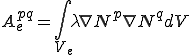 |
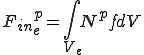 |
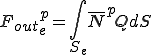 |
得られた温度とその時間微分に関する連立一次方程式を陰的・陽的時間積分スキームを用いて解くことで,時間発展解が得られる.
以下の図のように軸対称な3次元問題について考える,つまり,形状,初期条件,境界条件,物性値全てが軸対称な場合であり,解も軸対称となる.この場合は断面における2次元的な問題に帰着でき,3次元解析のコストを大幅に削減することができる.
軸対称な場合について,断面について2次元的に式(4)を離散化する.熱拡散方程式の弱形式は以下の通りであった.
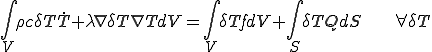
積分の変数を以下のように,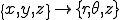 に変換しよう.
に変換しよう.
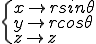
この場合のヤコビアンの絶対値は
![\det J(r,\theta,z)=\det \[\begin{array} \sin\theta & r \cos\theta & 0 \\ \cos\theta & -r\sin\theta & 0 \\ 0 & 0 & 1 \end{array}\] = r \det J(r,\theta,z)=\det \[\begin{array} \sin\theta & r \cos\theta & 0 \\ \cos\theta & -r\sin\theta & 0 \\ 0 & 0 & 1 \end{array}\] = r](46454D20666F72204865617420446966667573696F6E_eq0047.gif)
となるので,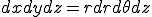 となる.また,この場合下の図のように,
となる.また,この場合下の図のように,
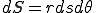
が成り立つので,これを上に代入すると,
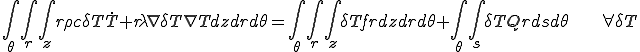
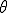 方向に被積分関数は変化しないので,
方向に被積分関数は変化しないので,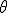 の積分を取り除くことができる.また,断面の2次元的な積分領域を
の積分を取り除くことができる.また,断面の2次元的な積分領域を ,断面の境界を
,断面の境界を のように書くと,下のような軸対称問題についての弱形式化が得られる.
のように書くと,下のような軸対称問題についての弱形式化が得られる.
| 軸対称問題についての熱拡散方程式の弱形式 |
|---|
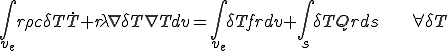 (5) (5) |
領域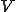 がメッシュ分割されているとしよう.式(4)の積分は各要素内での積分を全て足し合わせて得ることができる.つまり,
がメッシュ分割されているとしよう.式(4)の積分は各要素内での積分を全て足し合わせて得ることができる.つまり,
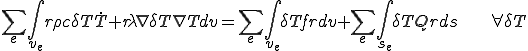 (5)
(5)
ここで,ガラーキン法で変分を行うとして,要素内で次のように補間関数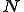 を用いて
を用いて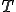 と
と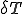 が離散化されているとする.
が離散化されているとする.
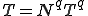 ,
,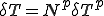
また,領域の表面は次のように補間関数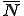 を用いて離散化されているとする.
を用いて離散化されているとする.
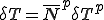
これらを式(5)に代入すると以下のように,要素剛性行列,全体剛性行列を導出することができる.但し,式変形では要素内での番号付け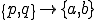 が成り立つとした.
が成り立つとした.
![\sum_e\int_{v_e} r\rho c N^p\delta T^pN^q\dot{T}^q + r\lambda\nabla N^p\delta T^p\nabla N^qT^qdv= \sum_e\int_{v_e} rN^p\delta T^p f dv + \sum_e\int_{s_e} r\bar{N}^p\delta T^p Q ds\;\;\;\;\forall\delta T\\ \Leftright \sum_e\(\delta T^p\int_{v_e} r\rho c N^pN^q dV \dot{T}^q dv\) + \sum_e\(\delta T^p\int_{v_e}r\lambda\nabla N^p\nabla N^qdVT^q dv\)\\\;\;\;\;\;\;\;\;= \sum_e\(\delta T^p\int_{v_e}r N^p f dv\) + \sum_e\(\delta T^p \int_{s_e}r \bar{N}^pQ dS\)\;\;\;\;\forall\delta T\\ \Leftright\delta T^a\(\sum_e M^{pq} \)\dot{T}^b + \delta T^a\(\sum_eA^{pq}\)T^b= \delta T^a\(\sum_e {F_{in}}^p_e \) + \delta T^a\(\sum_e {F_{out}}^p_e \)\;\;\;\;\forall\delta T\\ \Leftright\delta T^a M^{ab} \dot{T}^b + \delta T^a A^{ab}T^b= \delta T^a F_{in}^a + \delta T^a F_{out}^a \;\;\;\;\forall\delta T\\ \Leftright M^{ab} \dot{T}^b + A^{ab}T^b= F_{in}^a + F_{out}^a\\ \Leftright \[M\] \{\dot{T}\} + \[A\]\{T\}= \{F_{in}\} + \{F_{out}\} \sum_e\int_{v_e} r\rho c N^p\delta T^pN^q\dot{T}^q + r\lambda\nabla N^p\delta T^p\nabla N^qT^qdv= \sum_e\int_{v_e} rN^p\delta T^p f dv + \sum_e\int_{s_e} r\bar{N}^p\delta T^p Q ds\;\;\;\;\forall\delta T\\ \Leftright \sum_e\(\delta T^p\int_{v_e} r\rho c N^pN^q dV \dot{T}^q dv\) + \sum_e\(\delta T^p\int_{v_e}r\lambda\nabla N^p\nabla N^qdVT^q dv\)\\\;\;\;\;\;\;\;\;= \sum_e\(\delta T^p\int_{v_e}r N^p f dv\) + \sum_e\(\delta T^p \int_{s_e}r \bar{N}^pQ dS\)\;\;\;\;\forall\delta T\\ \Leftright\delta T^a\(\sum_e M^{pq} \)\dot{T}^b + \delta T^a\(\sum_eA^{pq}\)T^b= \delta T^a\(\sum_e {F_{in}}^p_e \) + \delta T^a\(\sum_e {F_{out}}^p_e \)\;\;\;\;\forall\delta T\\ \Leftright\delta T^a M^{ab} \dot{T}^b + \delta T^a A^{ab}T^b= \delta T^a F_{in}^a + \delta T^a F_{out}^a \;\;\;\;\forall\delta T\\ \Leftright M^{ab} \dot{T}^b + A^{ab}T^b= F_{in}^a + F_{out}^a\\ \Leftright \[M\] \{\dot{T}\} + \[A\]\{T\}= \{F_{in}\} + \{F_{out}\}](46454D20666F72204865617420446966667573696F6E_eq0066.gif)
ここで,![\[M\] \[M\]](46454D20666F72204865617420446966667573696F6E_eq0067.gif) ,
,![\[A\] \[A\]](46454D20666F72204865617420446966667573696F6E_eq0068.gif) ,
,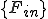
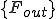 はそれぞれ全体質量行列,全体剛性行列,(体積力からくる)全体外力ベクトル,(表面力からくる)全体外力ベクトルである.
はそれぞれ全体質量行列,全体剛性行列,(体積力からくる)全体外力ベクトル,(表面力からくる)全体外力ベクトルである.
![\[M\]=M^{ab}=\sum_e M^{ab}_e \[M\]=M^{ab}=\sum_e M^{ab}_e](46454D20666F72204865617420446966667573696F6E_eq0071.gif) ,
,![\[A\]=A^{ab}=\sum_e A^{ab}_e \[A\]=A^{ab}=\sum_e A^{ab}_e](46454D20666F72204865617420446966667573696F6E_eq0072.gif) ,
,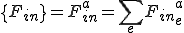 ,
,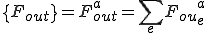
これらは要素単位での次のような行列の足し合わせで得られることが分かる.
| 要素質量行列,剛性行列,外力ベクトル |
|---|
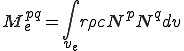 |
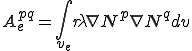 |
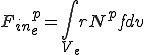 |
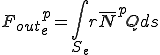 |
三角形一次要素を用いて補間を行った場合,解析的に剛性行列を導出することができる.このような一次要素による線形な補間関数を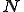 の変わりに
の変わりに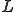 を使って表す.
を使って表す.
軸までの距離 も三角形内で一次的に変化するから
も三角形内で一次的に変化するから
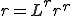
というように,節点の値の補間によって得ることができる.これを用いて計算してみよう.
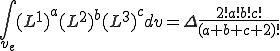 (6);
(6);
が成り立つことを利用する.但し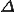 は三角形の面積であるとする.
は三角形の面積であるとする.
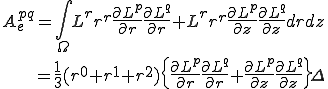
結局この場合,重心位置での距離に2次元三角形のラプラス方程式の要素剛性を掛けたものになることが分かる.
要素質量行列を計算する.式(6)から以下が成り立つ
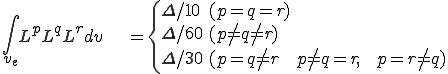
これて次の要素質量行列は
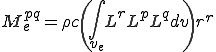
は次のように書ける.
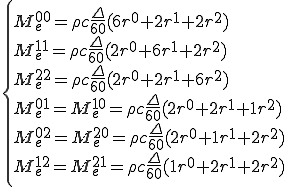
「有限要素法による構造解析事例集」という本に載っている,円盤を周囲から冷やすした時の温度分布の時間履歴を調べるという例題を解いてみた.これを解くことでプログラムの精度検証を行った.問題の概要は,次のとおりである.
半径が1mで厚さが0.1mの円盤を初期状態t=0では全体が500℃として,t>0で円周を0℃として境界条件を設定する.円盤の物性値は鉄として,
熱伝導率(α):48.0 W/(mK) 比熱(c) : 480 J/(kg℃) 密度(ρ) : 7.86*10^3 kg/m^3
のように設定する.このような熱拡散問題における,温度の時間履歴は厳密解が次のようになっている.
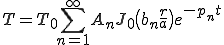
ただし,a:円盤の半径,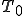 :初期温度,
:初期温度,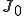 :0次のベッセル関数,:0次のベッセル関数の根,
:0次のベッセル関数,:0次のベッセル関数の根,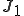 :1次のベッセル関数,
:1次のベッセル関数,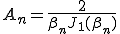 ,
,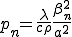
さて,これを有限要素法で解析を行う.軸対称性を用いて下のように断面の2次元的な領域でのみ解析を行った.
補間関数は三角形1次要素として,時間積分は時間刻み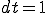 として,Crank-Nicolson法を用いた.ある時刻における断面の有限要素法解は次のとおり.
として,Crank-Nicolson法を用いた.ある時刻における断面の有限要素法解は次のとおり.
2時間後の温度分布の厳密解と有限要素法解の比較は次のとおり
有限要素法解が厳密解にぴったり合っていることが分かる
| 有限要素法概説―理工学における基礎と応用 (FEM+BEM (3)) |
菊池文雄 著 |
| 流れと熱伝導の有限要素法入門 | 矢川元基 著 |
| 有限要素法による構造解析事例集 基礎問題から実務レベル問題まで | 白鳥正樹,三好俊朗著 |