Stress Rate

応力速度

Last Update:2009年05月06日

概要

物質の歪みと応力の関係を表す構成式を作るためには、構成式が物質客観性を満足する必要がある．つまり、もし歪みが客観性を持つ場合は応力も客観性を持つ必要がある．物質の変形と関係のない、観測者の回転や移動によって応力が発生してしまう矛盾を避けるためである．

弾塑性体などは速度型の構成式で記述されるのが一般的である．つまり弾塑性体は歪速度と応力速度を結びつける式によって表現される．この時歪みとしては、客観性をもつ歪速度テンソルを用いる．よって応力速度も客観性を持たせなければならない．Cauchy応力を直接時間微分したテンソルには客観性がなく、歪速度と関連付けることはできない．Cauchy応力や相対Kirchohoff応力の客観性を持つような速度を取ったものを用いる．このような速度の取り方は

Jauman速度
Oldroyd速度
Cotter-Rivelin速度
Green-Naghdi速度

などが挙げられる．以下それぞれについて詳しく説明する．

Cauchy応力の各種速度

Cauchy応力テンソル $\b{T}$ はある共変や反変基底ベクトルによって次のように成分表示される．

$\b{T} = T^{ij}\b{g}_i\otimes\b{g}_j = T_{ij}\b{g}^i\otimes\b{g}^j$

$\dot{\b{T}} = \dot{T}^{ij}\b{g}_i\otimes\b{g}_j + T^{ij}\dot{\b{g}}_i\otimes\b{g}_j + T^{ij}\b{g}_i\otimes\dot{\b{g}}_j\\\;\;\; = \dot{T}_{ij}\b{g}^i\otimes\b{g}^j + T_{ij}\dot{\b{g}}^i\otimes\b{g}^j + T_{ij}\b{g}^i\otimes\dot{\b{g}}^j$

基底ベクトルの時間変化を取り除いた応力の速度は次のようになる．

共変基底ベクトルの変化を考えた場合は

$\dot{T}^{ij}\b{g}_i\otimes\b{g}_j = \dot{\b{T}} - T^{ij}\dot{\b{g}}_i\otimes\b{g}_j - T^{ij}\b{g}_i\otimes\dot{\b{g}}_j$

反変基底ベクトルの変化を考えた場合は

$\dot{T}_{ij}\b{g}^i\otimes\b{g}^j = \dot{\b{T}} - T_{ij}\dot{\b{g}}^i\otimes\b{g}^j - T_{ij}\b{g}^i\otimes\dot{\b{g}}^j$

基底ベクトルを時間変化させるやり方によって、Jauman速度 $\dot{\b{T}}^{(J)}$ 、Oldroyd速度 $\dot{\b{T}}^{(O)}$ 、Cotter-Rivelin速度 $\dot{\b{T}}^{(C)}$ などの時間微分の種類がある．

Cauchy応力のJauman速度

応力の変化から現時刻の回転の分を差し引いたものをJauman速度という．

共変基底ベクトルの時間変化が物質の回転に従うとして、回転速度テンソル $\b{W}$ を用いて

$\dot{\b{g}}_i = \b{W}\cdot \b{g}_i$

としたときの、基底ベクトルの変化分を取り除いた応力の速度を計算する．

$\dot{\b{T}}^{(J)} = \dot{T}^{ij}\b{g}_i\otimes\b{g}_j = \dot{\b{T}} - T^{ij}\dot{\b{g}}_i\otimes\b{g}_j - T^{ij}\b{g}_i\otimes\dot{\b{g}}_j\\\;\;\;\;\; = \dot{\b{T}} - T^{ij}(\b{W}\cdot\b{g}_i)\otimes\b{g}_j - T^{ij}\b{g}_i\otimes(\b{W}\cdot\b{g}_j)\\\;\;\;\;\; = \dot{\b{T}} - \b{W}\cdot(T^{ij}\b{g}_i\otimes\b{g}_j) - (T^{ij}\b{g}_i\otimes\b{g}_j)\cdot\b{W}^T\\\;\;\;\;\; = \dot{\b{T}} - \b{W}\cdot\b{T} - \b{T}\cdot\b{W}^T\\\;\;\;\;\; = \dot{\b{T}} - \b{W}\cdot\b{T} + \b{T}\cdot\b{W}$

Cauchy応力のJauman速度
$\dot{\b{T}}^{(J)} = \dot{\b{T}} - \b{W}\cdot\b{T} + \b{T}\cdot\b{W}$

Cauchy応力のGreen-Naghdi速度

応力の変化から基準時刻からの剛体回転の分を差し引いたものをGreen-Naghdi速度という．

共変基底ベクトルが基準時刻 t_0=0 からの物質の剛体回転 $\b{R}$ に従うとして、

$\b{g}_i(t) = \b{R}\cdot\b{g}_i(0)$

$\dot{\b{g}}_i(t) = \dot{\b{R}}\cdot\b{g}_i(0) = \dot{\b{R}}\cdot\b{R}^{-1}\b{g}_i(t) = \dot{\b{R}}\cdot\b{R}^T\b{g}_i(t)$

となる． $\b{\Omega} = \dot{\b{R}}\cdot\b{R}^T$ とおくと、

$\dot{\b{g}}_i = \b{\Omega}\cdot \b{g}_i$

となる．この時の基底ベクトルの変化分を取り除いた応力の速度を計算する．

$\dot{\b{T}}^{(G)} = \dot{T}^{ij}\b{g}_i\otimes\b{g}_j = \dot{\b{T}} - T^{ij}\dot{\b{g}}_i\otimes\b{g}_j - T^{ij}\b{g}_i\otimes\dot{\b{g}}_j\\\;\;\;\;\; = \dot{\b{T}} - T^{ij}(\b{\Omega}\cdot\b{g}_i)\otimes\b{g}_j - T^{ij}\b{g}_i\otimes(\b{\Omega}\cdot\b{g}_j)\\\;\;\;\;\; = \dot{\b{T}} - \b{\Omega}\cdot(T^{ij}\b{g}_i\otimes\b{g}_j) - (T^{ij}\b{g}_i\otimes\b{g}_j)\cdot\b{\Omega}^T\\\;\;\;\;\; = \dot{\b{T}} - \b{\Omega}\cdot\b{T} - \b{T}\cdot\b{\Omega}^T\\\;\;\;\;\; = \dot{\b{T}} - \b{\Omega}\cdot\b{T} + \b{T}\cdot\b{\Omega}$

Cauchy応力のGreen-Naghdi速度
$\dot{\b{T}}^{(G)} = \dot{\b{T}} - \b{\Omega}\cdot\b{T} + \b{T}\cdot\b{\Omega}$

ここで、次で示される $\Omega$ の反対称性を利用した．

$\b{\Omega}^T = (\dot{\b{R}}\cdot\b{R}^T)^T = \b{R}\cdot\dot{\b{R}}^T = \dot{\b{R}}\cdot\b{R}^T + \b{R}\cdot\dot{\b{R}}^T - \dot{\b{R}}\cdot\b{R}^T\\\;\;\;\; = (\b{R}\cdot\b{R}^T)^.- \dot{\b{R}}\cdot\b{R}^T\\\;\;\;\; = I^.- \dot{\b{R}}\cdot\b{R}^T\\\;\;\;\; = - \dot{\b{R}}\cdot\b{R}^T\\\;\;\;\; = -\Omega$

Cauchy応力のOldroyd速度

応力の変化から速度勾配による共変基底ベクトルの変化を差し引いた時の、反変成分の変化による速度をOldroyd速度という．

共変基底ベクトルの時間変化が物質とともに変形するとして、

$\dot{\b{g}}_i = \b{L}\cdot \b{g}_i$

としたときの、基底ベクトルの変化分を取り除いた応力の速度を計算する．

$\dot{\b{T}}^{(O)} = \dot{T}^{ij}\b{g}_i\otimes\b{g}_j = \dot{\b{T}} - T^{ij}\dot{\b{g}}_i\otimes\b{g}_j - T^{ij}\b{g}_i\otimes\dot{\b{g}}_j\\\;\;\;\;\; = \dot{\b{T}} - T^{ij}(\b{L}\cdot\b{g}_i)\otimes\b{g}_j - T^{ij}\b{g}_i\otimes(\b{L}\cdot\b{g}_j)\\\;\;\;\;\; = \dot{\b{T}} - \b{L}\cdot(T^{ij}\b{g}_i\otimes\b{g}_j) - (T^{ij}\b{g}_i\otimes\b{g}_j)\cdot\b{L}^T\\\;\;\;\;\; = \dot{\b{T}} - \b{L}\cdot\b{T} - \b{T}\cdot\b{L}^T$

Cauchy応力のOldroyd速度
$\dot{\b{T}}^{(O)} = \dot{\b{T}} - \b{L}\cdot\b{T} - \b{T}\cdot\b{L}^T$

Jauman速度とOldroyd速度の間には

$\dot{\b{T}}^{(J)} = \dot{\b{T}} - \b{W}\cdot\b{T} - \b{T}\cdot\b{W}^T\\\;\;\;\;\; = \dot{\b{T}} - (\b{L}-\b{D})\cdot\b{T} - \b{T}\cdot(\b{L}-\b{D})^T\\\;\;\;\;\; = \dot{\b{T}} - \b{L}\cdot\b{T}+\b{D}\cdot\b{T} - \b{T}\cdot\b{L}^T+\b{T}\cdot\b{D}^T\\\;\;\;\;\; = \dot{\b{T}}^{(O)}+\b{D}\cdot\b{T}+\b{T}\cdot\b{D}$

の関係がある．

Cauchy応力のCotter-Rivelin速度

応力の変化から速度勾配による共変基底ベクトルの変化を差し引いた時の、共変成分の変化による速度をCotter-Rivelin速度という．

共変基底ベクトルの時間変化が物質とともに変形するとして、

$\dot{\b{g}}_i = \b{L}\cdot \b{g}_i$

このよき、反変基底ベクトルの変化を求めてみよう．

$\frac{d}{dt}(\b{g}^i\cdot\b{g}_j) = \frac{d}{dt}(\delta^i_j) = 0\\\;\;\;\;\; = \dot{\b{g}}^i\cdot\b{g}_j + \b{g}^i\cdot\dot{\b{g}}_j\\\;\;\;\;\; = \dot{\b{g}}^i\cdot\b{g}_j + \b{g}^i\cdot(\b{L}\cdot\b{g}_j)\\\;\;\;\;\; = \dot{\b{g}}^i\cdot\b{g}_j + (\b{L}^T\cdot\b{g}^i)\cdot\b{g}_j\\\Leftright\dot{\b{g}}^i\cdot\b{g}_j = (-\b{L}^T\cdot\b{g}^i)\cdot\b{g}_j\\\Leftright\dot{\b{g}}^i = -\b{L}^T\cdot \b{g}^i$

これらを代入すると、

$\dot{\b{T}}^{(C)} = \dot{T}_{ij}\b{g}^i\otimes\b{g}^j = \dot{\b{T}} - T_{ij}\dot{\b{g}}^i\otimes\b{g}^j - T_{ij}\b{g}^i\otimes\dot{\b{g}}^j\\\;\;\;\;\; = \dot{\b{T}} - T_{ij}(-\b{L}^T\cdot\b{g}^i)\otimes\b{g}^j - T_{ij}\b{g}^i\otimes(-\b{L}^T\cdot\b{g}^j)\\\;\;\;\;\; = \dot{\b{T}} + \b{L}^T\cdot(T_{ij}\b{g}^i\otimes\b{g}^j) + (T_{ij}\b{g}^i\otimes\b{g}^j)\cdot\b{L}\\\;\;\;\;\; = \dot{\b{T}} + \b{L}^T\cdot\b{T} + \b{T}\cdot\b{L}$

Cauchy応力のCotter-Rivelin速度
$\dot{\b{T}}^{(C)} = = \dot{\b{T}} + \b{L}^T\cdot\b{T} + \b{T}\cdot\b{L}$

各種応力速度の関係

$\b{L} = \b{W} + \b{D}$

であり、 $\b{D}=0$ つまり、変形が変化しないときは

$\dot{\b{T}}^{(J)} = \dot{\b{T}}^{(O)} = \dot{\b{T}}^{(C)}$

である．

相対Kirchhoff応力の速度

J_t はの時間を基準とした微小領域の体積変化率である．における基準を計算しているので

J_t(t)=1

である．歪速度テンソルとすると、

$\dot{J}_t = \tr\b{D}$

が成り立つ．

の時間を基準とした相対kirchhoff応力 $\hat{\b{T}}$ は次のように表される．

相対kirchhoff応力
$\hat{\b{T}} = J_t\b{T}$

$\dot{\hat{\b{T}}} = \dot{J}_t\b{T} + J_t\dot{\b{T}} = \b{T}\tr\b{D} + \dot{\b{T}}$

相対Kirchhoff応力のJauman速度

$\dot{\hat{\b{T}}}^{(J)} = \dot{\hat{\b{T}}} - \b{W}\cdot\hat{\b{T}} - \hat{\b{T}}\cdot\b{W}^T = \b{T}\tr\b{D} + \dot{\b{T}} - \b{W}\cdot\b{T} - \b{T}\cdot\b{W}^T\\\;\;\;\;\; = \dot{\b{T}}^{(J)} + \b{T}\tr\b{D}$

相対Kirchhoff応力のOldroyd速度

$\dot{\hat{\b{T}}}^{(O)} = \dot{\hat{\b{T}}} - \b{L}\cdot\hat{\b{T}} - \hat{\b{T}}\cdot\b{L}^T = \b{T}\tr\b{D} + \dot{\b{T}} - \b{L}\cdot\b{T} - \b{T}\cdot\b{L}^T\\\;\;\;\;\; = \dot{\b{T}}^{(O)} + \b{T}\tr\b{D}$

相対Kirchhoff応力のCotter-Rivelin速度

$\dot{\hat{\b{T}}}^{(C)} = \dot{\hat{\b{T}}} + \b{L}^T\cdot\hat{\b{T}} + \hat{\b{T}}\cdot\b{L} = \b{T}\tr\b{D} + \dot{\b{T}} + \b{L}^T\cdot\b{T} + \b{T}\cdot\b{L}\\\;\;\;\;\; = \dot{\b{T}}^{(C)} + \b{T}\tr\b{D}$

相対Kirchhoff応力のGreen-Nargdi速度

$\dot{\hat{\b{T}}}^{(G)} = \dot{\hat{\b{T}}} - \b{\Omega}\cdot\hat{\b{T}} - \hat{\b{T}}\cdot\b{\Omega}^T = \b{T}\tr\b{D} + \dot{\b{T}} - \b{\Omega}\cdot\b{T} - \b{T}\cdot\b{\Omega}^T\\\;\;\;\;\; = \dot{\b{T}}^{(G)} + \b{T}\tr\b{D}$

Truesdellの応力速度

時刻ｔを基準配置とした第二Piola-Kirchhoff応力の速度をTruesdell応力速度と呼ぶ．

時刻を基準とした相対変形勾配テンソル $\b{F}_t$ を考える

$\b{F}_t(t) = I$

$\dot{\b{F}}_t = \b{L}$

が成り立つ．この時、時刻を基準にした、第二Piola-Kirchhoff応力 $\b{S}_t$ は次のように定義される．

$\b{F}_t\cdot\b{S}_t\cdot\b{F}_t^T = J_t\b{T}$

であることがわかる．

$\b{S}_t(t) = \b{T}$

2個上の式を両辺微分して比較してみよう．

左辺は
$(\b{F}_t\cdot\b{S}_t\cdot\b{F}_t^T)^{.} = \dot{\b{F}}_t\cdot\b{S}_t\cdot\b{F}_t^T + \b{F}_t\cdot\dot{\b{S}}_t\cdot\b{F}_t^T + \b{F}_t\cdot\b{S}_t\cdot\dot{\b{F}}_t^T\\\;\;\;\;\; = \b{L}\cdot\b{T} + \dot{\b{S}}_t + \b{T}\cdot\b{L}^T$

右辺は
$(J_t\b{T})^{.} = \dot{J}_t\b{T}+J_t\dot{\b{T}}\\\;\;\;\;\; = \b{T}\tr\b{D} + \dot{\b{T}}$

よって両辺を比較すると次のようになる．

$\dot{\b{S}}_t = \dot{\b{T}} - \b{L}\cdot\b{T} - \b{T}\cdot\b{L}^T + \b{T}\tr\b{D}\\\;\;\;\; = \dot{\b{T}}^{(O)}+\b{T}\tr\b{D}\\\;\;\;\; = \dot{\hat{\b{T}}}^{(O)}$

Truesdell応力速度は相対Kirchhoff応力のOldroyd速度と等しいことがわかる．

Truesdell応力速度とJauman速度は次のような関係がある．

$\dot{\b{S}}_t = \dot{\b{T}}^{(O)}+\b{T}\tr\b{D}\\\;\;\;\; = \dot{\b{T}}^{(J)}-\b{D}\cdot\b{T}-\b{T}\cdot\b{D} + \b{T}\tr\b{D}$

まとめ

相対Kirchhoff応力とCauchy応力の各速度について次が成り立つことがわかる．

相対Kirchohoff応力とCauch応力の各種速度の関係
$\{\begin{array}{l}\dot{\hat{\b{T}}}^{(J)} = \dot{\b{T}}^{(J)} + \b{T}\tr\b{D}\\ \dot{\hat{\b{T}}}^{(O)} = \dot{\b{T}}^{(O)} + \b{T}\tr\b{D} = \dot{\b{S}}_t \\ \dot{\hat{\b{T}}}^{(G)} = \dot{\b{T}}^{(G)} + \b{T}\tr\b{D}\\ \dot{\hat{\b{T}}}^{(C)} = \dot{\b{T}}^{(C)} + \b{T}\tr\b{D}\end{array}$

応力速度の客観性

歪速度テンソルから応力速度テンソルを求める構成式を作る場合を考えよう．歪み速度テンソルには客観性があるので、応力速度テンソルにも客観性がなければならない．客観性がなければ、例えばある物体を違った角度から見ただけで応力が発生してしまうという矛盾を持ってしまう．

物体を異なる角度から見たときにテンソルがどのような変換を受けるのかということを調べるために、ある観測者から見た位置 $\b{x}$ が別の観測者から見ると $\b{x}^*$ の位置にあり、両者の関係が次のように表される場合を考えよう．

$\b{x}^* = \b{c}(t) + \b{Q}(t)\cdot\b{x}$

これを図で表すと次のようになる．

2人の観測者から見たPの位置の関係

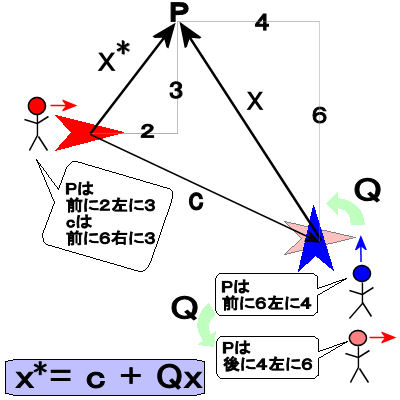各観測者から見たベクトルを(前,左)のように表す．画面右を向いている赤い人から見るとPの位置は $\b{x}^=(2,3)$ に、ベクトル $\b{c}$ はに見える．画面上を向いている青い人からみるとPの位置は $\b{x}=(6,4)$ に見える．青い人の向きは赤い人の向きを反時計回りに９０度回転したものである． $\b{Q}$ =９０度回転青い人の位置において赤い人の向きから見たPの位置は $\b{Q}\cdot\b{x}=(-4,6)$ である．結局赤い人から見たPの位置は $\b{x}^=\b{c}+\b{Q}\cdot\b{x}=(6,-3)+(-4,6)=(2,3)$ となる．

2人の観測者から見たPの位置の関係

各観測者から見たベクトルを(前,左)のように表す．
画面右を向いている赤い人から見るとPの位置は $\b{x}^*=(2,3)$ に、ベクトル $\b{c}$ は (6,-3)

に見える．
画面上を向いている青い人からみるとPの位置は $\b{x}=(6,4)$ に見える．
青い人の向きは赤い人の向きを反時計回りに９０度回転したものである． $\b{Q}$ =９０度回転
青い人の位置において赤い人の向きから見たPの位置は $\b{Q}\cdot\b{x}=(-4,6)$ である．
結局赤い人から見たPの位置は $\b{x}^*=\b{c}+\b{Q}\cdot\b{x}=(6,-3)+(-4,6)=(2,3)$ となる．

さて、このような関係がある場合に相対的な位置を表すベクトルの変換を考えよう．

$\b{x}_2^* - \b{x}_1^* = $\b{c}(t) + \b{Q}(t)\cdot\b{x}_2$ - $\b{c}(t) + \b{Q}(t)\cdot\b{x}_1$\\\;\;\; = \b{Q}(t)$\b{x}_2-\b{x}_1$$

が成り立つ．よって相対的な位置を表すベクトル $\b{b}$ が客観性を持つとき

$\b{b}^* = \b{Q}\cdot\b{b}$

が成り立たなければならないことがわかる．

ベクトル $\b{b}$ がテンソル $\b{K}$ によってベクトル $\b{c}$ に変換されるとしよう．

$\b{c}^* = \b{K}^*\cdot\b{b}^*\;\Leftright\; \b{Q}\cdot\b{c}=\b{K}^*\cdot\b{Q}\cdot\b{b} \;\Leftright\; \b{c} = $\b{Q}^T\cdot\b{K}^*\cdot\b{Q}$\cdot\b{b}$

$\b{K} = \b{Q}^T\cdot\b{K}^*\cdot\b{Q}$

が成り立つ．よって、テンソル $\b{K}$ に客観性があるとすると、

$\b{K}^* = \b{Q}\cdot\b{K}\cdot\b{Q}^T$

のような関係が成り立つ．

ここで気をつけたいのは観測者の移動と基底ベクトルの回転は別の物だということだ．基底ベクトルを回転しても成分は変わるがテンソル自体は変わらない．観測者と観測対象の位置関係は相対的なものであるから、観測者の移動や回転は観測対象の移動や回転と同じ意味を持つ

各種テンソルの客観性

各種テンソルについて客観性があるのかどうか調べてみよう．

Cauchy応力

Cauchy応力は定義から次のように変換されるので、客観性がある．

$\b{T}^* = \b{Q}\cdot\b{T}\b{Q}^T$

変形勾配テンソル

変形勾配テンソル $\b{F}$ について、

$\b{F}^* = \b{Q}\cdot\b{F}$

が成り立つ．

$\b{F}$ を直交テンソル $\b{R}$ と正値対称テンソル $\b{U}$ に右極分解したものを $\b{F} = \b{R}\cdot\b{U}$ 、

同じく、 $\b{F}^*$ を右極分解したものを $\b{F}^*=\b{R}^*\cdot\b{U}^*$ とする．

$\b{F}^* = \b{Q}\cdot\b{F} = \b{Q}\cdot\b{R}\cdot\b{U} = \b{R}^*\cdot\b{U}^*$

となる． $\b{Q}\cdot\b{R}$ もまた直交テンソルであり、極分解が一意であるから

$\b{U}^* = \b{U}$

$\b{R}^* = \b{Q}\cdot\b{R}$

が成り立つ．

速度勾配テンソル

速度勾配テンソル(velocity gradient tensor)は、

$\b{L}^* = \dot{\b{F}}^*{\b{F}^*}^{-1} = (\b{Q}\cdot\b{F})^.\cdot(\b{Q}\cdot\b{F})^{-1}\\\;\;\; = (\dot{\b{Q}}\cdot\b{F}+\b{Q}\cdot\dot{\b{F}})\cdot(\b{F}^{-1}\cdot\b{Q}^{-1})\\\;\;\; = \dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\dot{\b{F}}\cdot\b{F}^{-1}\cdot\b{Q}^T\\\;\;\; = \dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{L}\cdot\b{Q}^T$

ここで、 $(\b{Q}\cdot\b{Q}^T)^{.} = \b{I}^{.} = 0 = \dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\dot{\b{Q}}^T\;\Leftright\; \dot{\b{Q}}\cdot\b{Q}^T = -\b{Q}\cdot\dot{\b{Q}}^T$ の関係を利用した．

歪み速度テンソル

歪み速度テンソル(strain rate tensor)は

$\b{D}^* = \frac{1}{2}(\b{L}^*+{\b{L}^*}^T) = \frac{1}{2}(\dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{L}\cdot\b{Q}^T + \b{Q}\cdot\dot{\b{Q}}^T + \b{Q}\cdot\b{L}^T\cdot\b{Q}^T)\\\;\;\; = \frac{1}{2}(\b{Q}\cdot\b{Q}^T)^{.}+\b{Q}\cdot\frac{1}{2}(\b{L}+\b{L}^T)\cdot\b{Q}^T\\\;\;\; = \b{Q}\cdot\b{D}\cdot\b{Q}^T$

変形速度テンソルには客観性があることがわかる．

回転速度テンソル

回転速度テンソル(rotation rate tensor) $\b{W}$ は

$\b{W}^* = \b{L}^* - \b{D}^*\\\;\;\; = \dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{L}\cdot\b{Q}^T - \b{Q}\cdot\b{D}\cdot\b{Q}^T\\\;\;\; = \dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot(\b{L}-\b{D})\cdot\b{Q}^T\\\;\;\; = \dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{W}\cdot\b{Q}^T$

剛体回転速度テンソル

剛体回転速度テンソル $\b{\Omega}$ は

$\b{\Omega}^* = \dot{\b{R}}^*\cdot{\b{R}^*}^T = (\b{Q}\cdot\b{R})^.\cdot(\b{Q}\cdot\b{R})^T = (\b{Q}\cdot\dot{\b{R}}+\dot{\b{Q}}\cdot\b{R})\cdot\b{R}^T\cdot\b{Q}^T = \dot{\b{Q}}\cdot\b{Q}^T+\b{Q}\cdot\dot{\b{R}}\cdot\b{R}^T\cdot\b{Q}^T\\\;\;\;\; = \dot{\b{Q}}\cdot\b{Q}^T+\b{Q}\cdot\b{\Omega}\cdot\b{Q}^T$

Cauchy応力を時間微分したテンソルに客観性がない

$\dot{\b{T}}^* = \dot{\b{Q}}\cdot\b{T}\b{Q}^T + \b{Q}\cdot\dot{\b{T}}\b{Q}^T + \b{Q}\cdot\b{T}\dot{\b{Q}}^T\\\;\;\;\;\; \ne \b{Q}\cdot\dot{\b{T}}\b{Q}^T$

よって、 $\dot{\b{T}}$ には客観性がない．よって客観性のある歪速度テンソル $\b{D}$ と関連づけて構成式を作ることができないことがわかる．

Cauchy応力の各種速度の客観性

Jauman速度 $\dot{\b{T}}^{(J)}$ 、Oldroyd速度 $\dot{\b{T}}^{(O)}$ 、Green-Nargdi速度 $\dot{\b{T}}^{(G)}$ 、Cotter-Rivelin速度 $\dot{\b{T}}^{(C)}$ はそれぞれ客観性をもつ．実際に計算を行うことでこれを確かめてみよう．

Cauchy応力のJauman速度の客観性

$\b{W}^* = \dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{W}\cdot\b{Q}^T = -\b{Q}\cdot\dot{\b{Q}}^T + \b{Q}\cdot\b{W}\cdot\b{Q}^T$

であることを用いて

$\dot{\b{T}}^{(J)*} = \dot{\b{T}}^* - \b{W}^*\cdot\b{T}^* + \b{T}^*\cdot\b{W}^*\\\;\;\;\;\; = \dot{\b{Q}}\cdot\b{T}\b{Q}^T + \b{Q}\cdot\dot{\b{T}}\b{Q}^T + \b{Q}\cdot\b{T}\dot{\b{Q}}^T\\\;\;\;\;\;\;\; - (\dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{W}\cdot\b{Q}^T)\cdot\b{Q}\cdot\b{T}\cdot\b{Q}^T\\\;\;\;\;\;\;\; + \b{Q}\cdot\b{T}\cdot\b{Q}^T\cdot(-\b{Q}\cdot\dot{\b{Q}}^T + \b{Q}\cdot\b{W}\cdot\b{Q}^T)\\\;\;\;\;\; = \b{Q}\cdot(\dot{\b{T}}-\b{W}\cdot\b{T}+\b{T}\cdot\b{W})\cdot\b{Q}^T\\\;\;\;\;\; = \b{Q}\cdot\dot{\b{T}}^{(J)}\cdot\b{Q}^T$

Cauchy応力のJauman速度には客観性があることがわかる．

Cauchy応力のOldroyd速度の客観性

$\b{L}^* = \dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{L}\cdot\b{Q}^T = -\b{Q}\cdot\dot{\b{Q}}^T + \b{Q}\cdot\b{L}\cdot\b{Q}^T$

であることを用いて

$\dot{\b{T}}^{(O)*} = \dot{\b{T}}^* - \b{L}^*\cdot\b{T}^* - \b{T}^*\cdot{\b{L}^*}^T\\\;\;\;\;\; = \dot{\b{Q}}\cdot\b{T}\b{Q}^T + \b{Q}\cdot\dot{\b{T}}\b{Q}^T + \b{Q}\cdot\b{T}\dot{\b{Q}}^T\\\;\;\;\;\;\;\; - (\dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{L}\cdot\b{Q}^T)\cdot\b{Q}\cdot\b{T}\cdot\b{Q}^T\\\;\;\;\;\;\;\; - \b{Q}\cdot\b{T}\cdot\b{Q}^T\cdot(-\b{Q}\cdot\dot{\b{Q}}^T + \b{Q}\cdot\b{L}^T\cdot\b{Q}^T)\\\;\;\;\;\; = \b{Q}\cdot(\dot{\b{T}}-\b{L}\cdot\b{T}-\b{T}\cdot\b{L}^T)\cdot\b{Q}^T\\\;\;\;\;\; = \b{Q}\cdot\dot{\b{T}}^{(O)}\cdot\b{Q}^T$

Cauchy応力のOldroyd速度には客観性があることがわかる．

Cauchy応力のCotter-Rivelin速度の客観性

$\b{L}^* = \dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{L}\cdot\b{Q}^T = -\b{Q}\cdot\dot{\b{Q}}^T + \b{Q}\cdot\b{L}\cdot\b{Q}^T$

であることを用いて

$\dot{\b{T}}^{(C)*} = \dot{\b{T}}^* + {\b{L}^*}^T\cdot\b{T}^* + \b{T}^*\cdot\b{L}^*\\\;\;\;\;\; = \dot{\b{Q}}\cdot\b{T}\b{Q}^T + \b{Q}\cdot\dot{\b{T}}\b{Q}^T + \b{Q}\cdot\b{T}\dot{\b{Q}}^T\\\;\;\;\;\;\;\; + (-\dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{L}^T\cdot\b{Q}^T)\cdot\b{Q}\cdot\b{T}\cdot\b{Q}^T\\\;\;\;\;\;\;\; + \b{Q}\cdot\b{T}\cdot\b{Q}^T\cdot(\b{Q}\cdot\dot{\b{Q}}^T + \b{Q}\cdot\b{L}\cdot\b{Q}^T)\\\;\;\;\;\; = \b{Q}\cdot(\dot{\b{T}}+\b{L}^T\cdot\b{T}+\b{T}\cdot\b{L})\cdot\b{Q}^T\\\;\;\;\;\; = \b{Q}\cdot\dot{\b{T}}^{(C)}\cdot\b{Q}^T$

Cauchy応力のCotter-Rivelin速度には客観性があることがわかる．

Cauchy応力のGreen-Nargdi速度の客観性

$\b{\Omega}^* = \dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{\Omega}\cdot\b{Q}^T = -\b{Q}\cdot\dot{\b{Q}}^T + \b{Q}\cdot\b{\Omega}\cdot\b{Q}^T$

であることを用いて

$\dot{\b{T}}^{(G)*} = \dot{\b{T}}^* - \b{\Omega}^*\cdot\b{T}^* + \b{T}^*\cdot\b{\Omega}^*\\\;\;\;\;\; = \dot{\b{Q}}\cdot\b{T}\b{Q}^T + \b{Q}\cdot\dot{\b{T}}\b{Q}^T + \b{Q}\cdot\b{T}\dot{\b{Q}}^T\\\;\;\;\;\;\;\; - (\dot{\b{Q}}\cdot\b{Q}^T + \b{Q}\cdot\b{\Omega}\cdot\b{Q}^T)\cdot\b{Q}\cdot\b{T}\cdot\b{Q}^T\\\;\;\;\;\;\;\; + \b{Q}\cdot\b{T}\cdot\b{Q}^T\cdot(-\b{Q}\cdot\dot{\b{Q}}^T + \b{Q}\cdot\b{\Omega}\cdot\b{Q}^T)\\\;\;\;\;\; = \b{Q}\cdot(\dot{\b{T}}-\b{\Omega}\cdot\b{T}+\b{T}\cdot\b{\Omega})\cdot\b{Q}^T\\\;\;\;\;\; = \b{Q}\cdot\dot{\b{T}}^{(G)}\cdot\b{Q}^T$

Cauchy応力のGreen-Nargdi速度には客観性があることがわかる．

Kirchhoff応力の各種速度の客観性

$\tr\b{D}^* = \tr(\b{Q}\cdot\b{D}\cdot\b{Q}^T) = \tr(\b{Q}\cdot\b{Q}^T\cdot\b{D}) = \tr\b{D}$

$(\b{T}\tr\b{D})^* = \b{Q}\cdot\b{T}\cdot\b{Q}^T\tr\b{D} = \b{Q}\cdot(\b{T}\tr\b{D})\cdot\b{Q}^T$

よって $\b{T}\tr\b{D}$ には客観性があることがわかる．そこで相対Kirchhoff応力の各種速度について

$\{\begin{array}{l}\dot{\hat{\b{T}}}^{(J)} = \dot{\b{T}}^{(J)} + \b{T}\tr\b{D}\\ \dot{\hat{\b{T}}}^{(O)} = \dot{\b{T}}^{(O)} + \b{T}\tr\b{D}\\ \dot{\hat{\b{T}}}^{(G)} = \dot{\b{T}}^{(G)} + \b{T}\tr\b{D}\\ \dot{\hat{\b{T}}}^{(C)} = \dot{\b{T}}^{(C)} + \b{T}\tr\b{D}\end{array}$

が成り立ち、 $\dot{\b{T}}^{(J)},\;\dot{\b{T}}^{(O)},\;\dot{\b{T}}^{(G)},\;\dot{\b{T}}^{(C)}$ はそれぞれ客観性をもつので、相対kirchhoff応力の各種速度 $\dot{\hat{\b{T}}}^{(J)},\;\dot{\hat{\b{T}}}^{(O)},\;\dot{\hat{\b{T}}}^{(G)},\;\dot{\hat{\b{T}}}^{(C)}$ もまた客観性を持つ．

Truesdell応力速度 $\dot{\b{S}}_t$ は相対Kirchhoff応力のOldroyd速度 $\dot{\hat{\b{T}}}^{(O)}$ に等しかったので客観性を持つ．

参考にしたもの

Books

非線形有限要素法のためのテンソル解析の基礎	久田俊明　(著)
非線形有限要素法の基礎と応用	久田俊明, 野口裕久 (著)
Nonlinear Finite Elements for Continua and Structures	Ted Belytschko, Wing Kam Liu, Brian Moran(著)
Computational Inelasticity	J. C. Simo, Thomas J. R. Hughes (著)

Made by Nobuyuki UMETANI 梅谷　信行

n.umetani@gmail.com

Stress Rate

目次

概要

Cauchy応力の各種速度

Cauchy応力の各種速度

Cauchy応力のJauman速度

Cauchy応力のGreen-Naghdi速度

Cauchy応力のOldroyd速度

Cauchy応力のCotter-Rivelin速度

各種応力速度の関係

相対Kirchhoff応力の速度

相対Kirchhoff応力のJauman速度

相対Kirchhoff応力のOldroyd速度

相対Kirchhoff応力のCotter-Rivelin速度

相対Kirchhoff応力のGreen-Nargdi速度

Truesdellの応力速度

まとめ

応力速度の客観性

各種テンソルの客観性

Cauchy応力

変形勾配テンソル

速度勾配テンソル

歪み速度テンソル

回転速度テンソル

剛体回転速度テンソル

Cauchy応力を時間微分したテンソルに客観性がない

Cauchy応力の各種速度の客観性

Cauchy応力のJauman速度の客観性

Cauchy応力のOldroyd速度の客観性

Cauchy応力のCotter-Rivelin速度の客観性

Cauchy応力のGreen-Nargdi速度の客観性

Kirchhoff応力の各種速度の客観性

参考にしたもの

Links

Books