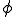 ,ベクトル
,ベクトル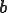 ,テンソル
,テンソル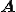 などの場を表す任意の量を
などの場を表す任意の量を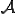 とする
とする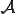 は位置と時刻のみの関数であり,全微分すると以下のように表される.
は位置と時刻のみの関数であり,全微分すると以下のように表される.|TOP Page|
スカラー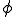 ,ベクトル
,ベクトル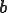 ,テンソル
,テンソル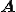 などの場を表す任意の量を
などの場を表す任意の量を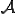 とする
とする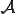 は位置と時刻のみの関数であり,全微分すると以下のように表される.
は位置と時刻のみの関数であり,全微分すると以下のように表される.
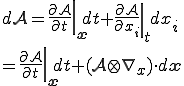
但し,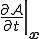 は座標
は座標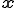 上での
上での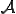 が時間とともに変化する速度であり,空間時間導関数(spatial time derivative)と呼ばれる
が時間とともに変化する速度であり,空間時間導関数(spatial time derivative)と呼ばれる
| 空間時間導関数 |
|---|
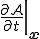 |
ここで,物質点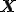 上での微小な時間
上での微小な時間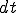 における
における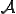 の変化量
の変化量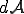 を求める.
を求める.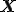 は物質点のラベルであり,物質点
は物質点のラベルであり,物質点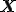 上の
上の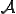 が時間とともに変化する速度を
が時間とともに変化する速度を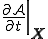 のように表す.上式は物質時間導関数(material time derivative)と呼ばれる.
のように表す.上式は物質時間導関数(material time derivative)と呼ばれる.
| 物質時間導関数 |
|---|
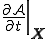 |
物質点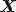 の座標を
の座標を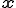 とする.物質点の座標
とする.物質点の座標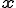 は時刻
は時刻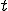 のみの関数であるから,全微分をすると
のみの関数であるから,全微分をすると
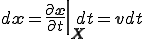
ここで は物質点の速度である.これを上式に代入すると,
は物質点の速度である.これを上式に代入すると,
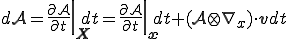
よって次の物質時間導関数と空間時間導関数との関係が得られる
| 物質時間導関数と空間時間導関数の関係 |
|---|
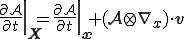 |
![d\dot{v} = \dot{J}dV\\ = {\Big(\big[\quad d{\b{x}_1} \quad d{\b{x}_2} \quad d{\b{x}_3} \quad \big]\Big)}^{.}\\ = {\Big(\big[\quad {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \big]\Big)}^{.}\\ = \left[ \quad \dot{\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right] \quad + \left[ \quad {\b{F}} \cdot d{\b{X}_1} \quad \dot{\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right] \quad + \left[\quad {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad \dot{\b{F}} \cdot d{\b{X}_3} \quad \right]\\ = \left[\quad ( \dot{\b{F}} \cdot {\b{F}^{-1}} ) \cdot {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right] \quad + \left[ \quad {\b{F}} \cdot d{\b{X}_1} \quad ( \dot{\b{F}} \cdot {\b{F}^{-1}} ) \cdot {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right]\\ \qquad \qquad \qquad \qquad \qquad + \left[ \quad {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad ( \dot{\b{F}} \cdot {\b{F}^{-1}} ) \cdot {\b{F}} \cdot d{\b{X}_3} \quad \right]\\ = \tr({\b{F}^{-1}} \cdot {\b{F}} ) \left[ \quad {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right]\\ = (\tr{\b{L}})(\det{\b{F}})\left[ \quad d{\b{X}_1} \quad d{\b{X}_2} \quad d{\b{X}_3}\quad \right]\\ = (\nabla_x \cdot {\b{v}})JdV d\dot{v} = \dot{J}dV\\ = {\Big(\big[\quad d{\b{x}_1} \quad d{\b{x}_2} \quad d{\b{x}_3} \quad \big]\Big)}^{.}\\ = {\Big(\big[\quad {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \big]\Big)}^{.}\\ = \left[ \quad \dot{\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right] \quad + \left[ \quad {\b{F}} \cdot d{\b{X}_1} \quad \dot{\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right] \quad + \left[\quad {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad \dot{\b{F}} \cdot d{\b{X}_3} \quad \right]\\ = \left[\quad ( \dot{\b{F}} \cdot {\b{F}^{-1}} ) \cdot {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right] \quad + \left[ \quad {\b{F}} \cdot d{\b{X}_1} \quad ( \dot{\b{F}} \cdot {\b{F}^{-1}} ) \cdot {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right]\\ \qquad \qquad \qquad \qquad \qquad + \left[ \quad {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad ( \dot{\b{F}} \cdot {\b{F}^{-1}} ) \cdot {\b{F}} \cdot d{\b{X}_3} \quad \right]\\ = \tr({\b{F}^{-1}} \cdot {\b{F}} ) \left[ \quad {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right]\\ = (\tr{\b{L}})(\det{\b{F}})\left[ \quad d{\b{X}_1} \quad d{\b{X}_2} \quad d{\b{X}_3}\quad \right]\\ = (\nabla_x \cdot {\b{v}})JdV](436F6E74696E756D204D656368616E69637320666F7220466C756964_eq0028.gif)
よってヤコビアンの速度には次の式が成り立つ
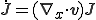
これはEularの膨張公式と呼ばれる.
| Eularの膨張公式 |
|---|
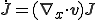 |
物質中の任意の領域を考える.この領域の中のすべての物質点は時間が経過してもこの領域の中にあるとする.つまり,この領域は時間が経過するとともに物質点の速度にしたがって形を変化させる.このような領域を物質検査体積(material control volume)と呼ぶ.この領域内でのある物理量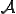 の総和の時間とともに変化する速度を記述したものがReynoldsの輸送方程式(Reynolds transport theorem)である.Reynoldsの輸送方程式を用いることによって,連続の式(continuity equation),運動方程式(momentum equation),エネルギー方程式(energy equation)などを導くことができる.
の総和の時間とともに変化する速度を記述したものがReynoldsの輸送方程式(Reynolds transport theorem)である.Reynoldsの輸送方程式を用いることによって,連続の式(continuity equation),運動方程式(momentum equation),エネルギー方程式(energy equation)などを導くことができる.
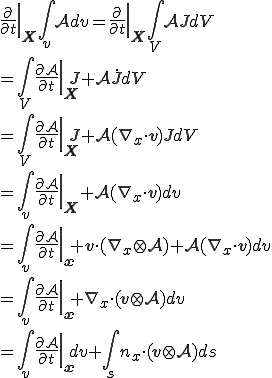
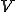 は初期配置における領域である.最初の式では微分のオペレータが領域
は初期配置における領域である.最初の式では微分のオペレータが領域 にもかかっていたため,領域境界の変形する速度も考慮する必要があったが,それを一度,時刻
にもかかっていたため,領域境界の変形する速度も考慮する必要があったが,それを一度,時刻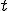 に依存しない初期配置における領域に変換し,もう一度現配置に戻すすることによって,領域境界の速度には依存しない式に書き換えている.但し,次の現配置から基準配置への体積変換変換式,ヤコビアン
に依存しない初期配置における領域に変換し,もう一度現配置に戻すすることによって,領域境界の速度には依存しない式に書き換えている.但し,次の現配置から基準配置への体積変換変換式,ヤコビアン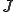 の速度に関する式を用いた
の速度に関する式を用いた
![dv = \left[\quad d{\b{x}_1} \quad d{\b{x}_2} \quad d{\b{x}_3} \quad \right]\\ = \left[\quad {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right]\\ = (\det{\b{F}})\left[ \quad d{\b{X}_1} \quad d{\b{X}_2} \quad d{\b{X}_3} \quad \right]\\ = JdV dv = \left[\quad d{\b{x}_1} \quad d{\b{x}_2} \quad d{\b{x}_3} \quad \right]\\ = \left[\quad {\b{F}} \cdot d{\b{X}_1} \quad {\b{F}} \cdot d{\b{X}_2} \quad {\b{F}} \cdot d{\b{X}_3} \quad \right]\\ = (\det{\b{F}})\left[ \quad d{\b{X}_1} \quad d{\b{X}_2} \quad d{\b{X}_3} \quad \right]\\ = JdV](436F6E74696E756D204D656368616E69637320666F7220466C756964_eq0037.gif)
このReynoldsの輸送定理を使って積分形式の式を微分形式に変換する時には,物質検査体積を任意にとれることから被積分関数における式が常に成り立つということをよく使う.
物体の質量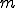 は質量密度
は質量密度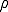 ,物体の閉める領域を
,物体の閉める領域を として
として
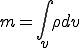
により与えられる.質量保存の原理(principle of conservation of mass)とは物質の質量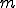 が時間に依存せず変形後も一定,すなわち
が時間に依存せず変形後も一定,すなわち
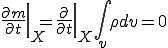
が成立することを述べている.この積分形式でかかれた質量保存の原理の微分形式,すなわち連続の式を求める
Reynoldsの輸送方程式の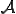 に
に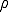 を代入すると次の式が得られる
を代入すると次の式が得られる
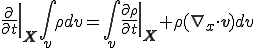
よって,
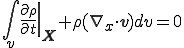
これが任意の領域 に対して成り立つので,
に対して成り立つので,
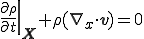
が成り立つ.これは連続の式のLagrange表示と呼ばれる.
| 連続の式のLagrange表示 |
|---|
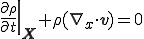 |
さらに,Reynoldsの輸送方程式の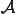 に
に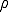 を代入すると次の式が得られる
を代入すると次の式が得られる
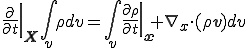
これが任意の領域 に対して成り立つので,
に対して成り立つので,
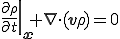
が成り立つ.これは連続の式のEular表示と呼ばれる.
| 連続の式のEular表示 |
|---|
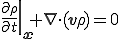 |
運動量などの量の輸送では輸送される量が密度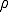 に比例する。このような場合には特別簡単な式が成り立つ。
に比例する。このような場合には特別簡単な式が成り立つ。
連続の式を用いて輸送される物理量が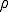 に比例し
に比例し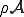 と表せる場合について以下のように変形できる。
と表せる場合について以下のように変形できる。
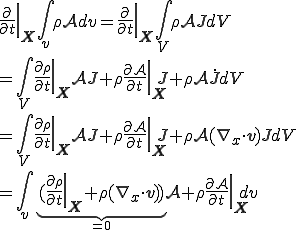
Lagrange型の連続の式より上式右辺第1項が0であるから最終的に
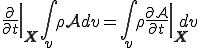
となり,(物質)時間導関数を積分の中に含めることができる.
ここで,質量保存の原理が基準配置を用いてどのように表せられるかについて調べる.質量保存の原理から基準座標の密度を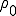 とすると
とすると
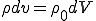
となる.さらに上式から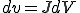 であるから,次の関係式が成り立つ.
であるから,次の関係式が成り立つ.
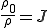
Eularの第1法則(運動量保存の法則)より
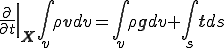
Reynoldsの輸送定理の特別な場合,つまり上式の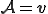 を代入すると
を代入すると
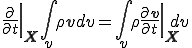
が成り立つ.左辺についても第2項に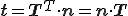 を代入してガウスの発散定理を適応すると
を代入してガウスの発散定理を適応すると
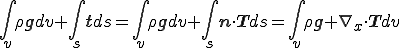
上式を上式に代入すると次の式が得られる.
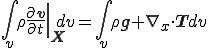
この式が任意の領域 に対して成立するので
に対して成立するので
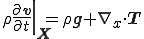
が成り立つ,これはCauchyの第一運動法則と呼ばれる.
| Cauchyの第一運動法則 |
|---|
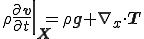 |
左辺第1項の物質時間導関数を空間時間導関数に変えると
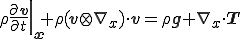
となり,Eular座標系で記述されたCauchyの第一運動法則が得られる.
| Eular座標系で記述されたCauchyの第一運動法則 |
|---|
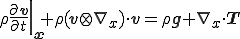 |
角運動量(angular momentum)の保存に関しては次の原理が成立する.すなわち,座標の原点に関して物体力及び表面力のモーメントと運動量モーメント(moment of momentum)の速度が次のように等値される.
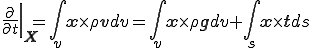
これはEularの第2運動法則(Eular's second law of motion)と呼ばれる.左辺でReynoldsの輸送定理の特殊な場合,つまり上式で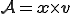 ,及び
,及び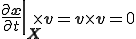 を考慮すると次式を得る.
を考慮すると次式を得る.
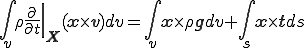
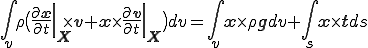
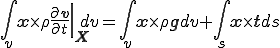
右辺第2項について式変形すると
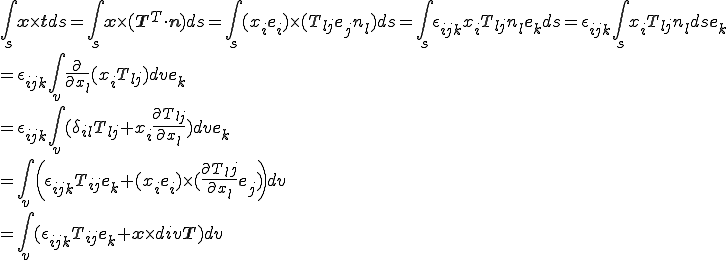
これを上式に代入すると
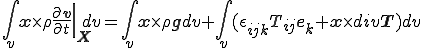
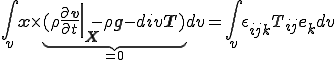
Cauchyの第一運動法則を左辺第一項に適応すると左辺は0となるので最終的に以下の等式が成り立つ.
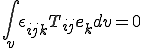
つまり,
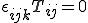
を得る.上式が成立するためには
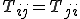
すなわち
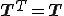
でなくてはならない.よってCauchy応力は対称であり,独立な成分の数は6個となる.上式はCauchyの第二運動法則(Cauchys second law of motion)と呼ばれる.
| Cauchyの第二運動法則 |
|---|
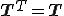 |
| 非線形有限要素法のためのテンソル解析の基礎 | 久田俊明 著 |
| 「連続体力学―簡明な理論と例題」 | P.チャドウィック 著 |