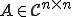 は次のようにユニタリー行列
は次のようにユニタリー行列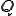 を用いて、上三角行列
を用いて、上三角行列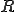 に変換することができる。
に変換することができる。|TOP Page|
QR法とはQR分解を用いて反復的に固有値を求める方法である。
行列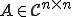 は次のようにユニタリー行列
は次のようにユニタリー行列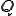 を用いて、上三角行列
を用いて、上三角行列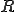 に変換することができる。
に変換することができる。
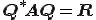
これをシュール分解(Schur Decomposition)という。
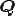 はユニタリー行列なので、
はユニタリー行列なので、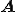 の固有値は
の固有値は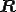 の固有値に等しい。上三角行列
の固有値に等しい。上三角行列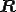 の固有値はその対角成分である。よって
の固有値はその対角成分である。よって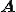 の固有値を調べるためにはシュール分解した上三角行列
の固有値を調べるためにはシュール分解した上三角行列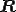 の対角成分を調べればいいことがわかる。
の対角成分を調べればいいことがわかる。
但し、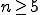 の場合はアベールの定理(Abel's theorem)により、
の場合はアベールの定理(Abel's theorem)により、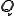 は直接求められないことが知られている。
は直接求められないことが知られている。
そこで反復的な計算により、にシュール分解を行うのがQR法である。
ここで、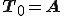 として、
として、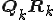 を
を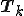 のQR分解であるとする。
のQR分解であるとする。
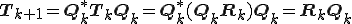 の操作を繰り返す。
の操作を繰り返す。
つまり、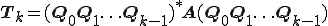
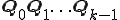 はユニタリー行列であるから、
はユニタリー行列であるから、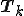 の固有値と
の固有値と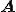 の固有値は等しい
の固有値は等しい
このとき、
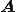 の固有値が実数の場合
の固有値が実数の場合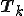 はシュール分解における上三角行列に収束する。
はシュール分解における上三角行列に収束する。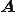 の固有値が複素数の場合
の固有値が複素数の場合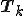 は次のような形に収束する
は次のような形に収束する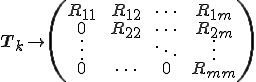
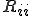 は実数か、互いに共役な複素数の固有値を持つ次元数が2の行列である。
は実数か、互いに共役な複素数の固有値を持つ次元数が2の行列である。
一般的にQR分解は大きな手間を要する。そこで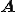 の固有値を変化させない、
の固有値を変化させない、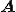 より成分の少ない行列に変換することで計算を大幅に削減することができる。対称行列ならLanczos方を用いて固有値を変えることなく3重対角行列に相似変換できる。また、非対称行列はArnoldi法を用いることでヘッセンベルグ行列に変換できるほか、Two-Sided Lanczos Methodを用いることで3重対角行列に相似変換することができる。このような方法をReductionという。
より成分の少ない行列に変換することで計算を大幅に削減することができる。対称行列ならLanczos方を用いて固有値を変えることなく3重対角行列に相似変換できる。また、非対称行列はArnoldi法を用いることでヘッセンベルグ行列に変換できるほか、Two-Sided Lanczos Methodを用いることで3重対角行列に相似変換することができる。このような方法をReductionという。
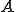 をヘッセンベルグ行列
をヘッセンベルグ行列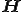
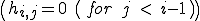 に変換してからQR法を適応すると比較的簡単にQR分解を適応することができる。
に変換してからQR法を適応すると比較的簡単にQR分解を適応することができる。
Arnoldi法を用いると次のように正規直交なベクトル列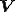 を使って
を使って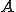 は次のようにヘッセンベルグ行列
は次のようにヘッセンベルグ行列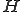 に変換できる。
に変換できる。
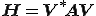
ヘッセンベルグ行列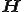 の固有値はRitz値と呼ばれ,と
の固有値はRitz値と呼ばれ,と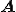 の固有値に近い
の固有値に近い
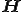 の固有値分布を求めることで、
の固有値分布を求めることで、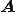 の固有値分布を大方知ることができる.
の固有値分布を大方知ることができる.
ヘッセンベルグ行列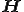 をQR分解する方法はギブンス回転がよく使われる。
をQR分解する方法はギブンス回転がよく使われる。
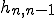 が十分小さくなったら, (n - 1) × (n - 1) 行列の部分の固有値を求めればよい.
が十分小さくなったら, (n - 1) × (n - 1) 行列の部分の固有値を求めればよい.
そうすることで次数を減らすことができ、計算を加速することができる。
次のようにあるシフト量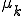 を導入して、求めた
を導入して、求めた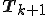 もまた
もまた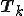 と同じ固有値を持つ
と同じ固有値を持つ
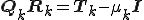
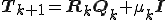
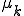 を選ぶことによって収束を加速することができる。
を選ぶことによって収束を加速することができる。
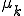 は右下の2×2の行列の固有値のうち、一番右下の対角成分に近いものがよく使われる。これをウィルキンソンの移動法(Wilkinson's Shift)という。
は右下の2×2の行列の固有値のうち、一番右下の対角成分に近いものがよく使われる。これをウィルキンソンの移動法(Wilkinson's Shift)という。