Conjugate Gradient (CG)

共役勾配法,CG法

Last Update:2009年05月15日

概要

CG法(Conjugate Gradient Methods)はM.R.HestenesとE.Stiefelによって1952年に提案された方法である[1]。

CG法は正定値対称行列に対して使われる連立一次方程式を反復法で解くための手法である。

行列の正値対称性

ベクトル u,v の内積を (u,v) のように書く。

実行列 $\b{A}$ が正定値対称とは、 $(\b{A}\b{u},\b{u})\ge0 \quad \forall\b{u}\in\b{R}^n \quad (\quad equal \quad only \quad if \quad \b{u}=0 \quad )$

ということであり、 $\b{A}$ が対称であるということは、

$(\b{A}\b{a},\b{b})=(\b{a},\b{A}\b{b}) \quad \forall\b{a},\b{b}\in\b{R}^n$

が成り立つということである。

ＣＧ法の基本原理

今、次のような線形同次方程式 $\b{A}\b{x}=\b{b}$ を解くとする。

CG法は回目の反復において、次のようにこの方程式の解 $\b{x }$ や誤差 $\b{e}$ を用いて定義される誤差の $\b{A}$ ノルム

$||\b{e}||_A^2=(\b{e},\b{A}\b{e})=||\b{x}_k-\b{x}||_A^2=$\b{x}_k-\b{x},\b{A}(\b{x}_k-\b{x})$\ge0\quad$ (等号成立は $\b{x}_k=\b{x}$ のとき)

を最小化するような近似解 $\b{x}_k$ を部分空間 $\cal{K}_k+\b{x}_0$ の中から見つける方法である。但し、 $\cal{K}_k$ はクリロフ部分空間(Krylov Subspace) $\b{\cal{K}}_k=span\{\b{r}_0,\b{A}\b{r}_0,\b{A}^2\b{r}_0,\cdots,\b{A}^{k-1}\b{r}_0\}$ である。

つまりCG法は次のような連立一次方程式の近似解 $\b{x}_k$ を探すための方法である。

$find \quad \b{x}_k\in\b{x}_0+\b{\cal{K}}_k\quad that \quad minimize ||\b{x}-\b{x}_k||_A$

このように部分空間 $\cal{K}_k+\b{x}_0$ の中で $\b{x}$ との $\b{A}$ ノルムで表される距離が極値をとるとき、明らかに次のような直交性の関係が成り立つ。

$(\b{x}_k-\b{x},\b{w})_{\b{A}} = 0 \qquad \qquad \forall\b{w}\in\cal{K}_k$

但し、行列によって定義される内積 $(\b{a},\b{b})_{\b{A}}=(\b{A}\b{a},\b{b})$ とした。これを用いるとCG法は次のように表すことができる。

$find \quad \b{x}_k\in\b{x}_0+\cal{K}_k \qquad so \quad that \qquad \qquad \b{x}_k-\b{x}\quad\bot_{\b{A}}\quad\cal{K}_k$

但し $\bot_{\b{A}}$ とは次の関係を表している。 $\b{a}\quad\bot_{\b{A}}\quad\b{b} \Leftrightarrow (\b{a},\b{b})_{\b{A}}=0 \Leftrightarrow (\b{A}\b{a},\b{b})=0\Leftrightarrow \b{A}\b{a} \bot \b{b}$

つまりCG法は解 $\b{x}$ を部分空間 $\cal{K}_k+\b{x}_0$ に行列により定義される内積において正射影する方法であるともいえる。クリロフ部分空間 $\cal{K}_k$ は有限次元部分空間であるから、完備な線形空間である。よってLax-Milgramの定理より、このような射影は常に存在する。

(ユークリッド空間で表した)ＣＧ法の反復解の様子

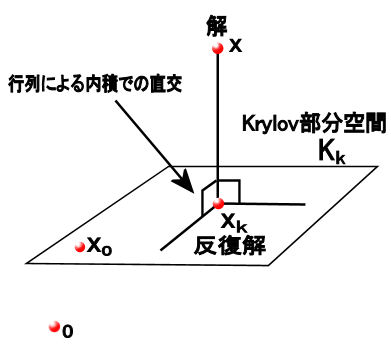また、回反復時における残差 $\b{r}_k$ は $\b{r}_k=\b{A}(\b{x}_k-\b{x})$ であるから、CG法は次のように解を探すともいえる。

$find \quad \b{x}_k\in\b{x}_0+\cal{K}_k \qquad so \quad that \qquad \qquad \b{r}_k\quad\bot\quad\cal{K}_k$

これは残差 $\b{r}_k$ が部分空間 $\cal{K}_k$ に直交するように、 $\cal{K}_k+\b{x}_0$ の中から解を探すということを意味している。

CG法はクリロフ部分空間の正規直交基底を作る方法である、Lanczos法と深い関係にある。

基本的な手続き

解の増分

回目の反復解 $\b{x}_{k}$ から k+1 回目の反復解 $\b{x}_{k+1}$ への解の増分を係数 $\alpha_k$ とベクトル $\b{p}_k$ を用いて次のように書くとする。

$\b{x}_{k+1}-\b{x}_{k}=\alpha_{k}\b{p}_{k}$

$\b{p}$ は解の増分の方向を決めることから探索方向ベクトルと呼ぶ。

k+2 回目の反復解 $\b{x}_{k+2}$ への解の更新ベクトル $\b{p}_{k+1}$ は次のように解 $\b{x}_{k+1}$ の残差 $\b{r}_{k+1}$ 、係数 $\beta_k$ 、１つ前の解の更新ベクトル $\b{p}_k$ を用いて次のように決定する

$\b{p}_{k+1}=\b{r}_{k+1}+\beta_k\b{p}_k$

係数 $\beta$ 、 $\alpha$ をどのように決定するのかを以下で説明する。

係数 $\beta$ の決定

前の議論からCG法では厳密解 $\b{x}$ と反復解 $\b{x}_{k+1}$ の差がクリロフ部分空間 $\cal{K}_{k+1}$ に $\b{A}$ ノルムにおいて直交していた。つまり、

$\b{x}_{k+1}-\b{x}\quad\bot_{\b{A}}\quad\cal{K}_{k+1}$

よって厳密解との差 $\b{x}_{k+1}-\b{x}$ がクリロフ部分空間 $\cal{K}_{k+1}$ と $\b{A}$ ノルムにおいて直交する空間の中にあるのだから、この $\cal{K}_{k+1}$ に $\b{A}$ ノルムで直交する空間の中から次の反復解 $\b{x}_{k+2}$ への解の更新ベクトル $\b{p}_{k+1}$ を決めたほうが $\b{x}_{k+2}$ が厳密解に近くなるはずである。

後に示すように $\b{p}_{k+1}$ の１つ前の探索方向ベクトル $\b{p}_k$ は直交させようとする部分空間 $\cal{K}_{k+1}$ に入っている。つまり、

$\b{p}_k\in\cal{K}_{k+1}$

よって、探索方向ベクトル $\b{p}_{k+1}$ が $\cal{K}_{k+1}$ に $\b{A}$ ノルムで直交するためには最低 $\b{p}_k$ に $\b{A}$ ノルムで直交することが必要条件である。つまり、

$(\b{p}_{k+1},\b{p}_k)_{\b{A}}=(\b{p}_{k+1},\b{A}\b{p}_k)=0$

後に示すように、上のように選んだ探索方向は $\b{p}_{k}$ だけでなく、 $\cal{K}_{k+1}$ 空間に $\b{A}$ ノルムで直交する。

上の残差と１つ前の探索方向ベクトルから探索方向ベクトルを定める式、

$\b{p}_{k+1}=\b{r}_{k+1}+\beta_k\b{p}_k$

から、残差 $\b{r}_{k+1}$ をクリロフ部分空間 $\cal{K}_{k+1}$ と $\b{A}$ ノルムで直交する空間に射影することで新しい探索方向ベクトル $\b{p}_{k+1}$ が得られることを意味している。

またこの式から、 $\beta$ を決定することができる。

この式と２つ探索方向が直交する式 $(\b{p}_{k+1},\b{A}\b{p}_k)=0$ に代入すると、パラメータ $\beta$ は次のようになる。

$\beta=-\frac{(\b{r}_{k+1},\b{A}\b{p}_k)}{(\b{p}_k,\b{A}\b{p}_k)}$

さらに、後に示す残差の直交性の関係式 $(\b{r}_i,\b{r}_j)=0 \quad (\quad i\ne j\quad)$ を用いると、

$(\b{r}_{k+1},\b{A}\b{p}_k)=$\b{r}_{k+1},-\frac{1}{\alpha_k}(\b{r}_{k+1}-\b{r}_k)$=-\frac{1}{\alpha_k}(\b{r}_{k+1},\b{r}_{k+1})$

$(\b{p}_k,\b{A}\b{p}_k)=$\b{r}_k+\beta_{k-1}\b{p}_{k-1},\b{A}\b{p}_k$=$\b{r}_k,\b{A}\b{p}_k$=$\b{r}_k,-\frac{1}{\alpha_k}(\b{r}_{k+1}-\b{r}_k)$=\frac{1}{\alpha_k}(\b{r}_k,\b{r}_k)$

これにより、さらに係数 $\beta_k$ は次の様に表すことができる。

$\beta_k=-\frac{(\b{r}_{k+1},\b{A}\b{p}_k)}{(\b{p}_k,\b{A}\b{p}_k)}=-\frac{-\frac{1}{\alpha_k}(\b{r}_{k+1},\b{r}_{k+1})}{\frac{1}{\alpha_k}(\b{r}_k,\b{r}_k)}=\frac{(\b{r}_{k+1},\b{r}_{k+1})}{(\b{r}_k,\b{r}_k)}$

係数 $\alpha$ の決定

係数 $\alpha$ は次のステップでのポテンシャル $\phi_{k+1}$ を最小化するように決められる。次のステップにおけるポテンシャル $\phi_{k+1}$ は

$\phi_{k+1}=\frac{1}{2}(\b{x}_{k+1},\b{A}\b{x}_{k+1})-(\b{x}_{k+1},\b{f})\\ \quad = \frac{1}{2}\left((\b{x}_k+\alpha\b{p}_k),\b{A}(\b{x}_k+\alpha\b{p}_k)\right)-\left((\b{x}_k+\alpha\b{p}_k),\b{f}\right)\\ \quad = \left{\frac{1}{2}(\b{x}_k,\b{A}\b{x}_k)-(\b{x}_k,\b{f})\right} + \alpha\left{\frac{1}{2}(\b{p}_k,\b{A}\b{x}_k)+\frac{1}{2}(\b{x}_k,\b{A}\b{p}_k)-(\b{p}_k,\b{f})\right} + \alpha^2\left{\frac{1}{2}(\b{p}_k,\b{A}\b{p}_k)\right}\\ \quad = \phi_k+\alpha\left(\b{p}_k,\frac{\b{A}+\b{A}^T}{2}\b{x}_k-\b{f}\right)+\alpha^2\left{\frac{1}{2}(\b{p}_k,\b{A}\b{p}_k)\right}$

行列 $\b{A}$ は対称であったので、 $\frac{\b{A}+\b{A}^T}{2}=\b{A}$ となる。よって

$\phi_{k+1} = \phi_k+\alpha(\b{p}_k,\b{r}_k)+\alpha^2\left{\frac{1}{2}(\b{p}_k,\b{A}\b{p}_k)\right}$

ポテンシャル $\phi_{k+1}$ が最小値をとるとき, ポテンシャル $\phi_{k+1}$ は極値をとるので

$\frac{\partial\phi_{k+1}}{\partial\alpha}=0$

よってこれを計算すると

$(\b{p}_k,\b{r}_k)=\alpha(\b{p}_k,\b{A}\b{p}_k)$

となるので係数 $\alpha$ は次のようになる。

$\alpha=\frac{(\b{p}_k,\b{r}_k)}{(\b{p}_k,\b{A}\b{p}_k)}$

さらに、後に示す残差の直交性の関係式 $(\b{r}_i,\b{r}_j)=0 \quad (\quad i\ne j\quad)$ を用いると、

$(\b{p}_k,\b{r}_k)=(\b{r}_k-\beta_{k-1}\b{p}_{k-1},\b{r}_k)=(\b{r}_k,\b{r}_k)$

これにより、さらに係数 $\alpha_k$ は次の様に表すことができる。

$\alpha_k=\frac{(\b{p}_k,\b{r}_k)}{(\b{p}_k,\b{A}\b{p}_k)}=\frac{(\b{r}_k,\b{r}_k)}{(\b{p}_k,\b{A}\b{p}_k)}$

これらを用いるとCG法のアルゴリズムは次のようになる

アルゴリズム(CG法)

1.   Compute $\b{r}_0=\b{b}-\b{A}\b{x}_0$ , $\b{p}_0=\b{r}_0$
2.   For $k=0,1,\ldots,m\quad$ Do:
3.      $\alpha_k=\frac{(\b{r}_k,\b{r}_k)}{(\b{p}_k,\b{A}\b{p}_k)}$
4.      $\b{x}_{k+1}=\b{x}_k+\alpha_k\b{p}_k$
5.      $\b{r}_{k+1}=\b{r}_k-\alpha_k\b{A}\b{p}_k$
6.      $\beta_k=\frac{(\b{r}_{k+1},\b{r}_{k+1})}{(\b{r}_k,\b{r}_k)}$
7.      $\b{p}_{k+1}=\b{r}_{k+1}+\beta_k\b{p}_k$
8.   $End \quad Do$

********************************

サンプルプログラム

問題の離散化は有限要素法を用いている。

DOWNLOAD	CG.zip

OS:WindowsXP, Windows2000
開発環境:VC++ 2005
言語:C++

収束結果の表示

プログラムを走らせると、プログラムを動かしたフォルダにconv_history.datというファイルができるはずである。これは収束の様子を記録したファイルでgnuplotで次のようなコマンドを打つとグラフとして見ることができる。

set style data line
set logscale y
plot 'conv_history.dat'

次のようなグラフが表示されるはずである。

この収束のグラフについては共役勾配法の収束の中に詳しく書いてある。

クリロフ部分空間とCG法

CG法はクリロフ部分空間法の一種である。クリロフ部分空間法とは、クリロフ部分空間の中でもっとも解に近い近似解を求める方法である。

以下ではCG法がクリロフ部分空間法であることを証明する
ただし部分空間 $\bar{\cal{K}}_k,\tilde{\cal{K}}_k,\cal{K}_k$ については
$\bar{\cal{K}}_k=span\{\b{p}_0,\b{p}_1,\b{p}_2,\cdots,\b{p}_{k-1}\}$
$\tilde{\cal{K}}_k=span\{\b{r}_0,\b{r}_1,\b{r}_2,\cdots,\b{r}_{k-1}\}$
$\cal{K}_k=span\{\b{r}_0,\b{A}\b{r}_0,\b{A}^2\b{r}_0,\cdots,\b{A}^{k-1}\b{r}_0\}$
とする。

$\cal{K}_k=\tilde{\cal{K}}_k=\bar{\cal{K}}_k$ の証明

数学的帰納方を使って証明する

k=1のとき

$\b{r}_0=\b{p}_0$

k>1のとき

$\b{p}_k=\alpha(\b{r}_k+\beta\b{p}_{k-1})$

$\b{p}_k\in\bar{\cal{K}}_{k+1}$

$\b{r}_k\in\tilde{\cal{K}}_{k+1}$

$\b{p}_{k-1}\in\bar{\cal{K}}_k=\tilde{\cal{K}}_k$

$\bar{\cal{K}}_{k+1}=\tilde{\cal{K}}_{k+1}$

$\b{r}_k=\b{r}_{k-1}+\alpha\b{A}\b{p}_{k-1}$

$\b{r}_k\in\tilde{\cal{K}}_{k+1}$

$\b{r}_{k-1}\in\tilde{\cal{K}}_k=\cal{K}_k$

$\b{p}_{k-1}\in\cal{K}_k$

$\b{A}\b{p}_{k-1}\in\cal{K}_{k+1}$

$\tilde{\cal{K}}_{k+1}=\cal{K}_{k+1}$

$\bar{\cal{K}}_{k+1}=\tilde{\cal{K}}_{k+1}=\cal{K}_{k+1}$

以上から数学的帰納法により命題は証明される。

************************************

ところでk回目の反復時における解 $\b{x}_k$ とすると、
$\b{x}_k-\b{x}_0=\sum_{i=0}^{k-1}\Delta\b{x}_i=\sum_{i=0}^{k-1}\alpha_i\b{p}_i$ であるから
$\b{x}_k-\b{x}_0\in\b{\cal{K}}_{k+1}=span\{\b{r}_0,\b{A}\b{r}_0,\b{A}^2\b{r}_0,\cdots,\b{A}^k\b{r}_0\}$ であることがわかる。
よってCG法はクリロフ部分空間の中で解を探索するクリロフ部分空間法であるということがわかる。

以下では残差ｒが直交するという条件からCG法が必ずn解の反復で収束するということを示す。

$(\b{r}_j,\b{p}_i)=0\quad{and}\quad(\b{A}\b{p}_j,\b{p}_i)=0\quad(\quad{for}\quad{0}\le{i}\lt{j}\le{n}\quad)$ の証明

数学的帰納法を使って証明する

k=1のとき

$(\b{r}_1,\b{p}_0) = (\b{r}_0-\alpha\b{A}\b{p}_0,\b{p}_0) = (\b{r}_0,\b{p}_0)-\frac{(\b{r}_0,\b{p}_0)}{(\b{p}_0,\b{A}\b{p}_0)}(\b{A}\b{p}_0,\b{p}_0) = 0$

$(\b{A}\b{p}_1,\b{p}_0) = (\b{A}(\b{r}_1-\beta\b{p}_0),\b{p}_0) = (\b{A}\b{r}_1,\b{p}_0)-\frac{(\b{r}_1,\b{A}\b{p}_0)}{(\b{p}_0,\b{A}\b{p}_0)}(\b{A}\b{p}_0,\b{p}_0) \\ \qquad \qquad \qquad \qquad = (\b{r}_1,\b{A}^T\b{p}_0)-(\b{r}_1,\b{A}\b{p}_0)=0$

$\b{A}$

$\b{A}^T=\b{A}$

k>1のとき

$0\le{i}\lt{j}\le{k}$

$0\le{i}\lt{j}\le{k+1}$

$i\le{k}$

i=kのとき

$(\b{r}_{k+1},\b{p}_i) = (\b{r}_{k+1},\b{p}_k) = (\b{r}_k-\alpha\b{A}\b{p}_k,\b{p}_k) = (\b{r}_k,\b{p}_k)-\frac{(\b{r}_k,\b{p}_k)}{(\b{p}_k,\b{A}\b{p}_k)}(\b{A}\b{p}_k,\b{p}_k)=0$

$(\b{A}\b{p}_{k+1},\b{p}_i) = (\b{A}\b{p}_{k+1},\b{p}_k) = (\b{A}(\b{r}_{k+1}-\beta\b{p}_k),\b{p}_k) = (\b{A}\b{r}_{k+1},\b{p}_k)-\frac{(\b{r}_{k+1},\b{A}\b{p}_k)}{(\b{p}_k,\b{A}\b{p}_k)}(\b{A}\b{p}_k,\b{p}_k) \\ \qquad \qquad \qquad \qquad = (\b{r}_{k+1},\b{A}^T\b{p}_k)-(\b{r}_{k+1},\b{A}\b{p}_k)=0$

i<kのとき

$(\b{r}_{k+1},\b{p}_i) = (\b{r}_k-\alpha\b{A}\b{p}_k,\b{p}_i) = (\b{r}_k,\b{p}_i)-\frac{(\b{r}_k,\b{p}_k)}{(\b{p}_k,\b{A}\b{p}_k)}(\b{A}\b{p}_k,\b{p}_i)=0$

$(\b{A}\b{p}_{k+1},\b{p}_i) = (\b{p}_{k+1},\b{A}\b{p}_i) = (\b{r}_{k+1}-\beta\b{p}_k,\b{A}\b{p}_i) = (\b{r}_{k+1},\b{A}\b{p}_i)-\beta(\b{p}_k,\b{A}\b{p}_i)\\ \qquad \qquad \qquad \qquad = \frac{1}{\alpha}(\b{r}_{k+1},\b{r}_i-\b{r}_{i+1})-\beta(\b{p}_k,\b{A}\b{p}_i)\\ \qquad \qquad \qquad \qquad = \frac{1}{\alpha}\left(\b{r}_{k+1},(\b{p}_i+\beta\b{p}_{i-1})-(\b{p}_{i+1}+\beta\b{p}_i)\right)-\beta(\b{p}_k,\b{A}\b{p}_i)=0$

よってのときでも成立つことから $0\le{i}\lt{j}\le{k+1}$ についても成立つことがわかる

以上から数学帰納法を用いれば命題は証明される

************************************

$(\b{r}_i,\b{r}_j)=0\quad(\quad{for}\quad{0}\le{i}\lt{j}\le{n}\quad)$ の証明

数学的帰納法で証明する

k=1のとき

$(\b{r}_0,\b{r}_1)=(\b{p}_0,\b{r}_1)=0$

k>1のとき

$0\le{i}\lt{j}\le{k}$

$0\le{i}\lt{j}\le{k+1}$

$(\b{r}_i,\b{r}_{k+1}) = (\b{r}_i,\b{r}_k-\alpha\b{A}\b{p}_k) = (\b{r}_i,\b{r}_k)-\alpha(\b{A}\b{p}_k,\b{r}_i) = (\b{r}_i,\b{r}_k)-\alpha(\b{A}\b{p}_k,\b{p}_i+\beta\b{p}_{i-1}) = 0$

よってのときでも成立つことから $0\le{i}\lt{j}\le{k+1}$ についても成立つことがわかる

以上から数学帰納法を用いれば命題は証明される

************************************

ここで残差ベクトルの列 $\b{r}_i$ は互いに直交する線形独立なベクトルであることがわかった。線形独立なベクトルの数の最大値はベクトルの次元数であるので、残差ベクトルの列の数はベクトルの次元数より大きくならないことがわかる。このことから、理論上では

CG法は必ずベクトルの次元数n回以下の反復数で収束する

ということがいえる。但し、これはあくまでこれは理論上の話でCG法は丸め誤差の影響を強くうけるので、計算機上ではCG法はn回の反復で完全に収束することはない。

実用的な収束については共役勾配法の収束の中に詳しく書いてある。

複素数行列におけるCG法

係数が複素数の場合は係数行列は対称行列ではなく、エルミート行列(Hermetian Matrix)でなくてはならない。つまり

A^*=A

この場合にかぎり、内積 (p,Ap) は実数となる。また、固有値も全て実数となる。

係数行列がエルミート行列でなく、対称行列である場合はCOCG法(Conjugate Orhogonal Conjugate Gradient Method)などを使って解くことができる。

またそうでない場合はCGNR法(Conjugate Non-Linear Method)、などを用いて解く。

土屋卓也先生のページ: http://daisy.math.sci.ehime-u.ac.jp/users/tsuchiya/math/linear/variational/index.html

連立1次方程式の基礎知識 九州大学情報基盤研究開発センター研究部、渡部善隆先生による数値解析チュートリアル2004資料: http://yebisu.cc.kyushu-u.ac.jp/~watanabe/RESERCH/MANUSCRIPT/TUTORIAL/leq.pdf

An Introduction to the Conjugate Gradient Method Without the Agonizing Pain California大学Berkeley校Jonathan Shewchuk先生による大変詳しいドキュメント: http://www.cs.cmu.edu/~quake-papers/painless-conjugate-gradient.pdf

Made by Nobuyuki UMETANI 梅谷　信行

n.umetani@gmail.com

Conjugate Gradient (CG)

目次

概要

行列の正値対称性

ＣＧ法の基本原理

基本的な手続き

解の増分

係数 $\beta$ の決定

係数 $\alpha$ の決定

アルゴリズム(CG法)

サンプルプログラム

収束結果の表示

クリロフ部分空間とCG法

$\cal{K}_k=\tilde{\cal{K}}_k=\bar{\cal{K}}_k$ の証明

$(\b{r}_j,\b{p}_i)=0\quad{and}\quad(\b{A}\b{p}_j,\b{p}_i)=0\quad(\quad{for}\quad{0}\le{i}\lt{j}\le{n}\quad)$ の証明

$(\b{r}_i,\b{r}_j)=0\quad(\quad{for}\quad{0}\le{i}\lt{j}\le{n}\quad)$ の証明

複素数行列におけるCG法

参考文献

Wikipedia

Books

Paper

Linkes