 �����
����� ,CoarseGrid�̃I�y���[�^
,CoarseGrid�̃I�y���[�^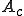 �����
�����|TOP Page|
AMG�@��Multigrid�@�̈��̕��@�ł���A�����i�q�����łȂ��A��\���i�q���ʓI�ȑa�s���������悤�Ɋ}���`�O���b�h�@���g���������̂ł���B�}���`�O���b�h�@�Ɠ������A�����̖��ł͔����������b�V���T�C�Y�Ɉˑ����Ȃ��Ƃ�������������A���݂����Ƃ������ȘA���ꎟ�������̉�@��1�Ƃ�����B
AMG���I�}���`�O���b�h�@�ƈႤ�_�́A
�ł���BAMG�@�ł͍s������������Ƃ��āA
 �����
�����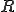 ,CoarseGrid�̃I�y���[�^
,CoarseGrid�̃I�y���[�^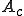 �����
�����Coarse Grid Correction��Smoother�̎������x���悤�Ȍ덷�𗎂Ƃ����Ƃ��ړI�ł���B���̌덷����菜�����߂ɂ�Prolongation�I�y���[�^�̒l��ɂ��̌덷���܂܂�Ă��Ȃ���Ȃ�Ȃ��B����Ă���Smoother�̎������x���悤�Ȍ덷���ǂ̂悤�Ȑ����������Ă���̂��ׂĂ��̂悤�Ȍ덷��\���ł���悤��Prolongation�̃I�y���[�^���쐬����BSmoother�̎������x���悤�Ȍ덷�͎��̂悤�Ȑ����������Ă���B
�ȉ����̏�̐����ɂ��ďڂ����q�ׂ�
�ÓT�I�����@�ɂ�����c���͎��̂悤�ɍX�V�����
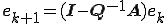
�ÓT�I�����@�Ŏ������x���ꍇ��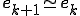 �ł��邩��A
�ł��邩��A
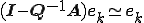
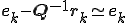
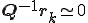
�܂�A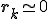
Smoother�Ŏ������x���덷�͎c�����������Ƃ������Ƃ�������B
CoarseGridCorrection�ł͂��̂悤��Smoother�̌�������邢�A�c�����������Ƃ����������������덷�������悭���������邱�Ƃ�ڕW�Ƃ��Ă���B���̂��߁A�c�����������Ƃ��������͔��ɏd�v�ŁA���̒P���Ȑ������������덷���l��ɂ͂���悤��Prolongation�̃I�y���[�^�����߁ACoarseGridCorrection���s���B
���̂悤�ȏ������c���ނ悤�Ȍ덷���㐔�I�Ɋ��炩�Ȍ덷(Algebraically Smooth error)�Ƃ����B���ɂ���đ㐔�I�Ɋ��炩�Ȍ덷�ł��I�ɂ͐U�����Ă���\��������B�܂����̂悤�ɏ����Ȏc���ނ悤�Ȍ덷�̕ʂ̌Ăѕ��Ƃ��Ēl���O�ɋ߂����Ƃ���Near Kernel error�Ƃ������B
��̋c�_�͑�G�c�ŁA�������c���Ƃ͂����Ă����Ɣ�r���ď������̂��킩��Ȃ��B�����Ɛ��m�ɂ́A�Q�̌덷�m�����Ɏ��̊W�����藧�Ƃ��c�����������Ƃ����B
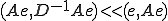 �܂�A
�܂�A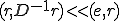
�����ŏ�����
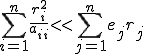
��̎��͘a�ŕ\����Ă��邪�A���ϓI�Ȑ����Ƃ���
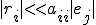
�ƂȂ邱�Ƃ����҂����B
���āA�c�����������܂�A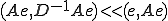 �ł���悤�Ȍ덷�͂ǂ̂悤�Ȑ��������̂��ׂĂ݂悤�B
�ł���悤�Ȍ덷�͂ǂ̂悤�Ȑ��������̂��ׂĂ݂悤�B
���̊W�����藧�B
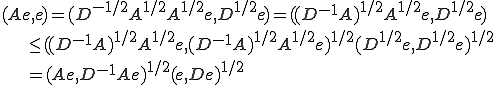
�����ł̓V�������c�̕s������p�����B����𗘗p���āA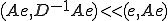 �ł���ꍇ��
�ł���ꍇ��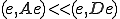 �ł��邱�Ƃ��킩��B
�ł��邱�Ƃ��킩��B
������p���Ă���������Ǝ��̂Ƃ���ɂȂ�B
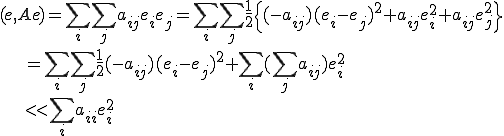
�����ŁA�����̏ꍇ�ɐ��藧��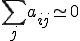 �̊W��p����B�܂��㎮�͘a�ɂ��Đ��藧���ł��邪�A���ϓI�Ȑ����Ƃ��Ċei�ɂ��Ă����藧�Ƃ���Ǝ��̂Ƃ���ɂȂ�B
�̊W��p����B�܂��㎮�͘a�ɂ��Đ��藧���ł��邪�A���ϓI�Ȑ����Ƃ��Ċei�ɂ��Ă����藧�Ƃ���Ǝ��̂Ƃ���ɂȂ�B
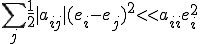
�܂�ȉ������藧��
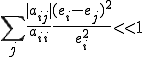 |
�����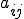 ���傫�����
���傫�����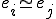 �����藧���Ƃ��Ӗ����Ă���B
�����藧���Ƃ��Ӗ����Ă���B
�܂�A�덷�͋����ڑ���ŋ}���ɕω����Ȃ��Ƃ��������������Ă��邱�Ƃ��킩��B
�傫���P�~�P�̋�`�̈�ɂ����鎟�̂悤�Ȉٕ����̂���|�A�\��������(Poisson's Equation)
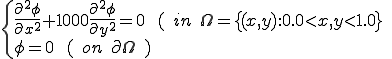
�ɂ����ė����������l�Ƃ���Gauss Sidel�@��p����Smoother��300������������̌덷�̗l�q�ł���B
���̕����������̕����̊g�U�W����1000�{�傫���A�̈�̓����̑S�Ă̓_�͂��̕����ɋ����ڑ��A���̕����Ɏキ�ڑ����Ă���B�������ɂ͉��������_���ɐU�����Ă���̂ɑ��Ă������ɂ͊��炩�ɕω����Ă���BSmoother�Ŏ����̒x���덷�͋����ڑ���ŋ}���ɕω����Ȃ��Ƃ������Ƃ��킩��B
�����ڑ���Ō덷�̕ω������Ȃ��̂ł��̋����ڑ��̕����ɓ_���Ԉ����A��Ԃɂ���ĊԈ����ꂽ�_�̒l��\�����邱�Ƃ��ł���B���̂��Ƃ𗘗p����F/C Splittiong��Prolongation�I�y���^�[�̍쐬���s���B
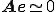 �ł������B���̂Ƃ� �s��
�ł������B���̂Ƃ� �s��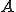 �̐���
�̐���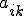 ���傫���ꍇ�A
���傫���ꍇ�A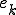 �̒l��
�̒l��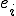 �̒l�ɑ傫���e������B�t��
�̒l�ɑ傫���e������B�t��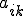 ���������ꍇ�A
���������ꍇ�A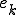 �̒l��
�̒l��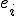 �̒l�ɋy�ڂ��e���͏������Ȃ�B
�̒l�ɋy�ڂ��e���͏������Ȃ�B
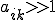 )��k��i��Strong Connection�ł���܂苭���ڑ����Ă���Ƃ����A
)��k��i��Strong Connection�ł���܂苭���ڑ����Ă���Ƃ����A
F/C Spliting��Prolongation�I�y���^�[�쐬���ł͂��̋����ڑ��A�ア�ڑ����͂������ʂ���K�v������B�����ŁAi�s�ڂ̔�Ίp����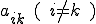 �̑��ΓI�ȑ傫�����画�f���āA�ǂ̐���k��i�ɑ傫���e������̂��ׁA�����ڑ��A�ア�ڑ��ɕ�����B
�̑��ΓI�ȑ傫�����画�f���āA�ǂ̐���k��i�ɑ傫���e������̂��ׁA�����ڑ��A�ア�ڑ��ɕ�����B
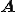 ���l�s��(�Ίp�����Ŕ�Ίp����)�̏ꍇ�͈�ʓI��Strong Connection�͎��̂悤�ɂ��Ē�`�����B
���l�s��(�Ίp�����Ŕ�Ίp����)�̏ꍇ�͈�ʓI��Strong Connection�͎��̂悤�ɂ��Ē�`�����B
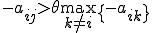
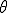 ��
��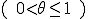 �ł���p�����[�^��0.25�Ƃ���邱�Ƃ������B
�ł���p�����[�^��0.25�Ƃ���邱�Ƃ������B
�}���`�O���b�h�@�ɂ�����Coarce Grid Correction��Smoother���������ɂ����悤�Ȍ덷�𗎂Ƃ����߂̂��̂ł������B
���̂悤�Ȏ������ɂ����덷�̐����Ƃ��āA
�Ƃ������Ƃ����������B���̂悤�Ȍ덷��\���ł���悤��Prolongation�̃I�y���[�^����邱�Ƃ��ڕW�ł���
�������e���O���b�h�̓_�̒l�͂��̂܂ܔ��f�����̂ŁA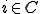 �̂Ƃ�
�̂Ƃ�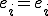 �ł���B�ȉ��ł�
�ł���B�ȉ��ł�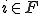 �̂Ƃ��A
�̂Ƃ��A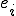 �ǂ̂悤�ɂ��đe���O���b�h�̓_�����Ԃ����̂��ׂ悤�B
�ǂ̂悤�ɂ��đe���O���b�h�̓_�����Ԃ����̂��ׂ悤�B
Smoother�Ŏ������ɂ����덷�͎c���������������B
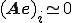
�������Ƃɏ����o���Ǝ��̂悤�ɂȂ�B
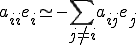
�܂�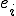 �̒l��
�̒l��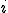 �ɐڑ����Ă���_�S�Ă̒l
�ɐڑ����Ă���_�S�Ă̒l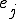 ����m�邱�Ƃ��ł���B�ȉ��ł͂���
����m�邱�Ƃ��ł���B�ȉ��ł͂���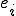 �ɐڑ����Ă���_�̒l�ɂ��ďq�ׂ�B
�ɐڑ����Ă���_�̒l�ɂ��ďq�ׂ�B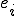 �ɐڑ����Ă���_�͎���3��ނ���B
�ɐڑ����Ă���_�͎���3��ނ���B
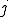
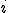 �Ɏキ�ڑ����Ă���ׂ����O���b�h�̓_
�Ɏキ�ڑ����Ă���ׂ����O���b�h�̓_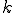
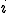 �ɋ����ڑ����Ă���ׂ����O���b�h�̓_
�ɋ����ڑ����Ă���ׂ����O���b�h�̓_
�ׂ����O���b�h�̓_ �ɐڑ����Ă���R��ނ̓_ �ɐڑ����Ă���R��ނ̓_ |
|---|
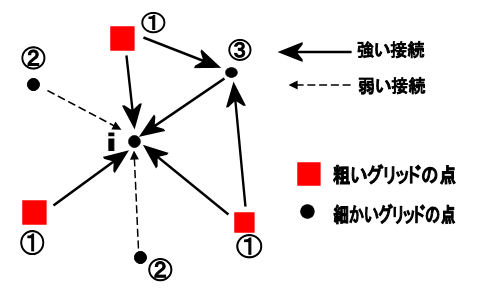 |
| �@�F�e���O���b�h�̓_ �A�Fi�Ɏキ�ڑ����Ă���ׂ����O���b�h�̓_ �B�Fi�ɋ����ڑ����Ă���ׂ����O���b�h�̓_ |
 �ɐڑ����Ă���e���O���b�h�̓_
�ɐڑ����Ă���e���O���b�h�̓_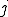 �͒l
�͒l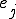 �����̂܂g�������B
�����̂܂g�������B
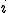 �Ɏキ�ڑ����Ă���ׂ����O���b�h�̓_
�Ɏキ�ڑ����Ă���ׂ����O���b�h�̓_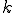
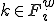 �̏ꍇ�͕�Ԃ��s��Ȃ��B���̂悤�Ȓl���Ƃ邱�Ƃ�CoarseGridCorrection�̈��萫�𑝂����Ƃ��ł���B
�̏ꍇ�͕�Ԃ��s��Ȃ��B���̂悤�Ȓl���Ƃ邱�Ƃ�CoarseGridCorrection�̈��萫�𑝂����Ƃ��ł���B
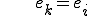
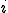 �ɋ����ڑ����Ă���ׂ����O���b�h�̓_
�ɋ����ڑ����Ă���ׂ����O���b�h�̓_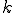
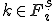 �̏ꍇ�͍s��̌W���̏d�݂�p�������ςƂ��Čv�Z����B
�̏ꍇ�͍s��̌W���̏d�݂�p�������ςƂ��Čv�Z����B
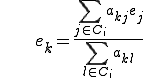
Smoother�Ŏ������ɂ��������͋����ڑ���ŕω������Ȃ��̂ł��̂悤�ɋ����ڑ��Ԃ̕⊮�ɂ���Ēl���ߎ����邱�Ƃ��ł���B���̂悤�ȕ�Ԃ͂�����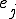 ���萔�ł���ꍇ��
���萔�ł���ꍇ��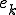 �������l���Ƃ�Ƃ������������B���̂悤�Ȓ萔���[�h�̕�Ԃ��ł��邱�Ƃ͏d�v�ł���B
�������l���Ƃ�Ƃ������������B���̂悤�Ȓ萔���[�h�̕�Ԃ��ł��邱�Ƃ͏d�v�ł���B
���ꂪ�O�ɂȂ�Ȃ��Ƃ�����������A�S�Ă�i�����e�����Ă���_k��i�Ɨאڂ���ׂ����ߓ_l�͕K����͑e���ߓ_�ɗאڂ��Ă��Ȃ���Ȃ�Ȃ��Ƃ������Ƃ��킩��B�ʏ킱�̐��������������悤��F/C Splitting���s��
�ߓ_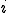 �̎���̓_�̒l�����������̂Őߓ_
�̎���̓_�̒l�����������̂Őߓ_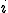 �̒l�����߂Ă݂悤�B
�̒l�����߂Ă݂悤�B
�ߓ_i�ɂ��Ă̎c�����������Ƃ������Ƃ���
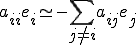
�����藧�̂ł������B���͂̓_�����3�p�^�[���ɕ�����Ǝ��̂悤�ɂȂ�B
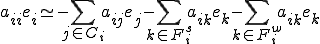
����Ɏ��͂̐ߓ_�̒l�������āA
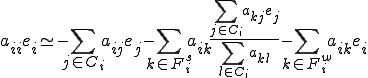
������ό`���Ă܂Ƃ߂��
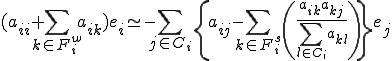
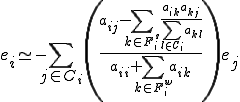
| AMG�ɂ�����e���O���b�h����ׂ����O���b�h�ւ̕�Ԏ� |
|---|
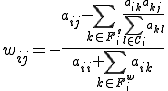 |
![\b{P}=\[W\\I\] \b{P}=\[W\\I\]](416C67656272616963204D756C746967726964204D6574686F6473_eq0077.gif)
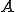 ������l�Ώ̍s��̏ꍇ��Ristriction�̍s��͎��̂悤��Prolongation�̓]�u(
������l�Ώ̍s��̏ꍇ��Ristriction�̍s��͎��̂悤��Prolongation�̓]�u(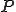 �����f���s��̏ꍇ��Harmetian)��p�����
�����f���s��̏ꍇ��Harmetian)��p�����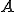 �m�����̈Ӗ��ł̌덷�m�����̍ŏ������ł���B���̂悤�ȕ��@�͗L���v�f�@�Ƃ̗ސ�����Galerkin�@�Ƃ��Ă��
�m�����̈Ӗ��ł̌덷�m�����̍ŏ������ł���B���̂悤�ȕ��@�͗L���v�f�@�Ƃ̗ސ�����Galerkin�@�Ƃ��Ă��
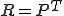
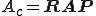
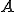 ������l�Ώ̍s��ł͂Ȃ��ꍇ�ɂ�Ristriction��Prolongation�̓]�u��p������@�͕K�������œK�Ƃ͂����Ȃ��B�l�X��Ristriction�����肷����@����Ă���Ă��邪�A���ˑ��ł��邱�Ƃ������B
������l�Ώ̍s��ł͂Ȃ��ꍇ�ɂ�Ristriction��Prolongation�̓]�u��p������@�͕K�������œK�Ƃ͂����Ȃ��B�l�X��Ristriction�����肷����@����Ă���Ă��邪�A���ˑ��ł��邱�Ƃ������B
AMG�@�ł̓R�[�X�O���b�h���s��̌W�������ɍ쐬���Ȃ���Ȃ�Ȃ��B
�ׂ����O���b�h��őe���O���b�h�̓_�̏W����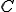 �A����ȊO�̓_��
�A����ȊO�̓_��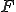 �Ƃ���B
�Ƃ���B
�܂��ׂ����O���b�h�ɂ����ē_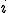 �Ɛڑ����Ă���_
�Ɛڑ����Ă���_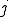 �A�܂�
�A�܂�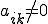 �̏W����
�̏W����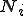 �Ƃ���B
�Ƃ���B
�ׂ����O���b�h��œ_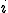 �ɐڑ����Ă���e���O���b�h�̓_�̏W����
�ɐڑ����Ă���e���O���b�h�̓_�̏W����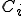 �Ƃ����ӂ��ɏ����B�܂�
�Ƃ����ӂ��ɏ����B�܂�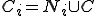
���l�ɍׂ����O���b�h��œ_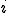 �ɐڑ����Ă���ׂ����O���b�h�̓_�̏W����
�ɐڑ����Ă���ׂ����O���b�h�̓_�̏W����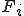 �Ƃ����ӂ��ɏ����B�܂�
�Ƃ����ӂ��ɏ����B�܂�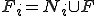
�e���O���b�h�̓_����ׂ����O���b�h�̓_�ɕ�Ԃ��ł��邽�߂ɂ͎��̏��������K�v������B
i���ׂ����O���b�h�̓_�Ƃ��Aj��i�ɋ����ڑ����Ă���_�i�܂�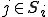 )�Ƃ����j�͑e���_ )�Ƃ����j�͑e���_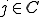 ���A�Œ�P�͑e���_�ɋ����ڑ�( ���A�Œ�P�͑e���_�ɋ����ڑ�(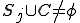 )���Ă��Ȃ���Ȃ�Ȃ� )���Ă��Ȃ���Ȃ�Ȃ� |
�v�Z�����̂��Ƃ��l����Ƃł��邾�����Ȃ��e���O���b�h�̓_�ōׂ����O���b�h�ւ̕�Ԃ��ł����ق��������ƍl������B
��̏��������ł��邾�����Ȃ��O���b�h�Ōv�Z���s�����߂ɂ�
| �e���O���b�h���m�͋����ڑ����Ă��Ȃ� |
�Ƃ����������Ƃ悢�B���̑e���O���b�h���m�̐ڑ����Ȃ��Ƃ��������̓O���b�h�̐������炵�Čv�Z�ʂ�����������Ƃ����ړI�̂��̂ŁA����I�ɏd�v�ȏ����ł͂Ȃ��B
�����ł̓}���`�O���b�h�@�̎����ɂ��ďq�ׂ�B�����ׂ��s��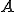 �͐���l�Ώ̂ł���Ƃ���B
�͐���l�Ώ̂ł���Ƃ���B
�܂��ARistriction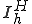 ��Prolongation
��Prolongation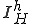 �̓]�u�ł���Ƃ���B�܂�A
�̓]�u�ł���Ƃ���B�܂�A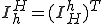
���̏ꍇ���炩�ɃR�[�X�O���b�h�̃I�y���[�^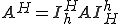 ������l�Ώ̂ł���B
������l�Ώ̂ł���B
�m����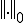 �͎��̂悤�ȃm�����ł���Ƃ���B
�͎��̂悤�ȃm�����ł���Ƃ���B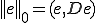 �A�A��
�A�A��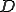 ��
��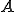 �̑Ίp����
�̑Ίp����
�m����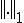 �̓I�y���[�^�[�m�����ł���Ƃ���B�܂�A
�̓I�y���[�^�[�m�����ł���Ƃ���B�܂�A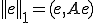
�܂��A�m����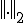 �����̂悤�ɒ�`����
�����̂悤�ɒ�`����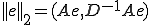
Prolongation�I�y���[�^ �ƃR�[�X�O���b�h�R���N�V�����I�y���[�^
�ƃR�[�X�O���b�h�R���N�V�����I�y���[�^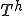 �̒l�悪�I�y���[�^�m����
�̒l�悪�I�y���[�^�m����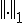 �ɂ��Ē�������A�܂�
�ɂ��Ē�������A�܂�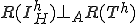 �Ƃ������Ƃ������B
�Ƃ������Ƃ������B
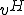 �A
�A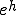 ��C�ӂ̃x�N�g���Ƃ���B
��C�ӂ̃x�N�g���Ƃ���B
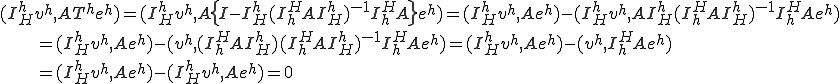
�R�[�X�O���b�h�R���N�V�����̓v�������Q�[�V�����I�y���[�^�̒l��ɃI�y���[�^�m�����ɂ����Ē������镔����Ԃւ̎ˉe�Ƃ������Ƃ��킩��B
�ȏ���
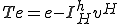
�̗��ӂ�A�m�������v�Z�����
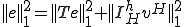
�����藧��
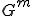 �A �A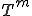 �͂��ꂼ��O���b�h �͂��ꂼ��O���b�h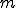 �ɂ�����X���[�U�[�ƃR�[�X�O���b�h�R���N�V�����̃I�y���[�^�ł���Ƃ���B �ɂ�����X���[�U�[�ƃR�[�X�O���b�h�R���N�V�����̃I�y���[�^�ł���Ƃ���B�e�O���b�h 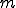 �ɂ��Ĉȉ��̎������藧�Ƃ���� �ɂ��Ĉȉ��̎������藧�Ƃ����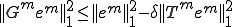 �|�X�g�X���[�W���O�݂̂�Vcycle�}���`�O���b�h�@�ɂ��āA�덷�̃I�y���[�^�m�����̎������� 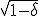 �ŗ}������B �ŗ}������B |
�ȉ��̎��͏������G�Ȃ̂ŁA��̓I�ȗ��p���ĕ����I�ȈӖ����l���悤�B
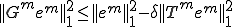
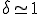 �܂�}���`�O���b�h�@�̎����������Ɖ��肷��ƁA
�܂�}���`�O���b�h�@�̎����������Ɖ��肷��ƁA
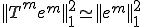 �̏ꍇ�̌덷
�̏ꍇ�̌덷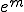 �ɂ��ẮA
�ɂ��ẮA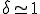 ��薾�炩��
��薾�炩��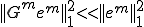 �����藧�B�܂�A�}���`�O���b�h�@���������Ă���ꍇ�́A�R�[�X�O���b�h�R���N�V�����������I�łȂ��덷
�����藧�B�܂�A�}���`�O���b�h�@���������Ă���ꍇ�́A�R�[�X�O���b�h�R���N�V�����������I�łȂ��덷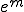 ���X���[�U�[�������I�ɏ��������邱�Ƃ��ł���B
���X���[�U�[�������I�ɏ��������邱�Ƃ��ł���B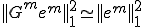 �̏ꍇ�̌덷
�̏ꍇ�̌덷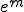 �ɂ��ẮA
�ɂ��ẮA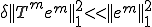 �ł���B������
�ł���B������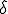 ���P�ɋ߂��Ɖ��肵���̂�
���P�ɋ߂��Ɖ��肵���̂�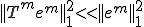 �����藧�B�܂�A�}���`�O���b�h�@���������Ă���ꍇ�́A�X���[�U�[�������I�łȂ��덷
�����藧�B�܂�A�}���`�O���b�h�@���������Ă���ꍇ�́A�X���[�U�[�������I�łȂ��덷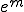 ���R�[�X�O���b�h�R���N�V�����������I�ɏ��������邱�Ƃ��ł���B
���R�[�X�O���b�h�R���N�V�����������I�ɏ��������邱�Ƃ��ł���B�ȏォ�����P�ɋ߂��قǃR�[�X�O���b�h�R���N�V�����ƃX���[�U�[�̔\�͂𑫂����킹�������������Ƃ������Ƃ�������B
�㎮�ɂ�����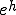 ��
��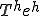 ���������
���������
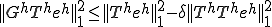
�R�[�X�O���b�h�R���N�V����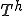 �͎ˉe�I�y���[�^�ł���������A
�͎ˉe�I�y���[�^�ł���������A
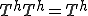 �A
�A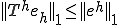 �����藧�B
�����藧�B
������g���Ǝ��̂悤�ɕό`�ł���
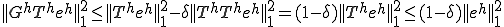
����Ď��̂悤�ɃI�y���[�^�m�����ł̎��������̂悤�ɕ]���ł���B
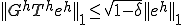
��̃̎����X���[�U�[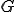 �ƃR�[�X�O���b�h�R���N�V����
�ƃR�[�X�O���b�h�R���N�V����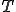 �̃I�y���[�^�ɂ��Ă̂Q�̕����������ɕ�������B
�̃I�y���[�^�ɂ��Ă̂Q�̕����������ɕ�������B
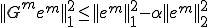 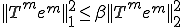 �����藧�ꍇ�� 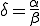 �ł���B �ł���B |
��̎��X���[�U�[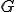 �ɂ��Ă̎���smoothing assumption�Ƃ����A���̃R�[�X�O���b�h�R���N�V����
�ɂ��Ă̎���smoothing assumption�Ƃ����A���̃R�[�X�O���b�h�R���N�V����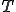 �ɂ��Ă̎���approximation assumption�Ƃ����B
�ɂ��Ă̎���approximation assumption�Ƃ����B
��̎���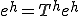 ���������
���������
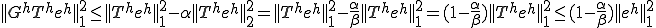
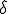 ��p���������̎��ƌ���ׂ��
��p���������̎��ƌ���ׂ��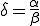 �ł��邱�Ƃ��킩��B
�ł��邱�Ƃ��킩��B
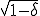 ���|�X�g�X���[�W���O�݂̂�V�T�C�N���}���`�O���b�h�@�̎������a�̏���ł������̂�
���|�X�g�X���[�W���O�݂̂�V�T�C�N���}���`�O���b�h�@�̎������a�̏���ł������̂�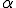 ���傫���A
���傫���A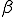 ���������قǎ���������
���������قǎ���������
2cycle multigrid�@�ł́A�C�ӂ�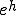 �ɂ��� �ɂ��� 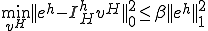 �����藧�Ƃ� �����藧�Ƃ�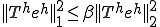 �����藧�� �����藧�� |
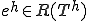 �Ƃ����
�Ƃ����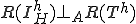 ����A�C�ӂ�
����A�C�ӂ�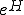 �ɑ��Ĉȉ������藧��
�ɑ��Ĉȉ������藧��
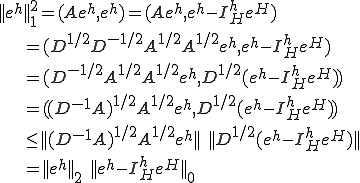
������Shwarz�̕s�����A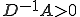 �ł��邱�Ƃ�p�����B
�ł��邱�Ƃ�p�����B
�C�ӂ̔C�ӂ�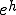 �ɂ���
�ɂ��� 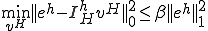 �����藧�Ƃ��A
�����藧�Ƃ��A
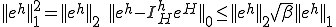
����2�悵��
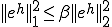
�����藧�B�ȏ��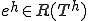 �ɂ��Đ��藧���Ă����̂�
�ɂ��Đ��藧���Ă����̂�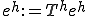 �������čŏI�I��
�������čŏI�I��
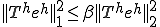
�����藧�B
| Multigrid Methods |
Stephen F.McCormic�@�� |
[1] J.W.Ruge and K.Stuben, algebraic multigrid (AMG), in Mutigrid Methods, S. F. McCormic, ed., Frontiers in Appl. Math. 3, SIAM, Philadelphia, 1987, pp.73-130