|TOP Page|
2次元的な領域で変形する薄肉梁要素について解説する。梁要素とは柱や棒のように細長い構造物を、体積を持たない1次元的な分割によって空間離散化する方法である。つまり要素は断面積や断面に次モーメントなどの量をパラメータとしてもつ。また薄肉とは薄い構造物で成り立つ、Kirhhoff-Loveの仮定が成り立つということである。この仮定は分かり易く言えば、変形前に中立面に垂直な物体の中に埋め込まれたベクトルは変形後でも中立面に垂直ということである。薄肉構造物は面外せん断歪みを持たないので、歪みエネルギーは純粋に曲げによる歪みエネルギーだけとなる。曲げのエネルギーは撓みの2回微分で書くことが出来る。このことが薄肉梁の有限要素法において一般的にエルミート補間が必要であることを解説する。
最終的に求めたいのは非線形の薄肉梁要素であるが、幾つか段階を踏むと理解しやすい。2次元梁要素へのもっとも簡単なステップは、線形曲げ要素である。これは梁をx軸におき、変形を微小なy軸方向のたわみに限定した場合における問題である。次のステップは線形梁要素である。これは線形曲げ要素に梁の軸方向の剛性を加えて、梁の軸方向の変形も取り扱えるようにしたものである。非線形の定式化は、これらを大回転へ発展させて、梁のエネルギーを回転に依存しない形で定義してその微分を計算することで定式化を行う。
静的問題では歪みポテンシャルエネルギーを導出し、その変分としてつりあいの式を導き出す。また動的問題では歪みポテンシャルエネルギーと力学的エネルギーを導出してハミルトンの原理を用いて運動方程式を導き出す。
梁問題を変位法で解析する場合、撓みとその勾配が要素間で連続でなければならないことを示し、もっと単純な例であるエルミート補間について説明する。この補間において梁曲げ要素の定式化を解説する。
次のような両端が変位と回転が固定されているような梁の問題を考えよう
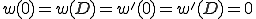
 を曲げ剛性、つまり
を曲げ剛性、つまり (但し
(但し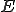 はヤング率
はヤング率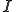 は断面2次モーメント)とするとのように書ける。
は断面2次モーメント)とするとのように書ける。
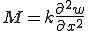
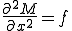
よって、強形式の支配方程式は
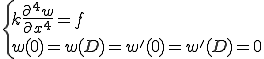
となる。強形式では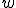 は4回微分可能でなければならない。
は4回微分可能でなければならない。
この問題は次のように弱形式化される
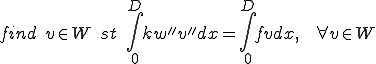
ここで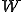 は2階微分が可能で、2階微分がリーマン可積分、つまり2階微分が区分連続であること。それに加えて、境界条件を満たす集合である、つまり
は2階微分が可能で、2階微分がリーマン可積分、つまり2階微分が区分連続であること。それに加えて、境界条件を満たす集合である、つまり
![W=\{\;v\;|\;v\in C[0,D],\; v'\in C[0,D],\; v''\in PC[0,D],\; v(0)=v(D)=v'(0)=v'(D)=0 \;\} W=\{\;v\;|\;v\in C[0,D],\; v'\in C[0,D],\; v''\in PC[0,D],\; v(0)=v(D)=v'(0)=v'(D)=0 \;\}](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0012.gif)
強形式の式が成り立てば弱形式の式が成り立つことを示す。
強形式の式に任意の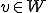 を乗じて、区間
を乗じて、区間![[0,D] [0,D]](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0014.gif) で積分すると、
で積分すると、
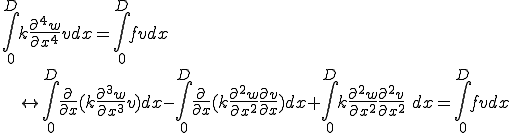
左辺第1,2項は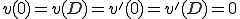 から0になる。よって
から0になる。よって
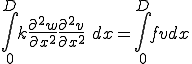
が成り立つ。
区間![I=[0,D] I=[0,D]](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0018.gif) を分割して
を分割して![I_i=[a,b] I_i=[a,b]](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0019.gif) となっていることにしよう。つまり、要素の中で、
となっていることにしよう。つまり、要素の中で、 は
は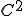 級関数であるとすると、
級関数であるとすると、 の2階微分は区間連続である。さて、
の2階微分は区間連続である。さて、 が連続であるためには、節点を区間要素の両端に置けば、隣合う要素同士で値を共有するので良かった。同様にv'が連続であるためには勾配を表す節点を区間要素の両端に置けばよい。
が連続であるためには、節点を区間要素の両端に置けば、隣合う要素同士で値を共有するので良かった。同様にv'が連続であるためには勾配を表す節点を区間要素の両端に置けばよい。
要素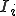 の中で補間関数の2階微分が定数であるとしよう。つまり、要素間で補間関数は3次関数となる。要素
の中で補間関数の2階微分が定数であるとしよう。つまり、要素間で補間関数は3次関数となる。要素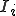 の4つの節点(両端における変位と変位勾配)に対応するアイソパラメトリックな補間関数
の4つの節点(両端における変位と変位勾配)に対応するアイソパラメトリックな補間関数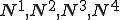 を次のように設定する。
を次のように設定する。
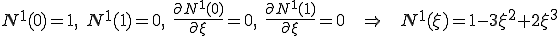
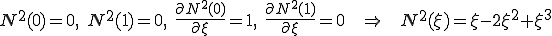
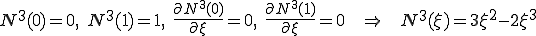
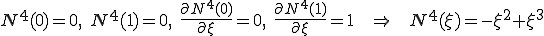
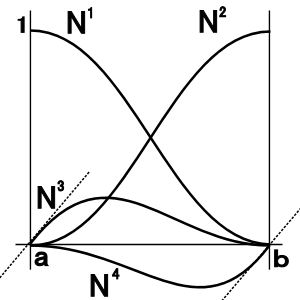 |
この時、要素![I_i=[a_i,b_i] I_i=[a_i,b_i]](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0031.gif) の中の撓みの場は次のようにアイソパラメトリック補間される
の中の撓みの場は次のようにアイソパラメトリック補間される
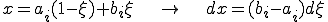
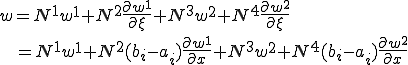
曲げによる歪みエネルギー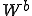 は次のように書くことができる。
は次のように書くことができる。
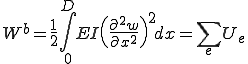
但し、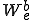 は以下のような要素内の歪みエネルギーである。
は以下のような要素内の歪みエネルギーである。
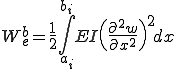
ここで曲げ剛性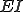 を要素内一定であるとして積分の外にくくりだす。さらに
を要素内一定であるとして積分の外にくくりだす。さらに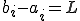 として表記を簡単にする。
として表記を簡単にする。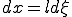 となる。これをもちいて積分と微分の変数変換を行って
となる。これをもちいて積分と微分の変数変換を行って
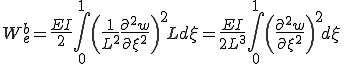
ここで、各補間関数の2回微分は次のとおりであった。
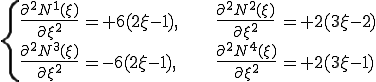
これを代入して
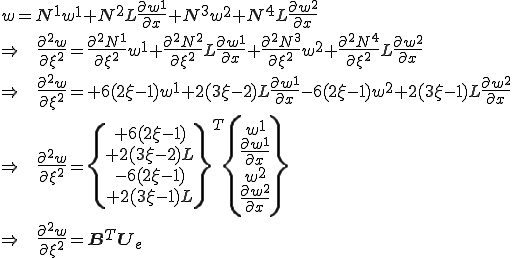
但し,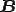 は頂点での変位とその1次微分と一般座標
は頂点での変位とその1次微分と一般座標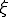 における変位の2回微分を結びつける行列である。
における変位の2回微分を結びつける行列である。
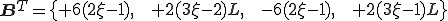
また、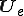 は要素内未知変数ベクトルである。
は要素内未知変数ベクトルである。
これを用いると、曲げエネルギーは次のようになる。
![W^b_e = \frac{EI}{2L^3}\int_0^1\(\frac{\partial^2 w}{\partial \xi^2}\)^2d\xi = \frac{1}{2}\b{U}^T_e\left[ \frac{EI}{L^3}\int_0^1\b{B}\b{B}^T d\xi\right] \b{U}_e = \frac{1}{2}\b{U}_e^T K^b_e \b{U}_e W^b_e = \frac{EI}{2L^3}\int_0^1\(\frac{\partial^2 w}{\partial \xi^2}\)^2d\xi = \frac{1}{2}\b{U}^T_e\left[ \frac{EI}{L^3}\int_0^1\b{B}\b{B}^T d\xi\right] \b{U}_e = \frac{1}{2}\b{U}_e^T K^b_e \b{U}_e](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0049.gif)
但し、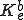 は次のとおり。
は次のとおり。
![K^b_e = \frac{EI}{L^3}\int_0^1\b{B}\b{B}^T d\xi = \frac{EI}{L^3}\[\begin{array}12 & 6L & -12 & 6L \\ 6L & 4L^2 & -6L & 2L^2\\ -12 & -6L & 12 & -6L \\ 6L & 2L^2 & -6L & 4L^2\end{array}\] K^b_e = \frac{EI}{L^3}\int_0^1\b{B}\b{B}^T d\xi = \frac{EI}{L^3}\[\begin{array}12 & 6L & -12 & 6L \\ 6L & 4L^2 & -6L & 2L^2\\ -12 & -6L & 12 & -6L \\ 6L & 2L^2 & -6L & 4L^2\end{array}\]](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0051.gif)
これらを用いると全体の歪みエネルギー は次のように書くことができる。
は次のように書くことができる。
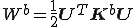
ここで、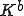 は要素剛性行列
は要素剛性行列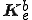 をマージした全体剛性行列であり、
をマージした全体剛性行列であり、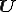 は未知ベクトルである。
は未知ベクトルである。
さて歪みエネルギーの変分を考えて、つりあいの式は次のようになる。
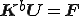
力学的エネルギー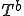 は次のように書くことができる
は次のように書くことができる
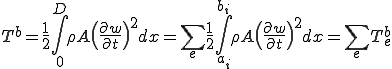
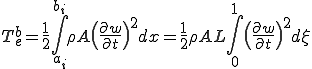
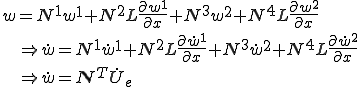
ここで は次のようにおいた
は次のようにおいた
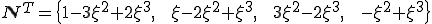
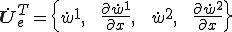
これを用いると運動エネルギーは次のように書くことができる。
![T^b_e = \frac{1}{2}\rho AL\int_0^1 \(\frac{\partial w}{\partial t}\)^2d\xi = \frac{1}{2}\dot{U}^T_e\[\rho AL\int_0^1 N N^T d\xi\]\dot{U}_e = \frac{1}{2}\dot{U}^T_\b{M}_e\dot{U}_e T^b_e = \frac{1}{2}\rho AL\int_0^1 \(\frac{\partial w}{\partial t}\)^2d\xi = \frac{1}{2}\dot{U}^T_e\[\rho AL\int_0^1 N N^T d\xi\]\dot{U}_e = \frac{1}{2}\dot{U}^T_\b{M}_e\dot{U}_e](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0065.gif)
![M_e = \frac{\rho AL}{420}\left[\begin{array} 156 & 22L & 54 & -13L\\ 22L & 4L^2 & 13L & -3L^2\\ 54 & 13L & 156 & -22L\\ -13L & -3L^2 & -22L & 4L^2 \end{array}\right] M_e = \frac{\rho AL}{420}\left[\begin{array} 156 & 22L & 54 & -13L\\ 22L & 4L^2 & 13L & -3L^2\\ 54 & 13L & 156 & -22L\\ -13L & -3L^2 & -22L & 4L^2 \end{array}\right]](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0066.gif)
これらを用いると全体の力学的エネルギー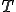 は次のように書くことができる。
は次のように書くことができる。
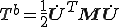
ここで、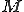 は要素剛性行列
は要素剛性行列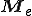 をマージした全体剛性行列であり、
をマージした全体剛性行列であり、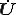 は未知ベクトルの速度である。
は未知ベクトルの速度である。
さて、歪みポテンシャルエネルギー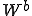 と力学的エネルギー
と力学的エネルギー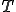 は次のように書けるということになる。
は次のように書けるということになる。

ハミルトンの原理を使うと運動方程式は次のように書ける。
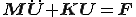
梁曲げの問題では梁の軸方向の歪みも加味して考える。簡単のため、最初にこの梁がx軸に平衡であるとして、x方向の変位に対する剛性行列と質量行列を求める。
軸方向歪みによるエネルギー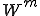 は次のように書ける
は次のように書ける
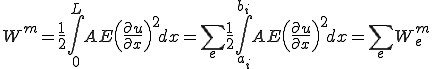
ここで、軸方向変位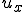 は次のように要素内でアイソパラメトリック補間されるのであった。
は次のように要素内でアイソパラメトリック補間されるのであった。
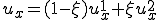
これを用いると軸方向の伸縮による歪みエネルギーは節点変位を使って次のようになる。
![W_e^m = \frac{1}{2}\int_{a_i}^{b_i} AE \left(\frac{\partial u}{\partial x}\right)^2 dx = \frac{1}{2}\int_{0}^{1} AE \left(\frac{u^2_x - u^1_x}{L}\right)^2 Ld\xi = \frac{AE}{2L}(u^1_x - u^2_x)^2\\\;\; = \frac{1}{2}\{\begin{array}u^1_x\\ u^2_x\end{array}\}^T \left[ \frac{AE}{L}\(\begin{array}1 & -1\\ -1 & 1 \end{array}\)\right] \{\begin{array}u^1_x\\ u^2_x\end{array}\} = \frac{1}{2}\{\begin{array}u^1_x\\ u^2_x\end{array}\}^T \b{K}^b_e \{\begin{array}u^1_x\\ u^2_x\end{array}\} W_e^m = \frac{1}{2}\int_{a_i}^{b_i} AE \left(\frac{\partial u}{\partial x}\right)^2 dx = \frac{1}{2}\int_{0}^{1} AE \left(\frac{u^2_x - u^1_x}{L}\right)^2 Ld\xi = \frac{AE}{2L}(u^1_x - u^2_x)^2\\\;\; = \frac{1}{2}\{\begin{array}u^1_x\\ u^2_x\end{array}\}^T \left[ \frac{AE}{L}\(\begin{array}1 & -1\\ -1 & 1 \end{array}\)\right] \{\begin{array}u^1_x\\ u^2_x\end{array}\} = \frac{1}{2}\{\begin{array}u^1_x\\ u^2_x\end{array}\}^T \b{K}^b_e \{\begin{array}u^1_x\\ u^2_x\end{array}\}](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0080.gif)
但し、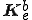 は剛性行列である。
は剛性行列である。
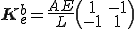
軸方向の変位速度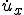 による力学的エネルギー
による力学的エネルギー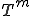 は次のようになる。
は次のようになる。
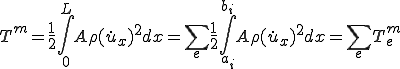
ここで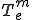 は要素内での力学的エネルギーで、
は要素内での力学的エネルギーで、
![T_e^m = \frac{1}{2}\int_{a_i}^{b_i} A\rho (\dot{u}_x)^2 dx = \frac{1}{2}A\rho L\int^1_0 (\dot{u}_x)^2d\xi\\\;\;\; = \frac{1}{2}A\rho L\int^1_0 \{(1-\xi)\dot{u}^1_x + \xi \dot{u}^2_x\}^2d\xi\\\;\;\; = \frac{1}{2}\{\begin{array}u^1_x\\ u^2_x\end{array}\}^T \left[ A\rho L\(\begin{array}\frac{1}{3} & \frac{1}{6}\\ \frac{1}{3} & \frac{1}{3} \end{array}\)\right] \{\begin{array}u^1_x\\ u^2_x\end{array}\} = \frac{1}{2}\{\begin{array}u^1_x\\ u^2_x\end{array}\}^T \b{M}^b_e \{\begin{array}u^1_x\\ u^2_x\end{array}\} T_e^m = \frac{1}{2}\int_{a_i}^{b_i} A\rho (\dot{u}_x)^2 dx = \frac{1}{2}A\rho L\int^1_0 (\dot{u}_x)^2d\xi\\\;\;\; = \frac{1}{2}A\rho L\int^1_0 \{(1-\xi)\dot{u}^1_x + \xi \dot{u}^2_x\}^2d\xi\\\;\;\; = \frac{1}{2}\{\begin{array}u^1_x\\ u^2_x\end{array}\}^T \left[ A\rho L\(\begin{array}\frac{1}{3} & \frac{1}{6}\\ \frac{1}{3} & \frac{1}{3} \end{array}\)\right] \{\begin{array}u^1_x\\ u^2_x\end{array}\} = \frac{1}{2}\{\begin{array}u^1_x\\ u^2_x\end{array}\}^T \b{M}^b_e \{\begin{array}u^1_x\\ u^2_x\end{array}\}](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0087.gif)
但し、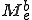 は次のような軸方向変位速度に対する要素質量行列である。
は次のような軸方向変位速度に対する要素質量行列である。
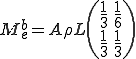
節点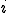 辺りに法線の回転角
辺りに法線の回転角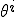 と変位
と変位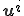 を持つ。
を持つ。
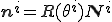
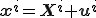
ここで、
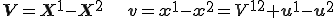
とする。要素の変形前の長さ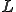 と変形後の長さ
と変形後の長さ は次のとおり
は次のとおり
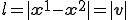
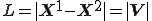
要素内の回転角は、微小かつ要素の長さの変化が小さいと仮定して次のように決める。
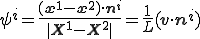
さて、ここで微小歪みを仮定して、要素内の歪みエネルギー が曲げによるエネルギー
が曲げによるエネルギー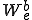 と、軸方向歪みによるエネルギー
と、軸方向歪みによるエネルギー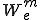 の次のような和であると仮定する。
の次のような和であると仮定する。
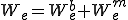
![W^b_e =\frac{1}{2} \{\psi^1, \psi^2\}\frac{2EI}{L^3}\[\begin{array}2 & 1\\ 1 & 2 \end{array}\]\{\begin{array}\psi^1\\ \psi^2\end{array}\} W^b_e =\frac{1}{2} \{\psi^1, \psi^2\}\frac{2EI}{L^3}\[\begin{array}2 & 1\\ 1 & 2 \end{array}\]\{\begin{array}\psi^1\\ \psi^2\end{array}\}](46454D20666F72203244207468696E2D77616C6C6564206265616D_eq0105.gif)
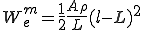
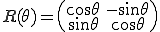
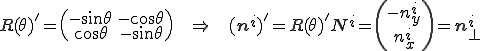
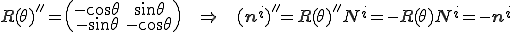
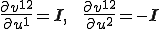
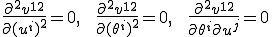
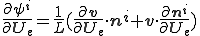
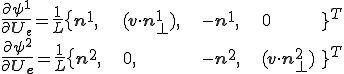
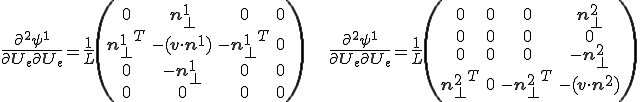
微分の連鎖則から次のように曲げエネルギーの1回微分(=曲げに対する内力)が計算できる。
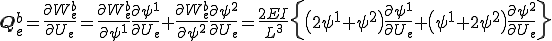

軸方向の歪みエネルギーは次のように、梁の長さの変化で定義した。
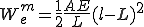
このエネルギーの微分を計算するために、梁の長さを両端のベクトルで微分してみよう。
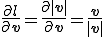
これを用いるとエネルギーの梁の両端を結ぶベクトルでのでの微分は次のとおり。
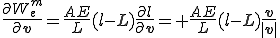
これを用いるとエネルギーの梁の節点変位における微分は次のとおり。
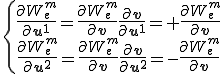
最終的に軸方向の歪みに起因する内力は次のようになる。
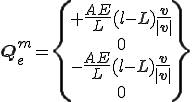
接線剛性行列は歪みエネルギーの2回微分として定義される。
2頂点の長さ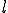 の2頂点を結ぶベクトルで2回微分してみよう。
の2頂点を結ぶベクトルで2回微分してみよう。
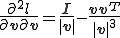
これを用いると軸方向エネルギーの2回微分は次のように書ける。
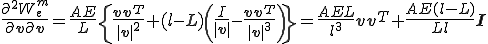
上の第一項が初期変位剛性、第二項は初期応力剛性に対応している。これらを用いて節点変位での微分を計算すると次のようになる。
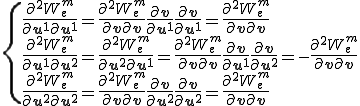
これらを纏めると、軸方向の歪みに起因する接線剛性行列はは以下のとおり。
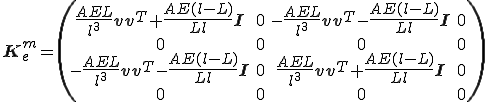
要素内で次のようにエネルギーが定義されていた。
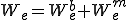
内力と接線剛性行列は、全体のエネルギーの微分であり、エネルギーは要素ごとに曲げと軸方向の歪みを足し合わせて得られた、次のように定義される。
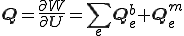
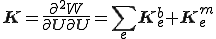
| 非線形有限要素法のためのテンソル解析の基礎 |
久田俊明 著 |
| 連続体力学―簡明な理論と例題 (1979年) (理工学海外名著シリーズ〈31〉) |
P.チャドウィック 著 |
| テンソル解析と連続体力学 (1979年) (理工学海外名著シリーズ〈30〉) |
W.フリューゲ 著 |