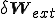 とすると,
とすると,|TOP Page|
圧力剛性とは,非線形有限要素法において,圧力境界条件の変位による厳密な微分によって生じる接線剛性のことである.この接線剛性行列を考慮することで,Newton-Raphson法による増分計算を少ない反復数で収束させる効果がある.
外力による仮想仕事の変分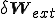 とすると,
とすると,
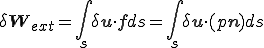
要素 の中で,要素内の節点の番号づけ
の中で,要素内の節点の番号づけ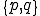 が,グローバルな節点の番号
が,グローバルな節点の番号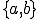 に対応しているとする.
に対応しているとする.
また,形状関数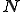 によって,位置
によって,位置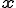 と仮想変位
と仮想変位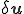 が離散化されているとする.つまり,
が離散化されているとする.つまり,
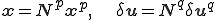
であるとする.このとき,仮想変位によるエネルギーの変分を次のように表すことができる.
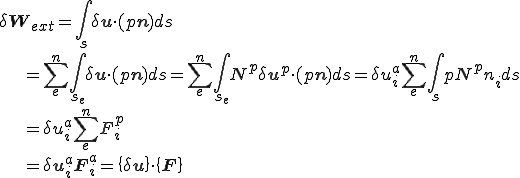
ここで,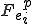 は要素内節点等価外力ベクトルであり,
は要素内節点等価外力ベクトルであり,
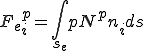
である.この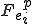 を具体的に各要素について計算してみよう.
を具体的に各要素について計算してみよう.
アイソパラメトリック要素の場合は次のように単位法線ベクトルが表される.
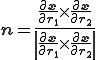
また微小面積は次のようになる.
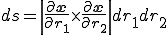
これを用いると要素内等価節点外力は次のとおり.
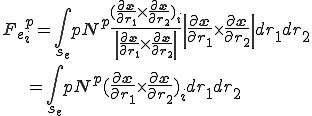
具体的にアイソパラメトリック要素の形状が四角形の場合と三角形の場合でこれを計算してみよう.
![r_1=[-1,1],\;\;r_2=[-1,1] r_1=[-1,1],\;\;r_2=[-1,1]](50726573737572652053746966666E657373_eq0017.gif)
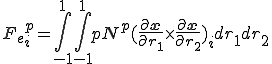
![r_1=[0,1-r_2],\;\;r_2=[0,1] r_1=[0,1-r_2],\;\;r_2=[0,1]](50726573737572652053746966666E657373_eq0019.gif)
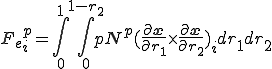
三角形一次要素の場合は,法線が面内で一定である.
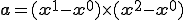
とおくと,面積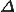 は
は
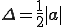
と書ける.また,面の単位法線ベクトル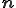 は
は
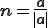
となる.これらを用いると
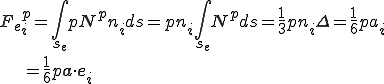
となる.
圧力剛性行列(pressuer stiffness matrix)は圧力による等価節点外力の節点変位による微分で計算できる.
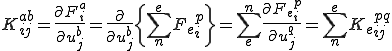
となる.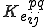 は要素剛性行列で,
は要素剛性行列で,
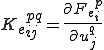
である.これを具体的に計算すると以下のようになる.
圧力はUpdate Lagrange的に取り扱う.
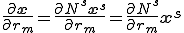
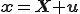
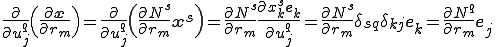
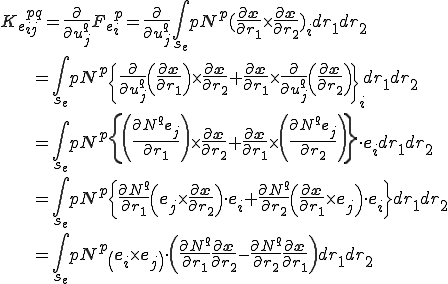
座標の添え字に対して反対称(Skew Symmetric)
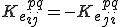
であることがわかる.
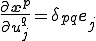
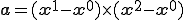
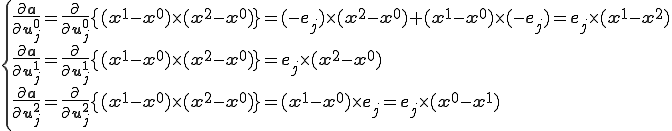
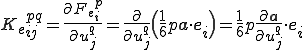
これを用いると,
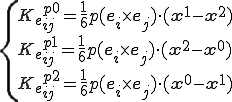
となる.こちらも座標の添え字に対して反対称(Skew Symmetric)
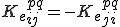
であることがわかる.
| 非線形有限要素法のためのテンソル解析の基礎 | 久田俊明 著 |