|TOP Page|
ポアソン方程式(Poisson's Equation)を解く問題を次のように定義する。
| 問題設定 |
|---|
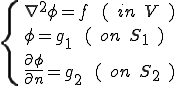 |
境界条件は値が決定されている場合のDirichlet条件と,法線方向の微分値が決定されている場合のNeumann条件の2種類に分けられる.これらは,第一種境界条件,第二種境界条件または,基本境界条件,自然境界条件と呼ばれる場合もある.境界はDirichlet条件かNeumann条件のどちらかが設定されていなくては,解が定まらない.また,Dirichlet条件とNeumann条件が与えられる境界は重複してはならない.つまり,
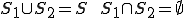
以下強形式で書かれたポアソン方程式を弱形式に変形する.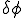 を
を
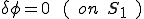
を満たす任意の関数とする.上式に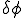 をかけて,
をかけて, 上で積分すると
上で積分すると
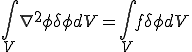
となる. ここで,微分の連鎖則より
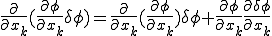
が成り立つ.これを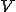 内で積分すると
内で積分すると
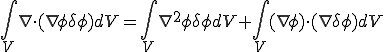
第2項に前式を代入する.また,右辺と左辺を入れ替えると,
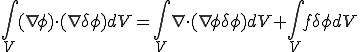
右辺第一項について考える。この項にGaussの発散定理を用いると
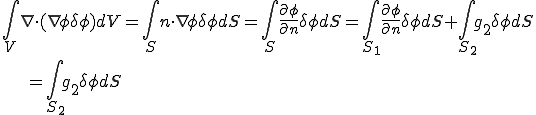
となる。ここで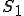 上では
上では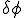 は0であることを用いた
は0であることを用いた
これを上式に代入すると弱形式で書かれたポアソン方程式は以下の通りになる。
| 弱形式ポアソン方程式 |
|---|
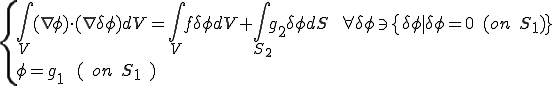 |
弱形式で書かれたラプラス方程式は以下の通り
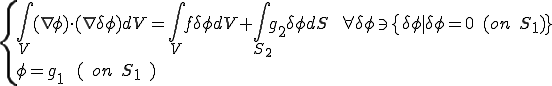
上式を成分で書くと
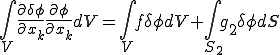
のようになる。ここでは について総和規約を適応している。上式は積分で書かれている。積分とはつまり和であるので積分領域を分割してた中で積分を実行し、それを足し合わせて上式を計算してもよい。
について総和規約を適応している。上式は積分で書かれている。積分とはつまり和であるので積分領域を分割してた中で積分を実行し、それを足し合わせて上式を計算してもよい。
そこで を要素分割した領域を
を要素分割した領域を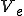 、
、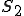 を要素分割した領域を
を要素分割した領域を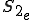 とすると定式は次のように書ける。
とすると定式は次のように書ける。
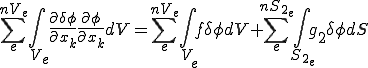
但し、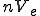 、
、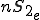 はそれぞれ
はそれぞれ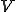 と
と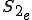 の要素分割数である。
の要素分割数である。
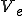 内で関数
内で関数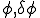 は次のような形状関数
は次のような形状関数 によって離散化されているとする。
によって離散化されているとする。
但し、固定境界条件が設定されている面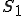 上の節点
上の節点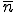 では
では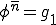 、
、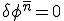 である。
である。
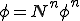 、
、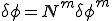
同様に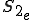 内で関数
内で関数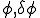 は次のような形状関数
は次のような形状関数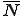 によって離散化されているとする。
によって離散化されているとする。
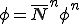 、
、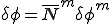
形状関数で補間された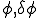 を上式に代入して
を上式に代入して
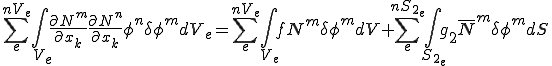
ここで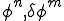 は節点の値であり,関数ではないので積分の外に出すことができる。それぞれ積分の外に出した後にまとめると次のようになる。
は節点の値であり,関数ではないので積分の外に出すことができる。それぞれ積分の外に出した後にまとめると次のようになる。
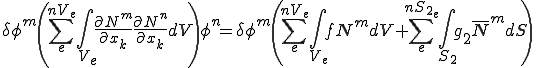
次のように行列表記できる。
| 離散化されたポアソン方程式 |
|---|
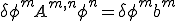 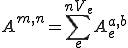 (但し、要素内節点番号a,bは全体節点番号m,n) |
| 要素剛性行列 |
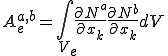 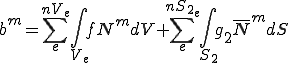 |
上式をマトリックス表記すると次のようになる。
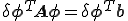
このままでは連立一次方程式として解くことができない。
固定境界条件が設定されている面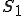 上の節点
上の節点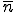 では
では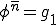 、
、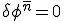 はGivenであった。面
はGivenであった。面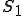 上の
上の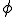 の値を
の値を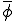 とする。また、未知数のある面
とする。また、未知数のある面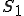 上以外の点における
上以外の点における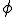 ,
,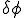 の値を
の値を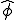 ,
,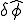 とすると上の方程式は次のようになる。
とすると上の方程式は次のようになる。
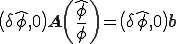
これは展開して次のように書くことができる。
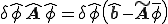
但し、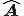 は未知自由度について
は未知自由度について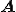 の成分を取り出してきた行列である。また
の成分を取り出してきた行列である。また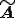 は行が未知自由度、列が既知自由度である
は行が未知自由度、列が既知自由度である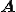 の成分を取り出してきた行列である、さらに
の成分を取り出してきた行列である、さらに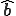 は未知自由度について
は未知自由度について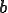 の成分を取り出してきたベクトルである。
の成分を取り出してきたベクトルである。
ここで任意の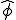 の値について上式が成り立たなければいけなかったことに注意して
の値について上式が成り立たなければいけなかったことに注意して
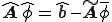
のように書ける。この形にすることによって、計算して解を求めることが可能である。
残差と増分について解くとより簡単な式が得られる。上式を増分について解いてみる。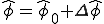 を代入すると
を代入すると
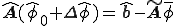
これを変形すると、
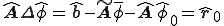
ただし、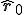 は残差
は残差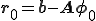 の未知自由度のみを取り出したものである。
の未知自由度のみを取り出したものである。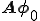 を計算することは、
を計算することは、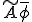 を計算するよりも計算負荷が大きくなる可能性がある。しかし、非線形方程式を解く場合は通常残差と増分に対して解くので残差はどのみち計算しなければならず余分な手間とはならない。非線形方程式を解く場合はこの種類の境界条件処理をよく使う。
を計算するよりも計算負荷が大きくなる可能性がある。しかし、非線形方程式を解く場合は通常残差と増分に対して解くので残差はどのみち計算しなければならず余分な手間とはならない。非線形方程式を解く場合はこの種類の境界条件処理をよく使う。
単純な形状の場合は数値積分を用いなくても解析的に積分を実行することができる.この場合について,簡単に纏めておく.
三角形や四面体の一次の内挿関数は線形である。節点 に対する内挿関数を
に対する内挿関数を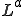 のように書く。
のように書く。
線形であるので空間微分は定数。つまり要素内で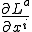 は一定である。これから剛性行列を求める際の被積分も定数となるので、この定数に要素の面積や体積を掛けることで積分を実行することができる。これ用いると次のように要素剛性行列を書くことができる。
は一定である。これから剛性行列を求める際の被積分も定数となるので、この定数に要素の面積や体積を掛けることで積分を実行することができる。これ用いると次のように要素剛性行列を書くことができる。
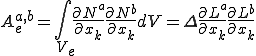
但し、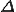 は2次元の場合は三角形の面積、3次元の場合は四面体の体積である。
は2次元の場合は三角形の面積、3次元の場合は四面体の体積である。
ここで、
area=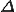 、dldx[a][i] =
、dldx[a][i] = 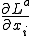
emat[a][b] = 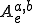
のように変数が対応している場合、プログラムの例は次のとおり
// 要素剛性行列を求める
for(unsigned int inoel=0;inoel<nnoel;inoel++){
for(unsigned int jnoel=0;jnoel<nnoel;jnoel++){
double dtmp1 = 0.0;
for(unsigned int idim=0;idim<ndim;idim++){
dtmp1 += dldx[inoel][idim]*dldx[jnoel][idim];
}
emat[inoel][jnoel] = area*dtmp1;
}
}
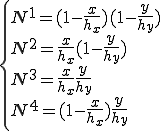
これらのx微分、y微分を計算すると、
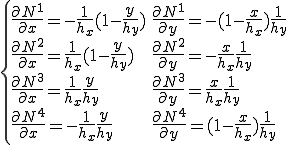
積分を行うと次のとおり、
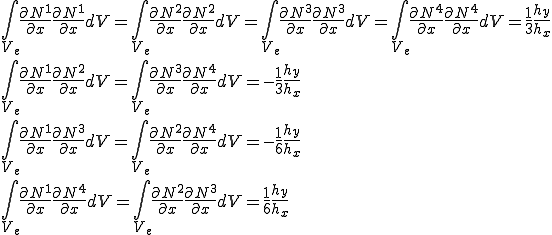
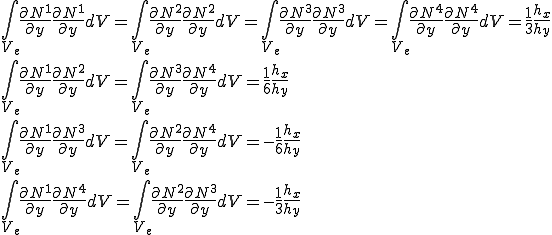
よって、要素剛性行列は次のとおり
![A^{a,b}=\int_V_e\frac{\partial N^a}{\partial x}\frac{\partial N^b}{\partial x}+\frac{\partial N^a}{\partial y}\frac{\partial N^b}{\partial y}dV =\frac{1}{6h_yh_x}\[\begin{array}{llll} 2(h_y^2+h_x^2) & -2h_y^2+h_x^2& -h_y^2-h_x^2 & h_y^2-2h_x^2\\ -2h_y^2+h_x^2 & 2(h_y^2+h_x^2) & h_y^2-2h_x^2 & -h_y^2-h_x^2\\ -h_y^2-h_x^2 & h_y^2-2h_x^2 & 2(h_y^2+h_x^2) & -2h_y^2+h_x^2\\ h_y^2-2h_x^2 & -h_y^2-h_x^2 & -2h_y^2+h_x^2 & 2(h_y^2+h_x^2)\end{array}\] A^{a,b}=\int_V_e\frac{\partial N^a}{\partial x}\frac{\partial N^b}{\partial x}+\frac{\partial N^a}{\partial y}\frac{\partial N^b}{\partial y}dV =\frac{1}{6h_yh_x}\[\begin{array}{llll} 2(h_y^2+h_x^2) & -2h_y^2+h_x^2& -h_y^2-h_x^2 & h_y^2-2h_x^2\\ -2h_y^2+h_x^2 & 2(h_y^2+h_x^2) & h_y^2-2h_x^2 & -h_y^2-h_x^2\\ -h_y^2-h_x^2 & h_y^2-2h_x^2 & 2(h_y^2+h_x^2) & -2h_y^2+h_x^2\\ h_y^2-2h_x^2 & -h_y^2-h_x^2 & -2h_y^2+h_x^2 & 2(h_y^2+h_x^2)\end{array}\]](46454D20666F7220506F6973736F6E2773204571756174696F6E_eq0092.gif)
ここで、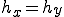 の時は特別に次のようになる。
の時は特別に次のようになる。
![A^{a,b}=\[\begin{array}{cccc}\frac{2}{3}&-\frac{1}{6}&-\frac{1}{3}&-\frac{1}{6}\\ -\frac{1}{6}&\frac{2}{3}&-\frac{1}{6}&-\frac{1}{3}\\ -\frac{1}{3}&-\frac{1}{6}&\frac{2}{3}&-\frac{1}{6}\\ -\frac{1}{6}&-\frac{1}{3}&-\frac{1}{6}&\frac{2}{3}\\ \end{array}\] A^{a,b}=\[\begin{array}{cccc}\frac{2}{3}&-\frac{1}{6}&-\frac{1}{3}&-\frac{1}{6}\\ -\frac{1}{6}&\frac{2}{3}&-\frac{1}{6}&-\frac{1}{3}\\ -\frac{1}{3}&-\frac{1}{6}&\frac{2}{3}&-\frac{1}{6}\\ -\frac{1}{6}&-\frac{1}{3}&-\frac{1}{6}&\frac{2}{3}\\ \end{array}\]](46454D20666F7220506F6973736F6E2773204571756174696F6E_eq0094.gif)
各点におけるステンシルは次のとおり
![\frac{1}{3}\[\begin{array}{ccc}-1&-1&-1\\-1&8&-1\\-1&-1&-1\end{array}\] \frac{1}{3}\[\begin{array}{ccc}-1&-1&-1\\-1&8&-1\\-1&-1&-1\end{array}\]](46454D20666F7220506F6973736F6E2773204571756174696F6E_eq0095.gif)
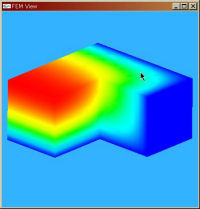
次のサンプルプログラムは大きさ1×1の矩形領域における次のようなポアソン方程式(Poisson's Equation)を解く問題である。
プログラムを実行すると'solution.dat'という結果ファイルが生成される。
'solution.dat'はgnuplot用のデータ形式をしている
windows版のgnuplotの導入は以下のページが詳しい
gnuplotを起動した後、プログラムを実行した'solution.dat'のあるディレクトリに移動し、次のようなコマンドを打つと結果が表示される。
gnuplot> set style data line gnuplot> splot 'solution.dat'
軸対称な問題を考えてみよう.つまり解析領域や境界条件や物性に周方向の変化が無い場合を考える.この場合解も軸対称と考えられ,厚さ方向の変化を無視した場合と同様に3次元の問題を2次元的に取り扱うことができる.
円柱座標系を考えた場合,対象となる場は軸までの距離とz座標の変数として表される.ここでは簡単のため,回転軸がz軸と一致していると考える.この時,場は次のように表される.
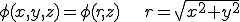
これらの微分を計算すると以下のとおりになる.
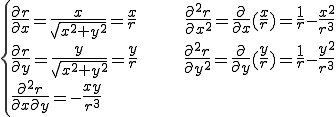
これらを用いて
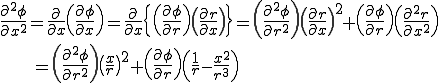
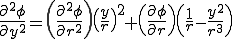
これらを用いて直交座標におけるラプラス演算子を計算すると以下のとおりになる.
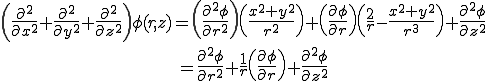
よって,軸対称問題の円筒座標系におけるラプラス方程式は次のように書ける
| 軸対称問題の円筒座標系におけるラプラス方程式 |
|---|
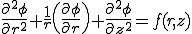 |
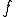 は単位体積あたりのソースを表している.この
は単位体積あたりのソースを表している.この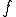 も軸対称であることに注意されたい.
も軸対称であることに注意されたい.
軸対称に固定境界条件とし自然境界条件が定義されているとする.
固定境界上で0となる,軸対称な関数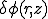 を上式に掛け,領域全体で積分する.
を上式に掛け,領域全体で積分する.
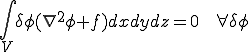
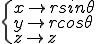
この場合のヤコビアンの絶対値は
![\det J(r,\theta,z)=\det \[\begin{array} \sin\theta & r \cos\theta & 0 \\ \cos\theta & -r\sin\theta & 0 \\ 0 & 0 & 1 \end{array}\] = r \det J(r,\theta,z)=\det \[\begin{array} \sin\theta & r \cos\theta & 0 \\ \cos\theta & -r\sin\theta & 0 \\ 0 & 0 & 1 \end{array}\] = r](46454D20666F7220506F6973736F6E2773204571756174696F6E_eq0109.gif)
となるので,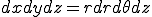 となる.これを上に代入すると,
となる.これを上に代入すると,
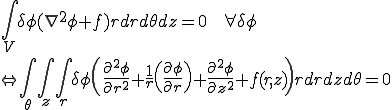
ここで,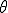 方向の変化が無いことを考慮して,
方向の変化が無いことを考慮して,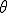 の積分を除外できる.これをガウスの発散定理を用いて弱形式に変換する
の積分を除外できる.これをガウスの発散定理を用いて弱形式に変換する
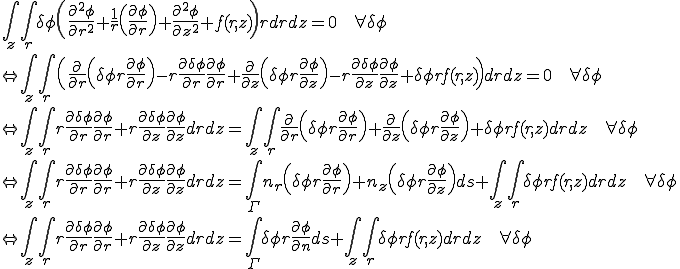
断面の2次元的な領域を ,
, とすると次のようになる.
とすると次のようになる.
| 弱形式化された円柱座標でのラプラス方程式 |
|---|
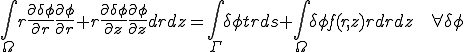 |
上の弱形式化では軸対称な問題を断面の2次元問題に帰着させた.さて断面の領域がメッシュ分割されているとしてみよう.積分は積分領域を要素単位で分けて足し合わせて計算するとして上の式は以下のようになる.
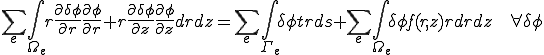
ガラーキン法を用いた離散化をするとして,要素の中で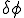 と
と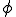 が2次元の断面上で補間関数
が2次元の断面上で補間関数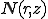 を使って次のように要素分割されているとする.
を使って次のように要素分割されているとする.
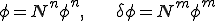
要素の中での番号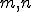 は全体での番号
は全体での番号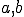 に対応しているとする.また,自然境界条件が課されている表面の要素は形状関数
に対応しているとする.また,自然境界条件が課されている表面の要素は形状関数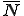 で離散化されているとする.これを上に代入すると以下のようになる.
で離散化されているとする.これを上に代入すると以下のようになる.
![\sum\int_{\Omega_e} r\frac{\partial N^m\delta\phi^m}{\partial r}\frac{\partial N^n\phi^n}{\partial r} + r\frac{\partial N^m\delta\phi^m}{\partial z}\frac{\partial N^n\phi^n}{\partial z} drdz = \sum_e\int_{\Gamma_e} \bar{N}^m\delta\phi^m trds + \sum_e\int_{\Omega_e} N^m\delta\phi^m f(r,z) rdrdz\;\;\forall \delta\phi\\ \Leftright \sum_e\[\delta\phi^m\int_\Omega r\frac{\partial N^m}{\partial r}\frac{\partial N^n}{\partial r} + r\frac{\partial N^m}{\partial z}\frac{\partial N^n}{\partial z} drdz\phi^n \] = \sum_e\[\delta\phi^m \int_{\Gamma_e} \bar{N}^mtrds\] + \sum_e\[\delta\phi^m\int_{\Omega_e} N^m f(r,z) rdrdz\]\;\;\forall \delta\phi\\ \Leftright \sum_e\[\delta\phi^m A_e^{mn}\phi^n \] = \sum_e\[\delta\phi^m {f_e}_{out}^m\] + \sum_e\[\delta\phi^mf_e_{in}^m\]\;\;\forall \delta\phi\\ \Leftright \delta\phi^a\[ \sum_e A_e^{mn} \]\phi^b = \delta\phi^a\[ \sum_e {f_e}_{out}^m\] + \delta\phi^a\[ \sum_e {f_e}_{in}^m\]\;\;\forall \delta\phi\\ \Leftright \delta\phi^aA^{ab}\phi^b = \delta\phi^a f_{out}^a + \delta\phi^a f_{in}^a\;\;\forall \delta\phi \sum\int_{\Omega_e} r\frac{\partial N^m\delta\phi^m}{\partial r}\frac{\partial N^n\phi^n}{\partial r} + r\frac{\partial N^m\delta\phi^m}{\partial z}\frac{\partial N^n\phi^n}{\partial z} drdz = \sum_e\int_{\Gamma_e} \bar{N}^m\delta\phi^m trds + \sum_e\int_{\Omega_e} N^m\delta\phi^m f(r,z) rdrdz\;\;\forall \delta\phi\\ \Leftright \sum_e\[\delta\phi^m\int_\Omega r\frac{\partial N^m}{\partial r}\frac{\partial N^n}{\partial r} + r\frac{\partial N^m}{\partial z}\frac{\partial N^n}{\partial z} drdz\phi^n \] = \sum_e\[\delta\phi^m \int_{\Gamma_e} \bar{N}^mtrds\] + \sum_e\[\delta\phi^m\int_{\Omega_e} N^m f(r,z) rdrdz\]\;\;\forall \delta\phi\\ \Leftright \sum_e\[\delta\phi^m A_e^{mn}\phi^n \] = \sum_e\[\delta\phi^m {f_e}_{out}^m\] + \sum_e\[\delta\phi^mf_e_{in}^m\]\;\;\forall \delta\phi\\ \Leftright \delta\phi^a\[ \sum_e A_e^{mn} \]\phi^b = \delta\phi^a\[ \sum_e {f_e}_{out}^m\] + \delta\phi^a\[ \sum_e {f_e}_{in}^m\]\;\;\forall \delta\phi\\ \Leftright \delta\phi^aA^{ab}\phi^b = \delta\phi^a f_{out}^a + \delta\phi^a f_{in}^a\;\;\forall \delta\phi](46454D20666F7220506F6973736F6E2773204571756174696F6E_eq0126.gif)
但し,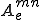 は要素剛性行列で,
は要素剛性行列で,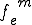 は外力ベクトルであり,次のように書くことができる.
は外力ベクトルであり,次のように書くことができる.
| 要素剛性行列 |
|---|
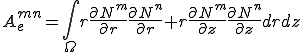 |
| 外力ベクトル |
|---|
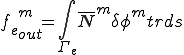 |
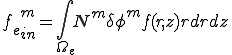 |
三角形一次要素のような単純な場合は解析的に要素剛性行列の積分を行うことができる.このような一次要素による線形な補間関数を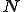 の変わりに
の変わりに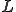 を使って表す.
を使って表す.
軸までの距離 も三角形内で一次的に変化するから
も三角形内で一次的に変化するから
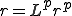
というように,節点の値の補間によって得ることができる.
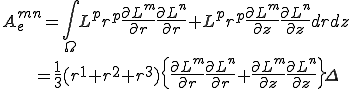
但し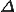 は三角形の面積である.結局この場合,重心位置での距離に2次元三角形のラプラス方程式の要素剛性を掛けたものになることが分かる.
は三角形の面積である.結局この場合,重心位置での距離に2次元三角形のラプラス方程式の要素剛性を掛けたものになることが分かる.
| 有限要素法概説―理工学における基礎と応用 (FEM+BEM (3)) |
菊池文雄 著 |
| 流れと熱伝導の有限要素法入門 | 矢川元基 著 |