MPC with Lagrange Multiplier

ラグランジュ未定乗数による多点拘束問題

Last Update:2009年05月15日

概要

有限要素法において複数の節点が自由な値を取ることができずに，まとめて何らかの制約を受けるような場合を考えよう．これは一般的に多点拘束,ＭＰＣ(Multiple Point Constraint)と呼ばれる．ここではラグランジュ未定乗数法を用いたMPCについて説明する．

拘束条件の取り扱い方の分類

このような拘束条件が付加される場合には以下の３つのやり方が考えられる．

自由度の削減
ペナルティ法
ラグランジュ未定乗数法

自由度の削減は，例えば固体の解析なら変位のxy方向拘束をする場合にx節点の自由度を削減して連立一次方程式を立てることに相当する．ペナルティ法は制約条件から離れてしまうと大きな力が発生するような硬いバネを入れて解く方法である．ラグランジュ未定乗数法は拘束力を未知数として一緒に解く方法である．自由度を削減するやり方は自由度が減りロバストなものの，使える機会が限られる．ペナルティ法は自由度の数はそのままでコーディングも楽だが反復法で連立一次方程式が解きづらくなる．また人工的なパラメータ(硬いバネのバネ定数)が必要であるし，厳密には拘束条件を満たさない．ラグランジュ未定乗数法は自由度が拘束力の分だけ増えるものの，大抵の拘束条件に応用できるので汎用性がある．行列が不定値になり，反復解法でやや解きづらくなるが，ペナルティイ法ほど重大ではない．

ラグランジュ未定乗数法

変位 $\b{u}$ に対する制約条件が $G(\b{u})=0$ という風に書けるとすると，このような問題は

$\min\; W(\b{u})\;\; while\; G(\b{u})=0$

というようにかける．

制約条件下での変分法

上の制約条件を満たす範囲内での極値問題をそのまま変分的に書くと，解は次を満たす．

$\{\begin{array}{l}\delta W = \frac{\partial W}{\partial \b{u}}\cdot\delta\b{u}_{\parallel} = 0\;\;\forall\delta\b{u}_{\parallel}\in \cal{T}\\ G(\b{u})=0 \end{array}$

但し $\cal{T}$ は $\b{u}$ におけるの接空間である．

つまり $\delta\b{u}_{\parallel}\in\cal{T}$ は $\frac{\partial G}{\partial\b{u}}\cdot \delta\b{u}_{\parallel}=0$ を $\b{u}$ において満たす

ラグランジュ未定乗数を用いた変分法

上の定式化では，の接部分空間 $\delta\b{u}_{\parallel}$ を考えなければいけなく，有限要素法では一般的に取り扱いが困難である．そこでこのような空間を考えなくてもよい方法がラグランジュ未定乗数を使った方法である．

上式から，解の周辺においてとの接空間が一致することがわかる．よって，

$\frac{\partial W}{\partial\b{u}}$ と $\frac{\partial G}{\partial\b{u}}$ が平行になる．

つまり，あるスカラー量 $\lambda$ を使って，

$\frac{\partial W}{\partial\b{u}}=-\lambda\frac{\partial G}{\partial\b{u}}$

と書くことができる．この $\lambda$ がラグランジュ未定乗数である．以上からこの問題の解は

$W'(\b{u})=W(\b{u})+\lambda G(\b{u})$

の極値となることがわかる．つまり，

$\delta W' = \frac{\partial W}{\partial\b{u}}\cdot\delta\b{u} + \lambda\frac{\partial G}{\partial\b{u}}\cdot\delta\b{u} + G(\b{u})\delta\lambda \\\;\; = (\frac{\partial W}{\partial\b{u}}+\lambda\frac{\partial G}{\partial\b{u}})\cdot\delta\b{u} + G(\b{u})\delta\lambda$

を解は満たすことがわかる．

未定乗数の意味

関数の選び方は幾つも考えられるが

$|\frac{\partial G}{\partial \b{u}}| = 1$

を満たすようにしておくと，

$\frac{\partial W}{\partial \b{u}}+\lambda\frac{\partial G}{\partial\b{u}}=0$

$|\frac{\partial W}{\partial\b{u}}|=|\lambda||\frac{\partial G}{\partial \b{u}}|=\lambda$

であるから， $\lambda$ は制約条件の満たされない方向へのエネルギーの勾配の大きさに等しくなる．エネルギーの変位での微分は力であるから，この場合 $\lambda$ は拘束力の大きさを意味している．このようにLagrange未定乗数に拘束力の大きさとしての意味づけをすることができるので便利である．

複数の拘束条件

拘束条件が複数ある場合を考える

$\min\; W(\b{u})\;while\;G^k(\b{u})=0\;\{k=1,\ldots,n\}$

この場合,極値が満たす条件は以下のとおり．

$\{\begin{array}{l}\delta W = \frac{\partial W}{\partial \b{u}}\cdot\delta\b{u}_{\parallel} = 0\;\;\forall\delta\b{u}_{\parallel}\in\cal{T}\\ G^k(\b{u})=0\;\;\{k=1,\ldots,n\} \end{array}$

但し， $\cal{T}$ は $G^k\;\{k=1,\ldots,n\}$ の接空間の積集合である．

つまり， $\delta\b{u}_{\parallel}\in\cal{T}$ に対して， $\frac{\partial G^k}{\partial u}\cdot\delta\b{u}_{\parallel} = 0\;\;\{k=1,\ldots,n\}$ となる．

において，の接空間と $G^k\;\{k=1,\ldots,n\}$ の接空間の積集合は一致している．よって，それぞれの補空間や直交補空間は一致しているはずである(これは接空間が閉空間である場合にのみ言えることで，非圧縮性拘束条件などの場合は補間方法によっては成り立たない場合がある)．直交補空間は補空間に含まれる． $\frac{\partial W}{\partial u}$ は直交補空間で， $\frac{\partial G^k}{\partial u}\;\{k=1,\ldots,n\}$ の和集合は補空間である．

$\frac{\partial W}{\partial u} \in span\{\frac{\partial G^1}{\partial u},\frac{\partial G^2}{\partial u},\ldots,\frac{\partial G^n}{\partial u}\}$

よって，ある実数 $\lambda^k$ が存在して，

$\frac{\partial W}{\partial u}=\sum_k^n\lambda^k\frac{\partial G^k}{\partial u}$

となる．これは次のポテンシャルエネルギーの極値となる．

$W'(\b{u})=W(\b{u})+\sum_k^n\lambda^k G^k(\b{u})$

有限要素法における定式化

有限要素法のラグランジュ未定乗数の例として，各節点ごとにベクトル値を持っていて，全体のポテンシャルエネルギーが節点のベクトル値の関数で表されていて，制約条件も各節点のベクトル値について個別に付加される状況を考える．

$\min\;W(\b{u})\;while\;G(\b{u}^k)=0\;(k=1,\ldots,#constrain)$

このときの制約条件化でのポテンシャルエネルギーの仮想変分を考えてみよう．制約条件が課されている節点について変分をとる．制約条件が課されていなければ取り扱いは同じである．

$\delta W' = \frac{\partial W}{\partial\b{u}^a_i}\delta\b{u}^a_i + \lambda^a\frac{\partial G}{\partial\b{u^a}^a_i}\delta\b{u}^a_i + G(\b{u})\delta\lambda^a \\\;\;\;\; = (\frac{\partial W}{\partial\b{u}^a_i}+\lambda^a\frac{\partial G}{\partial\b{u}^a_i})\delta\b{u}^a_i + G(\b{u})\delta\lambda^a\\\;\;\;\; = \{Q_u\}^a_i\delta\b{u}^a_i + \{Q_\lambda\}^a\delta\lambda^a$

ここで， $\{Q_u\},\{Q_\lambda\}$ はそれぞれ，変位と拘束力についての等価節点内力で次の通りである．

$\{\begin{array}{l}\{Q_u\}^a_i=\frac{\partial W}{\partial\b{u}^a_i}+\lambda^a\frac{\partial G}{\partial\b{u}^a_i}\\\{Q_\lambda\}^a=G(\b{u}^a)\end{array}$

これを微分することで接線剛性行列を考えてみよう

$\{\begin{array}{l}[K_{uu}]^{ab}_{ij}=\frac{\partial \{Q_u\}^a_i}{\partial {u}^b_j} = \frac{\partial^2 W}{\partial\b{u}^a_i\partial\b{u}^b_j}+\lambda^a\frac{\partial^2 G}{\partial\b{u}^a_i\partial\b{u}^b_j}\delta_{ab}\\ [K_{u\lambda}]^{ab}_{i}=\frac{\partial \{Q_u\}^a_i}{\partial {\lambda}^b} = \frac{\partial G}{\partial\b{u}^a_i}\delta_{ab}\\ [K_{\lambda u}]^{ab}_{\;j}=\frac{\partial \{Q_\lambda\}^a}{\partial u^b_j } = \frac{\partial G}{\partial\b{u}^b_j}\delta_{ab}\\ [K_{\lambda \lambda}]^{ab}=\frac{\partial \{Q_\lambda\}^a}{\partial \lambda^b } = 0 \end{array}$

係数行列は対称となるこことがわかる．最終的に次の連立一次方程式を解くことで解が得られる

$\[\begin{array}{ll}[K_{uu}]^{ab}_{ij}&[K_{u\lambda}]^{ab}_{i}\\[K_{\lambda u}]^{ab}_{\;j}&[K_{\lambda\lambda}]^{ab} \end{array}\] \{\begin{array}\{u\}^b_j\\\{\lambda\}^b\end{array}\} = \{\begin{array}\{f\}^b_j\\0\end{array}\} - \{\begin{array}\{Q_u\}^b_j\\\{Q_\lambda\}^b\end{array}\}$

節点が直線上にあるという拘束

固体の解析にこのラグランジュ未定乗数による拘束を適応してみよう．

節点が直線上にあるという拘束を考える．例えば点 $\b{p}$ を通り，単位法線ベクトルが $\b{n}$ である直線より上にあるという条件は

$G(\b{u})=(\b{x}-\b{p})\cdot\b{n}\\\;\;\;\; = (\b{X}+\b{u}-\b{p})\cdot\b{n} = 0$

と書ける．但し節点の変形後の位置が $\b{x}$ で変位が $\b{u}$ で，変形前の位置が $\b{X}$ である．

$\frac{\partial G(\b{u})}{\partial u_i} = n_i$

であるから，

$\{\begin{array}{l}[K_{uu}]^{ab}_{ij}=\frac{\partial^2 W}{\partial\b{u}^a_i\partial\b{u}^b_j}\\ [K_{u\lambda}]^{ab}_{i}=n_i\delta_{ab}\\ [K_{\lambda u}]^{ab}_{\;j}=n_j\delta_{ab}\\ [K_{\lambda \lambda}]^{ab}=0 \end{array}$

のようになる． $[K_{uu}]^{ab}_{ij}$ は拘束なしの剛性行列と同一である．

動画による解析例の紹介

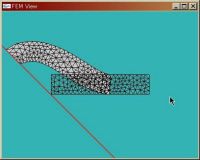
下の動画はラグランジュ未定乗数法を用いて，梁の左端の節点が赤い直線の上に来るように制約条件を付け加えた物．梁は線形弾性体を使い，右端には正弦波状の変位を与えている．

剛体への節点の張り付つけ

２次元問題

制約条件の定式化

変形前の状態において，剛体の一点(普通は重心)が $\b{p}$ として，そこから $\b{b}$ だけ離れた点 $\b{X}=\b{p}+\b{b}$ に節点が固定されているとする.この場合に剛体上に節点が貼り付けられているとしよう．剛体の一点の変位がとして，剛体のこの点周りの回転が $\Theta$ と表されるとする．このとき剛体に貼り付けられた節点の位置 $\b{x}$ は次のようになる．

$\b{x}=\b{p}+\b{U}+R(\Theta)\b{b} = \b{X}-\b{b}+\b{U}+R(\Theta)\b{b}$

ここで， $R(\Theta)$ は回転を表し，

$R(\Theta)\b{b} = cos\Theta\b{b}+sin\Theta(\b{z}\times\b{b})$

である．また， $\Theta$ による１回微分，２回微分は

$\frac{\partial R(\Theta)\b{b}}{\partial \Theta} = -sin\Theta\b{b}+cos\Theta(\b{z}\times\b{b}) = \b{z}\times \{R(\Theta)\b{b}\}$

$\frac{\partial^2 R(\Theta)\b{b}}{\partial^2 \Theta} = \b{z}\times\frac{\partial R(\Theta)\b{b}}{\partial \Theta} = \b{z}\times\[\b{z}\times \{R(\Theta)\b{b}\}\] = - R(\Theta)\b{b}$

のようになる．

ここで，節点変位 $\b{u}=\b{x}-\b{X}$ は次のようになる．

$\b{u}=\b{U}+(R(\Theta)-I)\b{b}$

これは成分で書くと

$\b{u}_i=\b{U}_i+\{(R(\Theta)-I)\b{b}\}_i$

最終的に拘束条件は，

$G(\b{u}_i)=\b{u}_i-\b{U}_i-\{(R(\Theta)-I)\b{b}\}_i$

ポテンシャルの修正

となる．節点の座標を所定の位置に完全に固定してしまうので，ラグランジュ未定乗数はxy成分に必要である．さて，歪エネルギーポテンシャル関数をとして，この拘束条件を考慮した新たなポテンシャルは次のとおりになる．

$W'=W+\sum_k^n\lambda^{a(k)}_i\[u^{a(k)}_i-U_i-\{(R(\Theta)-I)\b{b}^{a(k)}\}_i\]\;(k=1,\ldots,#constrain)$

但し， a(k) は番目の制約条件の節点番号を表す．

節点等価内力の計算

このときの制約条件化でのポテンシャルエネルギーの仮想変分を考えてみよう．制約条件が課されている節点について変分をとる．制約条件が課されていない節点は制約条件が無い場合と取り扱いは同じである．

$\delta W' = \frac{\partial W}{\partial u^a_i}\delta u^a_i+\delta\lambda^a_i\[u^a_i-U_i-\{(R(\Theta)-I)\b{b}^a\}_i\]+\lambda^a_i\[\delta u^a_i-\delta U_i-\{\frac{\partial R(\Theta)\b{b}^a}{\partial \Theta}\}_i\delta\Theta\]\\\;\;\; = $\frac{\partial W}{\partial u^a_i}+\lambda^a_i$\delta u^a_i + \[u^a_i-U_i-\{(R(\Theta)-I)\b{b}^a\}_i\]\delta\lambda^a_i\\\;\;\;\;\; +$-\lambda^a_i$\delta U_i + \[-\lambda^a_i\{\b{z}\times $R(\Theta)\b{b}^a$\}_i\]\delta\Theta$

よって節点についての等価節点内力は次のようになる．

$\{\begin{array}{l}\{Q_u\}^a_i = \frac{\partial W}{\partial u^a_i}+\lambda^a_i \\ \{Q_\lambda\}^a_i = u^a_i-U_i-\{(R(\Theta)-I)\b{b}^a\}_i\\ \{Q_U\}_i = -\lambda^a_i\\ \{Q_\Theta\}_i = -\lambda^a_i\{\b{z}\times $R(\Theta)\b{b}^a$\}_i\end{array}$

剛体の並進や回転についての最終的な内力は全ての拘束された節点からの内力の重ね合わせであることに注意したい．

$\{\begin{array}{l}\{Q_U\}_i = -\sum_k^n\lambda^{a(k)}_i\\ \{Q_\Theta\}_i = -\sum_k^n\lambda^{a(k)}_i\{\b{z}\times $R(\Theta)\b{b}^{a(k)}$\}_i\end{array}$

接線剛性行列の計算

接線剛性行列は内力を微分することで得られる．上三角行列は以下のとおりである．対象行列になるから下三角行列は上三角の転置をすればよい．

$[K_{uu}]^{ab}_{ij}=\frac{\partial \{Q_u\}^a_i}{\partial u^b_j} = \frac{\partial^2 W}{\partial u^a_i\partial u^b_j},\;\;[K_{u\lambda}]^{ab}_{ij}=\frac{\partial \{Q_u\}^a_i}{\partial \lambda^b_j} = \delta_{ab}\delta_{ij}$

$[K_{uU}]^{a\;}_{ij}=\frac{\partial \{Q_u\}^a_i}{\partial U_j} = 0,\;\;[K_{u\Theta}]^{a\;}_{i\;}=\frac{\partial \{Q_u\}^a_i}{\partial\Theta} = 0$

$[K_{\lambda\lambda}]^{ab}_{ij} = \frac{\partial \{Q_\lambda\}^a_i}{\partial \lambda^b_j} = 0,\;\;\;[K_{\lambda U}]^{a\;}_{ij} = \frac{\partial \{Q_\lambda\}^a_i}{\partial U_j} = -\delta_{ij},\;\;[K_{\lambda\Theta}]^{a\;}_{i\;} = \frac{\partial \{Q_\lambda\}^a_i}{\partial\Theta}=-\{\b{z}\times$R(\Theta)\b{b}^a$\}_i$