FEM for Linear Elastic

線形弾性体の有限要素法による解法

Last Update:2009年05月15日

目次
線形弾性体
有限要素法離散化
- 積分領域分割
- 内挿関数の導入
要素における離散化
- アイソパラメトリック要素
テンソルのベクトル表記
２次元問題
- 平面歪
- 平面応力
簡単な２次元問題の計算例
- ２次元単純引っ張り問題
線形弾性体の解析をするときに注意すべき４つの点
数学的なトピック
- 解の一意性存在性
参考にしたもの
- Links
- Books

線形弾性体

線形弾性体における歪

線形弾性体では線形歪 $\epsilon$ を次のように表す。

$\b{\epsilon}=\frac{1}{2}(\nabla_X\otimes\b{u}+\b{u}\otimes\nabla_X)$

$\epsilon_{ij}=\frac{1}{2}(\frac{\partial u_i}{\partial X_j}+\frac{\partial u_j}{\partial X_i})$

ここで $\b{u}$ は無変形状態からの変位である。

線形弾性体の構成式

等方な線形弾性体の応力 $\b{\sigma}$ は線形な歪をもとにして次のように書ける。

$\b{\sigma}=\lambda(\tr\b{\epsilon})\b{I}+2\mu\b{\epsilon}$

但し、 $\lambda$ 、 $\mu$ は Rame の定数である。これを成分で書くと次のとおり、

$\sigma_{ij}=\lambda\epsilon_{kk}\delta_{ij}+2\mu\epsilon_{ij}$

また、 $\lambda$ 、 $\mu$ はヤング率やポアソン比 $\nu$ と次のような関係がある。

$\lambda=\frac{E\nu}{(1+\nu)(1-2\nu)}$ 、 $\mu=\frac{E}{2(1+\nu)}$

問題設定

S1上では変位が固定されている。

$u=\bar{u} \quad ( \quad on \quad S1 \quad )$

このような境界条件を固定境界条件、変位境界条件と呼ぶ。

S2上では応力がかかっている。

$\b{\sigma}^T\cdot\b{n}=\b{t} \quad ( \quad on \quad S2 \quad )$

このような境界条件を応力境界条件と呼ぶ。

弱形式化

線形弾性体では基本的に平衡方程式を変形して弱形式化を行うが、そこでは数々の近似を行う。大きな変形を取り扱う場合は元の平衡方程式を大きく変えてしまうのでずれてしまう。しかし、微小な変形ではその影響が少ない。

Cauchyの第一原理より

$\rho\left.\frac{\partial v}{\partial t}\right|_X=\rho\b{g}+\nabla\cdot\b{\sigma}$

静的な釣り合い状態にある物体は加速度が０なので次の式を満たす

$-\nabla\cdot\b{\sigma}=\rho\b{g}$

これを弱形式化するために、 S_1 上で０となる任意の関数 $\delta u$ を両辺に掛け、変形前の領域で積分してみる。

$-\int_V\delta u\cdot(\nabla\cdot\b{\sigma})dV=\int_V\delta u\cdot\rho\b{g}dV$

左辺第一項の被積分関数について変形を行う

$\delta u\cdot(\nabla\cdot\b{\sigma})=\delta u_j\frac{\partial\sigma_{ij}}{\partial x_i}\sime\delta u_j\frac{\partial\sigma_{ij}}{\partial X_i}=\frac{\partial}{\partial X_i}(\delta u_j\sigma_{ij})-\frac{\partial\delta u_j}{\partial X_i}\sigma_{ij}\\ \qquad\qquad\qquad\qquad =\frac{\partial}{\partial X_i}(\delta u_j\sigma_{ij})-\frac{1}{2}(\frac{\partial\delta u_j}{\partial X_i}+\frac{\partial\delta u_i}{\partial X_j})\sigma_{ij}=\frac{\partial}{\partial X_i}(\delta u_j\sigma_{ij})-\delta\epsilon_{ij}\sigma_{ij}\\ \qquad\qquad\qquad\qquad =\nabla\cdot(\sigma\cdot\delta\b{u})-\delta\b{\epsilon}:\b{\sigma}$

これを代入すると

$-\int_V\nabla\cdot(\sigma\cdot\delta\b{u})-\delta\b{\epsilon}:\b{\sigma}dV=\int_V\delta u\cdot\rho\b{g}dV$

左辺の被積分関数第１項を右辺に移動させて

$\int_V\delta\b{\epsilon}:\b{\sigma}dV=\int_V\delta u\cdot\rho\b{g}dV+\int_V\nabla\cdot(\sigma\cdot\delta\b{u})dV$

ガウスの発散定理を右辺第２項に適応して、

$\int_V\b{\sigma}:\delta\b{\epsilon}dV=\int_V\delta u\cdot\rho\b{g}dV+\int_{\partial V}N\cdot(\sigma\cdot\delta\b{u})dS$

右辺第二項について変形を行う。

$\int_{\partial V}N\cdot(\sigma\cdot\delta\b{u})dS=\int_{S_2}N\cdot(\sigma\cdot\delta\b{u})dS\sime\int_{S_2}\b{n}\cdot(\sigma\cdot\delta\b{u})dS=\int_{S_2}\delta\b{u}\cdot\sigma^T\cdot\b{n}dS=\int_{S_2}\delta\b{u}\cdot\b{t}dS$

これを代入すると最終的に弱形式化された問題は次のようになる。

弱形式化された支配方程式
$\{\begin{array}{l}\int_V\b{\sigma}:\delta\b{\epsilon}dV=\int_V\rho\delta\b{u}\cdot\b{g}dV+\int_{S_2}\delta\b{u}\cdot\b{t}dS\quad\{ \delta\b{u} \mid \delta\b{u}=0 \quad (on \quad S_1) \}\\ \b{u}=\bar{\b{u}}\qquad (\quad on \quad S_1 \quad)\end{array}$

変位を用いた表示への弱形式化された支配方程式の変形

上の式で弱形式化はできたわけであるが、変位を変数として解くので、上の弱形式の方程式を変位が入った式に変形しなければならない。

応力に線形弾性体の構成式を代入して、

$\int_V(\lambda(\tr\b{\epsilon})\b{I}+2\mu\b{\epsilon}):\delta\b{\epsilon}dV=\int_V\rho\delta\b{u}\cdot\b{g}dV+\int_{S_2}\delta\b{u}\cdot\b{t}dS$

$\int_V \lambda(\tr\b{\epsilon})(\tr\b{\delta\epsilon})+2\mu\b{\epsilon}:\delta\b{\epsilon}dV=\int_V\rho\delta\b{u}\cdot\b{g}dV+\int_{S_2}\delta\b{u}\cdot\b{t}dS$

、に総和規約を適応して成分で書くと次のようになる。

$\int_V \lambda\epsilon_{jj}\delta\epsilon_{ii}+2\mu\epsilon_{ij}\delta\epsilon_{ij}dV=\int_V\rho\delta u_i g_idV+\int_{S_2}\delta u_i t_idS$

$\int_V \lambda\frac{\partial u_j}{\partial X_j}\frac{\partial \delta u_i}{\partial X_i}+2\mu\frac{1}{2}$\frac{\partial u_i}{\partial X_j}+\frac{\partial u_j}{\partial X_i}$\frac{1}{2}$\frac{\partial \delta u_i}{\partial X_j}+\frac{\partial \delta u_j}{\partial X_i}$dV=\int_V\rho\delta u_i g_idV+\int_{S_2}\delta u_i t_idS$

左辺被積分関数中の第２項を展開して

$\int_V \lambda\frac{\partial u_j}{\partial X_j}\frac{\partial \delta u_i}{\partial X_i}+\frac{1}{2}\mu$\frac{\partial u_i}{\partial X_j}\frac{\partial \delta u_i}{\partial X_j} + \frac{\partial u_j}{\partial X_i}\frac{\partial \delta u_i}{\partial X_j} + \frac{\partial u_i}{\partial X_j}\frac{\partial \delta u_j}{\partial X_i} + \frac{\partial u_j}{\partial X_i}\frac{\partial \delta u_j}{\partial X_i}$dV=\int_V\rho\delta u_i g_idV+\int_{S_2}\delta u_i t_idS$

$\delta u$ の添え字がにの添え字がになるように添え字を入れ替えると次のとおり

変位を元に弱形式化された支配方程式
$\{\begin{array}{l}\int_V \lambda\frac{\partial u_j}{\partial X_j}\frac{\partial \delta u_i}{\partial X_i} + \mu\(\frac{\partial u_j}{\partial X_k}\frac{\partial \delta u_i}{\partial X_k}\delta_{ij} + \frac{\partial u_j}{\partial X_i}\frac{\partial \delta u_i}{\partial X_j} \)dV=\int_V\rho\delta u_i g_idV+\int_{S_2}\delta u_i t_idS\quad\{ \delta\b{u} \mid \delta\b{u}=0 \quad (on \quad S_1) \}\\ \b{u}=\bar{\b{u}}\qquad (\quad on \quad S_1 \quad)\end{array}$

変位を元に弱形式化された支配方程式

$\{\begin{array}{l}\int_V \lambda\frac{\partial u_j}{\partial X_j}\frac{\partial \delta u_i}{\partial X_i} + \mu$\frac{\partial u_j}{\partial X_k}\frac{\partial \delta u_i}{\partial X_k}\delta_{ij} + \frac{\partial u_j}{\partial X_i}\frac{\partial \delta u_i}{\partial X_j} $dV=\int_V\rho\delta u_i g_idV+\int_{S_2}\delta u_i t_idS\quad\{ \delta\b{u} \mid \delta\b{u}=0 \quad (on \quad S_1) \}\\ \b{u}=\bar{\b{u}}\qquad (\quad on \quad S_1 \quad)\end{array}$

有限要素法離散化

積分領域分割

$\int_V \lambda\frac{\partial u_j}{\partial X_j}\frac{\partial \delta u_i}{\partial X_i} + \mu$\frac{\partial u_j}{\partial X_k}\frac{\partial \delta u_i}{\partial X_k}\delta_{ij} + \frac{\partial u_j}{\partial X_i}\frac{\partial \delta u_i}{\partial X_j} $dV=\int_V\rho\delta u_i g_idV+\int_{S_2}\delta u_i t_idS$

上式は積分で書かれている。積分とはつまり和であるので積分領域を分割してた中で積分を実行し、それを足し合わせて上式を計算してもよい。

そこでを要素分割した領域を V_e 、 S_2 を要素分割した領域を ${S_2}_e$ とすると定式は次のように書ける。

$\sum_e^{nV_e}\int_{V_e} \lambda\frac{\partial u_j}{\partial X_j}\frac{\partial \delta u_i}{\partial X_i} + \mu$\frac{\partial u_j}{\partial X_k}\frac{\partial \delta u_i}{\partial X_k}\delta_{ij} + \frac{\partial u_j}{\partial X_i}\frac{\partial \delta u_i}{\partial X_j} $dV = \sum_e^{nV_e}\int_{V_e}\rho\delta u_i g_idV + \sum_e^{nS_2_e}\int_{S_e}\delta u_i t_idS$

但し、 nV_e 、 nS_2_e はそれぞれと S_2_e の要素分割数である。

内挿関数の導入

V_e 内で関数 $u_j,\delta u_i$ は次のような形状関数によって離散化されているとする。
但し、固定境界条件が設定されている面 S_1 上の節点 $\bar{n}$ では $u_j^{\bar{n}}=g_1$ 、 $\delta u_i^{\bar{n}}=0$ である。

u_j = N^n u_j^n 、 $\delta u_i = N^m\delta u_i^m$

同様に S_2_e 内で関数 $\b{u},\delta\b{u}$ は次のような形状関数 $\bar{N}$ によって離散化されているとする。

$u_j = \bar{N}^n u_j^n$ 、 $\delta u_i = \bar{N}^m\delta u_i^m$

これを上式に代入すると次のようになる。

$\sum_e^{nV_e}\int_{V_e} \lambda\frac{\partial \b{N}^n u^n_j}{\partial X_j}\frac{\partial \b{N}^m\delta u^m_i}{\partial X_i} + \mu\frac{\partial \b{N}^n u^n_j}{\partial X_k}\frac{\partial \b{N}^m \delta u^m_i}{\partial X_k}\delta_{ij} + \mu\frac{\partial \b{N}^n u^n_j}{\partial X_i}\frac{\partial \b{N}^m \delta u^m_i}{\partial X_j} dV \\ \qquad \qquad = \sum_e^{nV_e}\int_{V_e}\rho \b{N}^m \delta u^m_i g_idV + \sum_e^{nS_2_e}\int_{S_e} \bar{\b{N}}^m \delta u^m_i t_idS$

ここで $u_j^n,\delta u_i^m$ は節点の値であり，関数ではないので積分の外に出すことができる。それぞれ積分の外に出した後にまとめると次のようになる。

$\delta u^m_i$\sum_e^{nV_e}\int_{V_e} \lambda\frac{\partial \b{N}^n }{\partial X_j}\frac{\partial \b{N}^m }{\partial X_i} + \mu\frac{\partial \b{N}^n}{\partial X_k}\frac{\partial \b{N}^m}{\partial X_k}\delta_{ij} + \mu\frac{\partial \b{N}^n}{\partial X_i}\frac{\partial \b{N}^m \delta}{\partial X_j} dV $u^n_j \\ \qquad \qquad = \delta u^m_i $ \sum_e^{nV_e}\int_{V_e}\rho \b{N}^m g_idV + \sum_e^{nS_2_e}\int_{S_e} \bar{\b{N}}^m t_idS$$

これは次のように行列表記できる。

$\delta u_i^m \quad K^{m,n}_{i,j} \quad u_j^n=\delta u_i^m F^m_i$

$K^{m,n}_{i,j} = \sum_e^{nV_e}{K_e}^{a,b}_{i,j}$ （但し、要素内節点番号a,bは全体節点番号m,n)

線形弾性体の要素剛性行列
${K_e}^{a,b}_{i,j}=\int_{V_e} \lambda\frac{\partial \b{N}^b }{\partial X_j}\frac{\partial \b{N}^a }{\partial X_i} + \mu\frac{\partial \b{N}^b}{\partial X_k}\frac{\partial \b{N}^a}{\partial X_k}\delta_{ij} + \mu\frac{\partial \b{N}^b}{\partial X_i}\frac{\partial \b{N}^a}{\partial X_j} dV$

$F^m_i = \sum_e^{nV_e}\int_{V_e}\rho \b{N}^m g_idV + \sum_e^{nS_2_e}\int_{S_e} \bar{\b{N}}^m t_idS$

要素における離散化

アイソパラメトリック要素

アイソパラメトリック要素では積分点 $\alpha$ における被積分関数を計算し、それぞれヤコビアンと重み $\omega_{\alpha}$ をかけて、積分点ごとに足し合わせることで積分を行う。

${K_e}^{a,b}_{i,j}=\int_{V_e} \lambda\frac{\partial \b{N}^b }{\partial X_j}\frac{\partial \b{N}^a }{\partial X_i} + \mu\frac{\partial \b{N}^b}{\partial X_k}\frac{\partial \b{N}^a}{\partial X_k}\delta_{ij} + \mu\frac{\partial \b{N}^b}{\partial X_i}\frac{\partial \b{N}^a}{\partial X_j} dV\\ \qquad\qquad\qquad =\sum_{\alpha}\omega_{\alpha}$\lambda\frac{\partial \b{N}^b }{\partial X_j}\frac{\partial \b{N}^a }{\partial X_i} + \mu\frac{\partial \b{N}^b}{\partial X_k}\frac{\partial \b{N}^a}{\partial X_k}\delta_{ij} + \mu\frac{\partial \b{N}^b}{\partial X_i}\frac{\partial \b{N}^a}{\partial X_j}$J_{\alpha}$

もちろん被積分関数は積分ごとに異なる値をとる。

積分点ごとに $\frac{\partial N}{\partial X}$ を計算して、被積分関数を求めなければならない。

プログラミング例

積分ごとの値を足し合わせる部分のプログラムを参考までに載せておく。

記号の対応は以下のとおり

myu= $\mu$ 、lambda= $\lambda$ 、rho= $\rho$ 、g[i]=
dndx[a][i]= $\frac{\partial N^a}{\partial X_i}$ 、an[a]=、detwei= $\omega_{\alpha}J_{\alpha}$
emat[a][b][i][j]= ${K_e}^{a,b}_{i,j}$

// 要素剛性行列を作る
for(unsigned int inoel=0;inoel<nnoel;inoel++){
for(unsigned int jnoel=0;jnoel<nnoel;jnoel++){
   double dtmp1 = 0.0;
   for(unsigned int idim=0;idim<ndim;idim++){
      for(unsigned int jdim=0;jdim<ndim;jdim++){
         emat[inoel][jnoel][idim][jdim] 
            += detwei*( lambda*dndx[inoel][idim]*dndx[jnoel][jdim]+myu*dndx[jnoel][idim]*dndx[inoel][jdim] );
      }
      dtmp1 += dndx[inoel][idim]*dndx[jnoel][idim];
   }
   for(unsigned int idim=0;idim<ndim;idim++){
      emat[inoel][jnoel][idim][idim] += detwei*myu*dtmp1;
   }
}
}
// 要素内外力を作る
for(unsigned int inoel=0;inoel<nnoel;inoel++){
   for(unsigned int idim=0;idim<ndim;idim++){
      	eforce[inoel][idim] += g[idim]*rho*an[inoel]*detwei;
   }
}

テンソルのベクトル表記

Cauchy応力はCauchyの第二原理から対称テンソルである。また線形歪も定義から明らかに対称テンソルである。つまり、

$\sigma_{ij}=\sigma_{ji}$ 、 $\epsilon_{ij}=\epsilon_{ji}$

テンソルはベクトルからベクトルへの線形変換であったから、行列として成分表示できる。この時の成分の数は３次元なら９個である。

しかし、このような対称テンソルの場合は独立な成分の数は６つなので次のように独立な成分の数をベクトル的に並べると、圧縮して書くことができ何かと便利である。

$\{\b{\sigma}\}=$\begin{array}\sigma_{xx}\\ \sigma_{yy}\\ \sigma_{zz}\\ \sigma_{xy}\\ \sigma_{xz}\\ \sigma_{yz}\end{array}$=$\begin{array}\sigma_{xx}\\ \sigma_{yy}\\ \sigma_{zz}\\ \tau_{xy}\\ \tau_{xz}\\ \tau_{yz}\end{array}$$ 、 $\{\b{\epsilon}\}=$\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \epsilon_{zz}\\ 2\epsilon_{xy}\\ 2\epsilon_{xz}\\ 2\epsilon_{yz}\end{array}$=$\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \epsilon_{zz}\\ \gamma_{xy}\\ \gamma_{xz}\\ \gamma_{yz}\end{array}$$

剪断歪の場合だけ歪が２倍して表記していることに注意していただきたい。このように $\epsilon$ の剪断部分を２倍した $\gamma$ を使ってベクトル表記した歪を工学歪と呼ばれる。工学では専らこちらの歪が用いられる。

剪断歪の部分を２倍にした工学歪を使うと、通常は応力テンソルと歪テンソルのテンソル積で書かれる歪エネルギー密度 $\rho_{W}$ を、ベクトルの内積で書くことができる。

$\rho_{\b{W}}=\frac{1}{2}\b{\sigma}:\b{\epsilon}=\frac{1}{2}\sigma_{ij}\epsilon_{ij}=\frac{1}{2}\{\b{\sigma}\}\cdot\{\b{\epsilon}\}$

線形弾性体の応力-歪関係式は次のような関係であった。

$\sigma_{ij}=\lambda\epsilon_{kk}\delta_{ij}+2\mu\epsilon_{ij}$

これを添え字を入れ替えて、 $\epsilon$ の添え字が k,l になるようにすると

$\sigma_{ij}=\lambda\epsilon_{kl}\delta_{kl}\delta_{ij}+2\mu\epsilon_{kl}\delta_{ik}\delta_{jl}=(\lambda\delta_{kl}\delta_{ij}+2\mu\delta_{ik}\delta_{jl})\epsilon_{kl}=C_{ijkl}\epsilon_{kl}$

ここで応力と歪を関係づける、４階のテンソル $\b{C}$ は構成則テンソルと呼ばれる。

これらを利用すると、応力、歪をテンソル表記からベクトル表記に変えた場合に応力-歪関係式は次のようになる。

$\begin{array}\sigma_{xx}\\ \sigma_{yy}\\ \sigma_{zz}\\ \tau_{xy}\\ \tau_{xz}\\ \tau_{yz}\end{array}\)= \[\begin{array} \lambda+2\mu&&\lambda&&\lambda\\ \lambda&&\lambda+2\mu&&\lambda\\ \lambda&&\lambda&&\lambda+2\mu\\ && && && \mu&& && \\ && && && &&\mu&& \\ && && && && &&\mu \end{array}\] \(\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \epsilon_{zz}\\ \gamma_{xy}\\ \gamma_{xz}\\ \gamma_{yz}\end{array}$

２次元問題

平面歪

z方向の厚みが大きい場合などは、変位は２次元的であると考えられる。つまり、z方向の変位は小さいと考えられる。またx変位やｙ変位はz方向に対して一定となると考えられる。このような状態を平面歪状態と呼ぶ。

つまり、 u_z=0 、 $\frac{\partial u_x}{\partial X_z}=0$ 、 $\frac{\partial u_y}{\partial X_z}=0$ が成り立つ。

これを用いると、 $\epsilon_{zz}=0$ 、 $\gamma_{xz}=0$ 、 $\gamma_{yz}=0$ であることがわかる。

これをもちいて歪エネルギー密度 $\rho_{W}$ を計算する。

$\rho_{\b{W}}=\frac{1}{2}\{\b{\sigma\}\cdot\{\b{\epsilon\}= \frac{1}{2}$\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \epsilon_{zz}\\ \gamma_{xy}\\ \gamma_{xz}\\ \gamma_{yz}\end{array}$^T$\begin{array}\sigma_{xx}\\ \sigma_{yy}\\ \sigma_{zz}\\ \tau_{xy}\\ \tau_{xz}\\ \tau_{yz}\end{array}$= \frac{1}{2}$\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \epsilon_{zz}\\ \gamma_{xy}\\ \gamma_{xz}\\ \gamma_{yz}\end{array}$^T \[\begin{array} \lambda+2\mu&&\lambda&&\lambda\\ \lambda&&\lambda+2\mu&&\lambda\\ \lambda&&\lambda&&\lambda+2\mu\\ && && && \mu&& && \\ && && && &&\mu&& \\ && && && && &&\mu \end{array}\] $\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \epsilon_{zz}\\ \gamma_{xy}\\ \gamma_{xz}\\ \gamma_{yz}\end{array}$$

ここで、 $\epsilon_{zz}=0$ 、 $\gamma_{xz}=0$ 、 $\gamma_{yz}=0$ をこの式に代入すると、

$\rho_{\b{W}}=\frac{1}{2}$\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ 0\\ \gamma_{xy}\\ 0\\ 0\end{array}$^T \[\begin{array} \lambda+2\mu&&\lambda&&\lambda\\ \lambda&&\lambda+2\mu&&\lambda\\ \lambda&&\lambda&&\lambda+2\mu\\ && && && \mu&& && \\ && && && &&\mu&& \\ && && && && &&\mu \end{array}\] $\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ 0\\ \gamma_{xy}\\ 0\\ 0\end{array}$= \frac{1}{2}$\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \gamma_{xy}\end{array}$^T \[\begin{array} \lambda+2\mu&&\lambda&&\\ \lambda&&\lambda+2\mu&&\\ && && && \mu\\ \end{array}\] $\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \gamma_{xy}\end{array}$$

元の３次元の式と比べると、Rameの定数を変えることなく単純に次元を３から２に減らせばいいことが分かる。

平面応力

ｚ方向の厚みが十分小さい場合は、平面応力

$\sigma_{zz}=0$ 、 $\tau_{xz}=0$ 、 $\tau_{yz}=0$ が成り立つ。

歪についての関係を求めるために、次の応力-歪関係式から歪を逆算しよう。

$\begin{array}\sigma_{xx}\\ \sigma_{yy}\\ 0\\ \tau_{xy}\\ 0\\ 0\end{array}\)= \[\begin{array} \lambda+2\mu&&\lambda&&\lambda\\ \lambda&&\lambda+2\mu&&\lambda\\ \lambda&&\lambda&&\lambda+2\mu\\ && && && \mu&& && \\ && && && &&\mu&& \\ && && && && &&\mu \end{array}\] \(\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \epsilon_{zz}\\ \gamma_{xy}\\ \gamma_{xz}\\ \gamma_{yz}\end{array}$

$\epsilon_{zz}=-\frac{\lambda}{\lambda+2\mu}(\epsilon_{xx}+\epsilon_{yy})$ 、 $\gamma_{xz}=0$ 、 $\gamma_{yz}=0$ となる。

$e_{zz}$ を良く見ると負の符号がついていることにより、 $e_{xx},e_{yy}$ によって圧縮(膨張)されたらz方向に膨張(圧縮)されることがわかる。面内で圧縮されると厚み方向に膨らむことがわかる。

これを用いて、歪エネルギー密度 $\rho_{\b{W}}$ を計算すると、

$\rho_{\b{W}}=\frac{1}{2}$\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ -\frac{\lambda}{\lambda+2\mu}(\epsilon_{xx}+\epsilon_{yy})\\ \gamma_{xy}\\ 0\\ 0\end{array}$^T \[\begin{array} \lambda+2\mu&&\lambda&&\lambda\\ \lambda&&\lambda+2\mu&&\lambda\\ \lambda&&\lambda&&\lambda+2\mu\\ && && && \mu&& && \\ && && && &&\mu&& \\ && && && && &&\mu \end{array}\] $\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ -\frac{\lambda}{\lambda+2\mu}(\epsilon_{xx}+\epsilon_{yy})\\ \gamma_{xy}\\ 0\\ 0\end{array}$\\ \qquad\qquad\qquad=\frac{1}{2}$\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \gamma_{xy}\end{array}$^T \[\begin{array} \lambda'+2\mu&&\lambda'&&\\ \lambda'&&\lambda'+2\mu&&\\ && && && \mu\\ \end{array}\] $\begin{array}\epsilon_{xx}\\ \epsilon_{yy}\\ \gamma_{xy}\end{array}$$

となる。但し、 $\lambda'=\frac{2\lambda\mu}{\lambda+2\mu}$ である。

Rameの定数のうち、λを見かけ上変化させた上で３次元から２次元化すればいいことがわかる。

簡単な２次元問題の計算例

簡単な形状をしていて、一様な歪を生じるような問題は解析的に解くことが可能である。このような単純な問題を解くことで解析プログラムが本当に正しいのか検証することができる。

２次元単純引っ張り問題

次の図のように矩形の物体を引っ張って変形させる。

２次元単純引っ張り

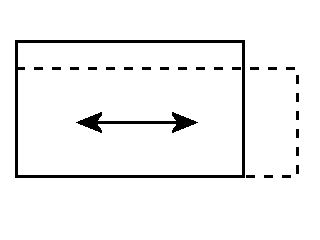x方向に引っ張るとするとｙ方向には力が働かないのでｙ方向の垂直応力は０となる。

$\sigma_{yy}=0$

平面歪問題

$\sigma_{yy}=\lambda\epsilon_{xx}+(\lambda+2\mu)\epsilon_{yy}+\lambda\epsilon_{zz}=\lambda\epsilon_{xx}+(\lambda+2\mu)\epsilon_{yy}=0$ より、

$\epsilon_{yy}=-\frac{\lambda}{\lambda+2\mu}\epsilon_{xx}$ である。

$\nu^*=-\frac{\epsilon_{yy}}{\epsilon_{xx}}=\frac{\lambda}{\lambda+2\mu}=\frac{\nu}{1-\nu}$ となる。

$\sigma_{xx}=(\lambda+2\mu)\epsilon_{xx}+\lambda\epsilon_{yy}=(\lambda+2\mu)\epsilon_{xx}+\lambda(-\frac{\lambda}{\lambda+2\mu})\epsilon_{xx}=\frac{4\mu(\lambda+\mu)}{\lambda+2\mu}\epsilon_{xx}$

これから、見かけ上のヤング率 E^* は

$E^*=\frac{\sigma_{xx}}{\epsilon_{xx}}=\frac{4\mu(\lambda+\mu)}{\lambda+2\mu}=\frac{E}{1-\nu^2}$

平面応力状態

平面応力状態では $\sigma_{zz}=0$ であり、

これは３次元の単純引っ張りと一致する。

よって

$\nu^*=\nu$ 、 E^*=E

である。

線形弾性体の解析をするときに注意すべき４つの点

線形弾性体の解析において注意することを４つほどあげると次のようになる。

ポアソン比が0.5に近づくと解の精度がおちる。
曲げ問題は要素の種類によっては解の精度がわるい
変形,歪,応力はは実際より小さく評価される。
物体が回転する問題はメッシュが膨張して非現実的な解を得る。

以下それぞれの注意点について簡単に述べる。

ポアソン比が0.5に近づくと解の精度が落ちる問題について

ポアソン比が0.5に近づけると体積弾性率が無限に大きくなる。これは体積変化に対する反力が大きくなることを意味しており、体積変化がないという非圧縮性の拘束条件が次第に変位に付加される。

このような非圧縮の問題の場合、応力は変位から発生する応力の他に拘束力から発生する非決定応力が追加されるため、変位のみを変数として解析することがでない。そこで圧力変数を導入してこの問題を解析する。変位変数と圧力変数を用いた弾性体の解析をu/p formulationという。圧力変数を導入するために圧力節点を追加するが、圧力節点と変位節点の要素内の配置の仕方に解析がうまくパターンがあるのでそれらを採用しなければならない。

曲げ問題は要素の種類によっては解の精度が悪い問題について

1次要素など補間関数の次数が低いときに梁など薄い構造物の曲げを解析するときに、実際よりも硬い解が得られる。これはメンブレンロッキングと呼ばれる現象で注意が必要である。

これも梁のような薄い構造物を曲げるときに面外剪断が０であるというKirchhoff条件が変位に付加させるために解の精度が悪くなってしまうのである。

高次要素を用いたり、低減積分、選択的低減積分を用いることで精度を向上させることができる。またソリッド要素をやめて構造要素を用いるのも有効な手段の一つである。

２次元梁曲げ問題のロッキング問題については以下が詳しい。

有限要素法における2 次元弾性体要素の精度に関する研究: http://globe.nagaokaut.ac.jp/yoshisyu/2003/kensetu/pdf/ken04607.pdf

変形,歪,応力が実際より小さくに評価される問題について

変分原理より解析解は最もポテンシャルエネルギーの低い解である。有限要素法で求める解はメッシュ上で表現できる関数に限定して、その中でもっともエネルギーの小さな解である。よって有限要素法のエネルギーは解析解のエネルギーより常に大きい。これは大雑把に言えば、有限要素法の変形や歪や応力は解析解の変形よりも小さく評価されることを意味している。有限要素法による弾性体解析の一つの目的は構造部材が破壊するかどうかである。実際よりも破壊されにくいというように評価されてしまう。これは危険である。異なるメッシュサイズの解析を行って収束を見るなど、十分に注意しなければならない。

物体が回転する問題はメッシュが膨張して非現実的な解を得る問題について

線形弾性体の構成式は客観性をみたしていないので回転することは想定外である。線形弾性体を回転させた場合は膨張するような解が得られる。

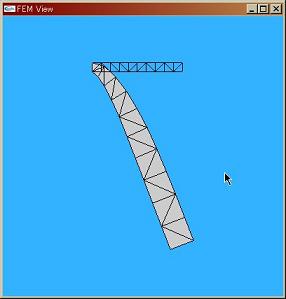
下の図は線形弾性体の片持ち梁に下向きの重力をかけて曲げたものである。回転した部分が大きく膨張して非現実的な変形をしているのがわかる。

線形弾性体を回転させた場合の膨張

解析ソースコード >>>>LinearSolid_UnsTri.zip

そもそも線形弾性体は微小変形微小歪問題にのみ用いるべきである。微小歪問題で大変形（つまり回転）にも対応しているのがサンブナン体である。

線形弾性体の回転の詳しい解析

２次元の線形弾性体を剛体回転させた場合どうなるのかを詳しく調べてみよう。

点 (X,Y) を原点反時計周りに $\theta$ だけ剛体回転させた場合の座標 (x,y) は、

$(x,y)=(X\cos\theta-Y\sin\theta,X\sin\theta+Y\cos\theta)$

回転させる前の点からの変位 u_x,u_y は

$(u_x,u_y)=(x-X,y-Y)=(X(\cos\theta-1)-Y\sin\theta,X\sin\theta+Y(\cos\theta-1))$

よって線形歪は次のようになる。

$\epsilon_{xx}=\frac{\partial u_x}{\partial X}=\cos\theta-1$

$\epsilon_{yy}=\frac{\partial u_y}{\partial Y}=\cos\theta-1$

$\gamma_{xy}=\frac{\partial u_x}{\partial Y}+\frac{\partial u_y}{\partial X}=0$

よって $\epsilon_{xx}=\epsilon_{yy}<0$ より等方圧縮の垂直歪が発生していることがわかる。垂直圧縮することで膨張させようとする応力が働く。梁の回転している部分には応力がかかっていないので、応力を０にするために結局、膨張した解を得ることになる。

数学的なトピック

ノルムを次のように定義する

$||\epsilon(v)||^2_0=\int_{\Omega}\epsilon(v):\epsilon(v)d\Omega$

$||v||^2_0=\sum_{i=1}^N \int_\Omega v_i^2 d\Omega$

$||v||^2_1=||v||^2_0+\sum_{i=1}^N||\nabla v_i||^2_0$

弱形式の線形弾性体は次のとおり

$\int_{\Omega} A \epsilon(u):e(\phi)d\Omega = <f,\phi>_{H^{-1},H^1(\Omega)^N}\qquad\qquad\forall\phi\in H^1_\Gamma(\Omega)^N$

ここで $\phi$ にを代入して、の強圧性より

$\alpha||\epsilon(u)||^2_0\le\int_{\Omega} A \epsilon(u):\epsilon(u)d\Omega = <f,u>_{H^{-1},H^1(\Omega)^N} \le ||f||_{H^{-1}} ||u||_1$

解の一意性存在性

Kornの第一不等式よりが成り立つ。

$c||v||^2_1\le ||v||^2_0+||\epsilon(v)||^2_0\qquad\qquad\forall v\in H^1(\Omega)^N$

Kornの第二不等式

$c'||v||^2_1\le ||\epsilon(v)||^2_0\qquad\qquad\forall v\in H^1_{\Gamma}(\Omega)^N$

が成り立つことを背理法で示す。もし上が成り立たないとすると、

||v_n||_1 = 1 を満たしたまま

$\lim_{n\rightarrow \infty}||\epsilon(v_n)||_0=0$ とすような v_n が存在する。これを仮定して矛盾が起こることを示す。

Sovlevの埋蔵定理より H^1 空間は L^2 空間でコンパクトである。よって、

$v_n \rightarrow v$ strongly in $L^2(\Omega)^N$

となるような $v\in H^1_\Gamma(\Omega)^N$ が存在する。

ここでKornの不等式より

$c||v_n-v_m||^2_1\le ||v_n-v_m||^2_0+||\epsilon(v_n-v_m)||^2_0\\\qquad\qquad\qquad\qquad\qquad\le ||v_n-v_m||^2_0+||\epsilon(v_n)||^2_0+||\epsilon(v_m)||^2_0$

n,m を大きくすれば右辺は好きなだけ小さくできる。よって v_n は $H^1(\Omega)^N$ 上のCauchy列である。よって v_n はに $H^1(\Omega)^N$ で収束する。

$||\epsilon(v)||_0=\lim_{n\rightarrow \infty}||\epsilon(v_n)||_0=0$ であるから $\epsilon(v)=0$ である。

は境界 $\Gamma$ 上で０であるから、 v=0 である。

これは ||v_n||_1 = 1 に反する。よって題意は示された。

歪テンソルと変位ののノルムの等価性

逆の不等式が自明であるので $||\phi||_1$ と $||\epsilon(\phi)||_0$ は等価なノルムであるといえる。

つまり、次のように、作用素の H^1 における楕円性がいえる。

$\alpha ||u||^2_1 \le \int_{\Omega} A \epsilon(u):\epsilon(u)d\Omega\le C ||u||^2_1$

このことから、Lax-Milgramの定理より解 $u\in H^1_\Gamma(\Omega)^N$ が唯一に存在することがいえる。

参考にしたもの

Books

非線形有限要素法のためのテンソル解析の基礎	久田俊明　著
連続体力学―簡明な理論と例題 (1979年) (理工学海外名著シリーズ〈31〉)	Ｐ．チャドウィック　著
テンソル解析と連続体力学 (1979年) (理工学海外名著シリーズ〈30〉)	Ｗ．フリューゲ　著

Made by Nobuyuki UMETANI 梅谷　信行

n.umetani@gmail.com