|TOP Page|
弾塑性体や形状最適化問題や接触問題など,制約条件が不等式で表される場合の最適化問題はKuhn-Tucker条件(KKT条件)を使うことができる.Kuhn-Tucker条件はラグランジュ未定乗数法の不等式への拡張である.
次のような問題を考える.
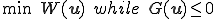
このような解はKuhn-Tucker条件から以下を満たす
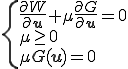
ここでの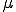 が拘束力を表す.
が拘束力を表す.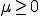 は拘束力が常に負でないこと.
は拘束力が常に負でないこと.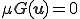 は
は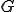 か
か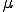 のどちらかが0であることを意味している.例えばある点が壁でさえぎられている場合は、拘束力は壁と反発する方向に壁の上にあるときにしか働かないことに対応している.
のどちらかが0であることを意味している.例えばある点が壁でさえぎられている場合は、拘束力は壁と反発する方向に壁の上にあるときにしか働かないことに対応している.
関数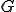 の選び方は幾つも考えられるが
の選び方は幾つも考えられるが
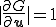
を満たすようにしておくと,
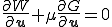
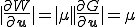
であるから,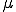 は制約条件の満たされない方向へのエネルギーの勾配の大きさに等しくなる.エネルギーの変位での微分は力であるから,この場合
は制約条件の満たされない方向へのエネルギーの勾配の大きさに等しくなる.エネルギーの変位での微分は力であるから,この場合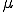 は拘束力の大きさを意味している.このようにLagrange未定乗数に拘束力の大きさとしての意味づけをすることができるので便利である.
は拘束力の大きさを意味している.このようにLagrange未定乗数に拘束力の大きさとしての意味づけをすることができるので便利である.
不等式拘束条件が沢山ある場合はそれぞれ別々に考えればよい.
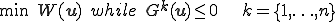
このような解はKuhn-Tucker条件から以下を満たす
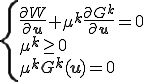
不等式拘束条件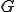 が課されている節点の数が
が課されている節点の数が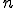 だけあるとする.また,
だけあるとする.また,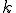 番目の拘束条件の節番号が
番目の拘束条件の節番号が であるとする.
であるとする.
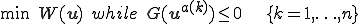
上の議論から有限要素法の解は以下を満たす
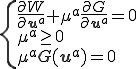
この式が満たされるようにする解法を考えよう
このような条件は非線形なので、反復計算を行い上の式が満たされるようにしなければならない.例えば次のような反復のさせ方が考えられる.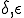 を十分小さな数とする.
を十分小さな数とする.
 なら前回Lagrange未定乗数を入れて計算した結果,今回も
なら前回Lagrange未定乗数を入れて計算した結果,今回も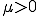 である.だからLagrange未定乗数を入れる.
である.だからLagrange未定乗数を入れる.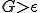 なら,
なら,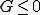 が満たされないので,
が満たされないので,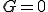 になるように,Lagrange未定乗数を入れる.
になるように,Lagrange未定乗数を入れる.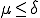 かつ
かつ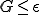 の時は
の時は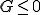 が満たされると考え,Lagrange未定乗数を入れずに、
が満たされると考え,Lagrange未定乗数を入れずに、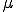 を0にセットする
を0にセットする
これを図にすると図1のようになる.青い場所は接触が起こっているとして、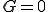 が満たされるようなLagrange未定乗数を入れる場所である.赤い場所は変位について拘束を入れず
が満たされるようなLagrange未定乗数を入れる場所である.赤い場所は変位について拘束を入れず に0をセットする場所である.最終的に黒い線の上に落ち着くことで、
に0をセットする場所である.最終的に黒い線の上に落ち着くことで、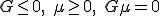 が満たされるようになれば反復終了である.
が満たされるようになれば反復終了である.
条件が不連続的に切り替わる部分は数式で書けば綺麗だが,プログラミング上は誤差とか考慮しなければならない.要は浮動小数点同士の比較は正確にできないので上の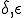 が必要である.この数字はパラーメータスタディによって決めなければならない.
が必要である.この数字はパラーメータスタディによって決めなければならない.
このように2つの状況が不連続に存在する状況では、反復中に2つが交互に入れ替わって収束が遅くなるchatteringという現象が起こる可能性がある.
上の反復法を有限要素法で定式化する時の例を示す.上の反復では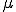 と
と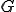 の値によって2つの場合に分けられた.
の値によって2つの場合に分けられた.
次の増分に関する連立一次方程式を解き,解を更新する
![\[\begin{array}{ll}[K_{uu}]^{ab}_{ij}&[K_{u\mu}]^{ab}_{i}\\[K_{\mu u}]^{ab}_{\;j}&[K_{\mu\mu}]^{ab} \end{array}\] \{\begin{array}\{\Delta u\}^b_j\\\{\Delta\mu\}^b\end{array}\} = \{\begin{array}\{f\}^b_j\\0\end{array}\} - \{\begin{array}\{Q_u\}^b_j\\\{Q_\mu\}^b\end{array}\} \[\begin{array}{ll}[K_{uu}]^{ab}_{ij}&[K_{u\mu}]^{ab}_{i}\\[K_{\mu u}]^{ab}_{\;j}&[K_{\mu\mu}]^{ab} \end{array}\] \{\begin{array}\{\Delta u\}^b_j\\\{\Delta\mu\}^b\end{array}\} = \{\begin{array}\{f\}^b_j\\0\end{array}\} - \{\begin{array}\{Q_u\}^b_j\\\{Q_\mu\}^b\end{array}\}](436F6E746163742050726F626C656D2077697468204B75686E2D54756368657220436F6E646974696F6E_eq0038.gif)
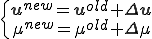
但し,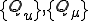 をそれぞれ,変位と拘束力についての等価節点内力であるとした.
をそれぞれ,変位と拘束力についての等価節点内力であるとした.
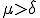 もしくは
もしくは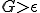 の場合はラグランジュ未定乗数を入れて
の場合はラグランジュ未定乗数を入れて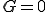 が満たされるようにする.
が満たされるようにする.
内力については次のようになる.
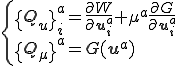
これを微分することで接線剛性行列が得られる
![\{\begin{array}{l}[K_{uu}]^{ab}_{ij}=\frac{\partial \{Q_u\}^a_i}{\partial {u}^b_j} = \frac{\partial^2 W}{\partial\b{u}^a_i\partial\b{u}^b_j}+\mu^a\frac{\partial^2 G}{\partial\b{u}^a_i\partial\b{u}^b_j}\delta_{ab}\\ [K_{u\mu}]^{ab}_{i}=\frac{\partial \{Q_u\}^a_i}{\partial {\mu}^b} = \frac{\partial G}{\partial\b{u}^a_i}\delta_{ab}\\ [K_{\mu u}]^{ab}_{\;j}=\frac{\partial \{Q_\mu\}^a}{\partial u^b_j } = \frac{\partial G}{\partial\b{u}^b_j}\delta_{ab}\\ [K_{\mu \mu}]^{ab}=\frac{\partial \{Q_\mu\}^a}{\partial \mu^b } = 0 \end{array} \{\begin{array}{l}[K_{uu}]^{ab}_{ij}=\frac{\partial \{Q_u\}^a_i}{\partial {u}^b_j} = \frac{\partial^2 W}{\partial\b{u}^a_i\partial\b{u}^b_j}+\mu^a\frac{\partial^2 G}{\partial\b{u}^a_i\partial\b{u}^b_j}\delta_{ab}\\ [K_{u\mu}]^{ab}_{i}=\frac{\partial \{Q_u\}^a_i}{\partial {\mu}^b} = \frac{\partial G}{\partial\b{u}^a_i}\delta_{ab}\\ [K_{\mu u}]^{ab}_{\;j}=\frac{\partial \{Q_\mu\}^a}{\partial u^b_j } = \frac{\partial G}{\partial\b{u}^b_j}\delta_{ab}\\ [K_{\mu \mu}]^{ab}=\frac{\partial \{Q_\mu\}^a}{\partial \mu^b } = 0 \end{array}](436F6E746163742050726F626C656D2077697468204B75686E2D54756368657220436F6E646974696F6E_eq0045.gif)
 かつ
かつ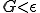 の場合は,節点は拘束力を受けない.よって
の場合は,節点は拘束力を受けない.よって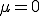 にする.
にする.
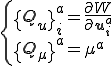
これを微分することで接線剛性行列が得られる
![\{\begin{array}{l}[K_{uu}]^{ab}_{ij}=\frac{\partial \{Q_u\}^a_i}{\partial {u}^b_j} = \frac{\partial^2 W}{\partial\b{u}^a_i\partial\b{u}^b_j}\\ [K_{u\mu}]^{ab}_{i}=\frac{\partial \{Q_u\}^a_i}{\partial {\mu}^b} = 0\\ [K_{\mu u}]^{ab}_{\;j}=\frac{\partial \{Q_\mu\}^a}{\partial u^b_j } = 0\\ [K_{\mu \mu}]^{ab}=\frac{\partial \{Q_\mu\}^a}{\partial \mu^b } = \delta_{ab} \end{array} \{\begin{array}{l}[K_{uu}]^{ab}_{ij}=\frac{\partial \{Q_u\}^a_i}{\partial {u}^b_j} = \frac{\partial^2 W}{\partial\b{u}^a_i\partial\b{u}^b_j}\\ [K_{u\mu}]^{ab}_{i}=\frac{\partial \{Q_u\}^a_i}{\partial {\mu}^b} = 0\\ [K_{\mu u}]^{ab}_{\;j}=\frac{\partial \{Q_\mu\}^a}{\partial u^b_j } = 0\\ [K_{\mu \mu}]^{ab}=\frac{\partial \{Q_\mu\}^a}{\partial \mu^b } = \delta_{ab} \end{array}](436F6E746163742050726F626C656D2077697468204B75686E2D54756368657220436F6E646974696F6E_eq0050.gif)
直線と弾性体との接触を考えてみた.「ある直線よりも節点が上にある」という制約条件は不等式で書き表すことができる.
例えば点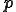 を通り,単位法線ベクトルが
を通り,単位法線ベクトルが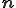 である直線より上にあるという条件は
である直線より上にあるという条件は
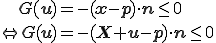
と書ける.但し,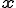 は変位後の点の座標で,
は変位後の点の座標で,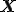 は点の初期座標.
は点の初期座標.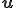 は初期状態からの変位を表す.但し,
は初期状態からの変位を表す.但し,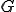 の微分は次のようになる.
の微分は次のようになる.
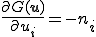
実際にこれらを実装してみたのが以下の動画である.
剛体円との接触を考える.円の外側に節点があると考えればよい.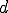 は円の半径で,
は円の半径で,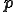 は円の中心の座標とすると,拘束条件の関数
は円の中心の座標とすると,拘束条件の関数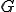 は次のようになる.
は次のようになる.
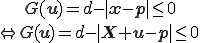
と書ける.但し,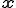 は変位後の点の座標で,
は変位後の点の座標で,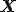 は点の初期座標.
は点の初期座標.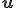 は初期状態からの変位を表す.
は初期状態からの変位を表す.
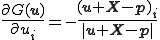
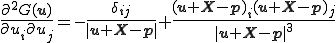
 が非線形性を持っており,2回微分が0にならないことに注意されたい.
が非線形性を持っており,2回微分が0にならないことに注意されたい.
下向きの体積力をかけている線形弾性体の梁に対して左端にリサージュ曲線の強制変位を与えて円と接触させている.
St.Venant-Kirchhoff体でできた梁を自由落下させて剛体円と接触させてみる,有限要素法解析をDelFEMに組み込んで実験してみた.
梁が円に当たってボヨーンと脇に跳ね返った後,回転しながら落ちてゆく.
St.Venant-Kirchhoff体は幾何学的非線形性を考慮した構成式で書かれるために,線形弾性体と違って回転しても不自然な膨張が起こらない.