|TOP Page|
移流拡散方程式とはスカラー量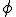 が速度
が速度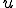 で輸送されつつ,拡散される方程式である。
で輸送されつつ,拡散される方程式である。
物質と同じ速度で動く視点からみれば、輸送の現象は関係ないので、単純な拡散方程式と等価になる。よって移流拡散方程式は次のように書くことができる。
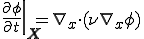
物質時間導関数と空間時間導関数の関係を代入して
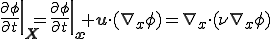
ここで定常であるとういう条件つまり時間的に解が変化しないという条件から、空間時間導関数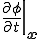 が0であるとして
が0であるとして
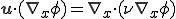
を得るこれが定常移流拡散方程式である。
ひとまず一次元での定常移流拡散方程式を考えた後に多次元(2次元、3次元)に拡張する。
一次元の定常移流拡散のイメージとしては次の図のような状況を考えると分かりやすい。
上の図は一定速度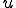 で動くベルトコンベヤーの上流側と下流側に2つの温度が与えられているような図である。この2つの温度が与えられている間の温度の分布は定常移流拡散方程式に従うと考えられる。
で動くベルトコンベヤーの上流側と下流側に2つの温度が与えられているような図である。この2つの温度が与えられている間の温度の分布は定常移流拡散方程式に従うと考えられる。
上式を一次元化すると、一次元の移流拡散方程式は次のとおり
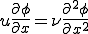
長さが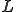 の領域で両端の値が固定されているとき、解は次のようにかける。
の領域で両端の値が固定されているとき、解は次のようにかける。
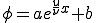
但し変数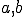 は境界条件を満たすように選ばれる。ここで、
は境界条件を満たすように選ばれる。ここで、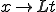 のように
のように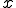 を無次元の長さ
を無次元の長さ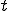 に変換すると解は最終的に次のようにかける。
に変換すると解は最終的に次のようにかける。
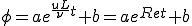
但し、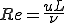 はレイノルズ数である。(本当はuの絶対値を取るのが正しいと思われるがここでは簡単のためにそのままにしておいた)レイノルズ数が指数関数の肩にのっているので、レイノルズ数が大きくなるほど値が急激に変化することがわかる。
はレイノルズ数である。(本当はuの絶対値を取るのが正しいと思われるがここでは簡単のためにそのままにしておいた)レイノルズ数が指数関数の肩にのっているので、レイノルズ数が大きくなるほど値が急激に変化することがわかる。
境界での値を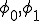 とすると解は次のようにかける。
とすると解は次のようにかける。
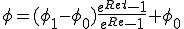
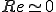 の場合
の場合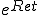 をテーラー展開して、
をテーラー展開して、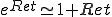 であるから、
であるから、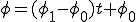 となる。つまり解は線形。
となる。つまり解は線形。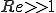 の場合
の場合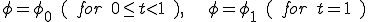 となる。
となる。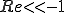 の場合
の場合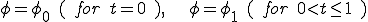 となる。
となる。
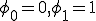 のとき、これらを図にすると次のとおり
のとき、これらを図にすると次のとおり
| レイノルズ数を変えたときの1次元定常移流拡散方程式の解の変化 |
|---|
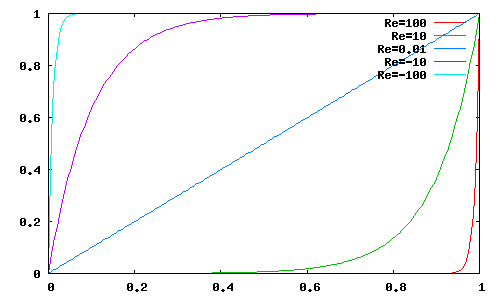 |
これを表示させるたgnuplotのコマンドは以下のとおり
set sample 100 set xrange [0:1] plot (exp(100*x)-1)/(exp(100)-1) title 'Re=100',(exp(10*x)-1)/(exp(10)-1) title 'Re=10', (exp(0.01*x)-1)/(exp(0.01)-1) title 'Re=0.01', (exp(-10*x)-1)/(exp(-10)-1) title 'Re=-10',(exp(-100*x)-1)/(exp(-100)-1) title 'Re=-100'
移流拡散方程式の解が基本的には指数関数であることが分かった。数値計算を行う場合は解の一次微分や2次微分を計算するためにさまざまな計算方法がある。一次微分を計算する際によく使われる中央差分では2次までの精度であるからこのような指数関数的な解には対応できない。そこで、移流項の部分で風上差分を用いた離散化がよく使われる.
| 一次風上差分法 |
|---|
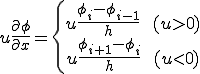 |
一次の風上差分は勾配を計算したい点x_iに対して1/2hだけ上流にある点における勾配を点x_iでの勾配とすることを意味している.
定常移流拡散方程式は風下に行くにしたがって解の勾配が大きくなることがわかる。
下の図は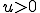 つまり左から右へ風が吹いてる時の解の様子である。
つまり左から右へ風が吹いてる時の解の様子である。
| 中央差分と風上差分の比較 |
|---|
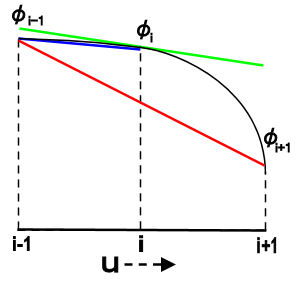 |
| 赤色の線の勾配は点iにおける中央差分を、 青色の線の勾配は点iにおける風上差分を、 緑色の線の勾配は点iにおける実際の勾配を表す |
上の図からも明らかなように、風上差分法は実際より小さめに、中央差分は実際より多きめに勾配の大きさが評価されることがわかる。
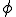 は直線であるから、中央差分と風上差分は実際の勾配に等しくなる。
は直線であるから、中央差分と風上差分は実際の勾配に等しくなる。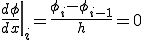 となり風上差分は実際の解と一致する。しかし風下の固定境界条件付近ではずれた大きな値をとってしまう。2回微分の項がそれと釣り合わなければならないのでここの部分で大きく凸や凹なりそれが風上に伝わって風下の固定境界付近で解が振動する。
となり風上差分は実際の解と一致する。しかし風下の固定境界条件付近ではずれた大きな値をとってしまう。2回微分の項がそれと釣り合わなければならないのでここの部分で大きく凸や凹なりそれが風上に伝わって風下の固定境界付近で解が振動する。上式は中央差分を用いて
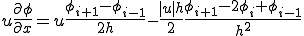
と変形できる.上式右辺第2項は風上差分を用いることによって人工的に導入された拡散項であるので人工拡散(Artificial Diffusion)または数値粘性と呼ぶ.また,人工拡散の係数を人工拡散係数と呼ぶ.
上式のように風上差分法による人工拡散係数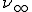 は
は
| 風上差分法による人工拡散係数 |
|---|
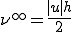 |
であたえられる.これらを用いると人工粘性を導入した移流拡散方程式は中央差分を用いることによって次のように書ける.
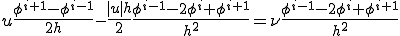
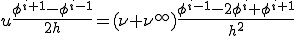
このとき風上差分はもともとの移流拡散方程式を
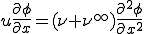
と書き換え中央差分したものと等しい.
移流項の影響が大きい場合は上式は精度よく厳密解と一致することが知られているが移流の影響が小さい場合に,実際の解と比べて数値解がなまされることが知られている.そこで移流の影響に応じて人工粘性の影響を変化させることで,数値解を厳密解と一致させることができる.
具体的には人工粘性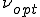 を以下のように定めればよい
を以下のように定めればよい
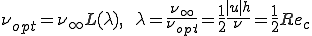
ここで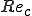 はセルレイノルズ数であり,
はセルレイノルズ数であり,
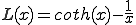
はランジュバン関数である.
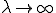 で
で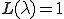 であるから,このとき
であるから,このとき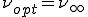 となる.すなわち,移流項の大きな問題に対して1次風上差分法の解は厳密解に一致する.また,
となる.すなわち,移流項の大きな問題に対して1次風上差分法の解は厳密解に一致する.また,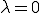 で
で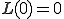 であるから移流項の影響が小さい場合は人工粘性の値も小さくなることが分かる.しかし,たとえ移流項の影響が小さくても人工粘性を加えた解のほうが厳密解に近くなることは注意が必要である.
であるから移流項の影響が小さい場合は人工粘性の値も小さくなることが分かる.しかし,たとえ移流項の影響が小さくても人工粘性を加えた解のほうが厳密解に近くなることは注意が必要である.
以上のことから,
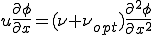
を中央差分で離散化すると厳密解を得ることができる.
1次元移流拡散問題にたいして,Bubnov-Galerkin法による有限要素法と中央差分による差分法が等しいことを示す.Bubnov-Galerkin法とは補間関数の形状関数と重み関数が等しいことをいう.
微分方程式
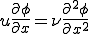
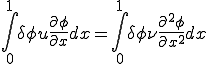
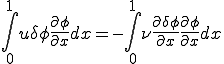
Bubnov-Galerkin法により形状関数と重み関数が互いに等しい関数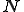 であらわされているとする.つまり,
であらわされているとする.つまり,
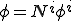 、
、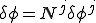
のように補間されているとする.上式を上式に代入すると
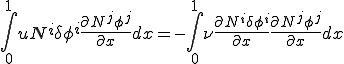
両辺から節点iでの重みの値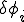 を削除すると
を削除すると
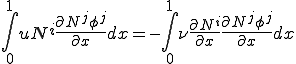
重み関数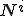 が0でない値を持つのは
が0でない値を持つのは![x=[x_i-h,x_i+h] x=[x_i-h,x_i+h]](46454D20666F7220416476656374696F6E2D446966667573696F6E204571756174696F6E_eq0058.gif) の範囲である.この範囲で形状関数
の範囲である.この範囲で形状関数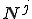 が0でない値を持つのは
が0でない値を持つのは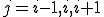 の時のみである.よって重み関数
の時のみである.よって重み関数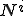 についての以下の式が成り立つ.
についての以下の式が成り立つ.
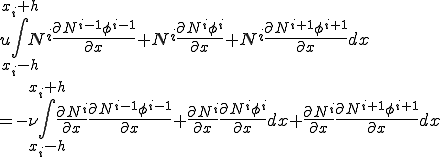
この積分を実行すると以下の式が得られる.
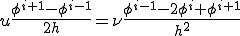
これは中央差分法を用いてこの問題を離散化した式と同一である.よってBubnov-Galerkin法と中央差分法は1次元の定常移流拡散問題では同一になることが分かる.
中央差分の場合は適切な人工粘性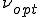 を導入することで数値解を厳密解にすることができることがわかった.そこで有限要素法の場合でも人工粘性
を導入することで数値解を厳密解にすることができることがわかった.そこで有限要素法の場合でも人工粘性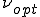 を付加することによって数値解を厳密解にすることができると考えられる.
を付加することによって数値解を厳密解にすることができると考えられる.
人工粘性を付加した弱形式は次のとおり
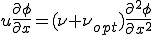
上式を参考にしてこの方程式の有限要素法による離散化は
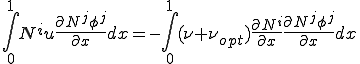
となる.この式を変形して人工粘性の項を左辺の移流項に移動させると
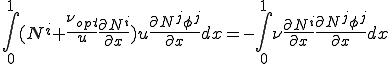
となる.この式の意味することは,上式の左辺つまり弱形式の移流項に対して重み関数を
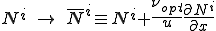
のように変形させたことに等しい.この形状関数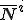 はもともとの形状関数
はもともとの形状関数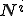 に比べて風上側の重みが大きく,風下側の重みが小さくなっており,風上差分と同じ効果をもっていることが分かる.
に比べて風上側の重みが大きく,風下側の重みが小さくなっており,風上差分と同じ効果をもっていることが分かる.
多次元における定常移流拡散方程式は次のようにかける.
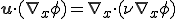
定常1次元移流拡散方程式の場合は粘性項に数値粘性係数を付加し,Bubnov-Galerkin法による離散化を行うことで解を精度よく求めることができた.しかし上式の粘性項に数値粘性係数をそのまま付加した式
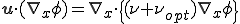
をBubnov-Galerkin法によって離散化するとなまった非現実的な解を与えることが知られている.風上差分のもともとの考えは風上方向に移流項の計算点を移動させることで流線方向に数値拡散を加えるというものだった.しかし,上式は粘性をただ大きくしただけで,流線方向に数値拡散を加えるだけではなく,流線方向に垂直な方向に対しても数値拡散を加えているので実際よりも粘性が大きくなってしまうので問題である.
そこで流線方向にのみ数値拡散項を付加することを考える.そのための準備として次のような流線方向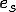 の空間微分オペレータを考える.
の空間微分オペレータを考える.
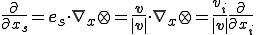
このオペレータを用いると例えば,
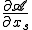
は流線方向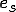 に沿った物理量
に沿った物理量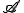 の単位長さあたりの変化量であり,流線方向の勾配(gradient)である.
の単位長さあたりの変化量であり,流線方向の勾配(gradient)である.
上式であらわされる多次元の定常移流拡散方程式に流線方向の人工粘性係数を付け加えた式は次のように書ける
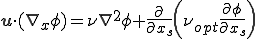
![{\b{u}}\cdot(\nabla_x\phi) = \nu \nabla^2 \phi + {\b{e}_s} \cdot \[ \nabla_x \{\nu_{opt}{\b{e}_s}\cdot (\nabla_x\phi)\}\] {\b{u}}\cdot(\nabla_x\phi) = \nu \nabla^2 \phi + {\b{e}_s} \cdot \[ \nabla_x \{\nu_{opt}{\b{e}_s}\cdot (\nabla_x\phi)\}\]](46454D20666F7220416476656374696F6E2D446966667573696F6E204571756174696F6E_eq0080.gif)
上式を弱形式化すると
![\int_v {\delta\phi}{\b{u}}\cdot(\nabla_x\phi) dv = -\int_v \nu \nabla_x{\delta\phi} \cdot \nabla_x\phi + {\delta\phi}{\b{e}_s} \cdot \[ \nabla_x\{\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\}\] dv \int_v {\delta\phi}{\b{u}}\cdot(\nabla_x\phi) dv = -\int_v \nu \nabla_x{\delta\phi} \cdot \nabla_x\phi + {\delta\phi}{\b{e}_s} \cdot \[ \nabla_x\{\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\}\] dv](46454D20666F7220416476656374696F6E2D446966667573696F6E204571756174696F6E_eq0081.gif)
右辺第3項について変形を行う.
![\int_v \delta\phi{\b{e}_s} \cdot \[ \nabla_x\{\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\}\] dv\\ = \int_v {\b{e}_s} \cdot \[ \nabla_x \{ \nu_{opt}{\delta\phi}{\b{e}_s}\cdot(\nabla_x\phi)\} \] - \{{\b{e}_s}\cdot(\nabla_x{\delta\phi})\} \{\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\} dv\\ = \int_v \nabla_x \cdot [ \{{\delta\phi}\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\} {\b{e}_s}\] - \underbrace{\left\{\nabla_x \cdot {\b{e}_s}\right\}}_{=0} \{{\delta\phi}\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\} - \{{\b{e}_s}\cdot(\nabla_x{\delta\phi})\} \{\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\} dv \int_v \delta\phi{\b{e}_s} \cdot \[ \nabla_x\{\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\}\] dv\\ = \int_v {\b{e}_s} \cdot \[ \nabla_x \{ \nu_{opt}{\delta\phi}{\b{e}_s}\cdot(\nabla_x\phi)\} \] - \{{\b{e}_s}\cdot(\nabla_x{\delta\phi})\} \{\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\} dv\\ = \int_v \nabla_x \cdot [ \{{\delta\phi}\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\} {\b{e}_s}\] - \underbrace{\left\{\nabla_x \cdot {\b{e}_s}\right\}}_{=0} \{{\delta\phi}\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\} - \{{\b{e}_s}\cdot(\nabla_x{\delta\phi})\} \{\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\} dv](46454D20666F7220416476656374696F6E2D446966667573696F6E204571756174696F6E_eq0082.gif)
第1項についてガウスの発散定理を適応する.また,流線方向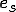 は一定とすると,第2項は0となる.よって上式は
は一定とすると,第2項は0となる.よって上式は
![\int_s{\b{n}}\cdot\underbrace{\[ \{{\delta\phi}\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\}{\b{e}_s} \]}_{=0}ds - \int_v\{{\b{e}_s}\cdot(\nabla_x{\delta\phi})\}\{{\nu_{opt}}{\b{e}_s}\cdot(\nabla_x\phi)\} dv\\ = -\int_v\{{\b{e}_s}\cdot(\nabla_x{\delta\phi})\} \{{\nu_{opt}}{\b{e}_s}\cdot(\nabla_x\phi)\} dv\\ = -\int_v\{\frac{\b{v}}{|\b{v}|}\cdot(\nabla_x{\delta\phi})\} \{{\nu_{opt}}\frac{\b{v}}{|\b{v}|}\cdot(\nabla_x\phi)\} dv\\ = -\int_v\{\frac{\nu_{opt}}{|\b{v}|^2}{\b{v}}\cdot(\nabla_x{\delta\phi})\} \{{\b{v}}\cdot(\nabla_x\phi)\} dv \int_s{\b{n}}\cdot\underbrace{\[ \{{\delta\phi}\nu_{opt}{\b{e}_s}\cdot(\nabla_x\phi)\}{\b{e}_s} \]}_{=0}ds - \int_v\{{\b{e}_s}\cdot(\nabla_x{\delta\phi})\}\{{\nu_{opt}}{\b{e}_s}\cdot(\nabla_x\phi)\} dv\\ = -\int_v\{{\b{e}_s}\cdot(\nabla_x{\delta\phi})\} \{{\nu_{opt}}{\b{e}_s}\cdot(\nabla_x\phi)\} dv\\ = -\int_v\{\frac{\b{v}}{|\b{v}|}\cdot(\nabla_x{\delta\phi})\} \{{\nu_{opt}}\frac{\b{v}}{|\b{v}|}\cdot(\nabla_x\phi)\} dv\\ = -\int_v\{\frac{\nu_{opt}}{|\b{v}|^2}{\b{v}}\cdot(\nabla_x{\delta\phi})\} \{{\b{v}}\cdot(\nabla_x\phi)\} dv](46454D20666F7220416476656374696F6E2D446966667573696F6E204571756174696F6E_eq0084.gif)
と式変形される.これを上式に代入すると
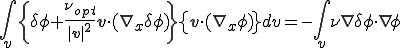
これは移流項の重み関数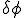 を
を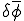 と変化させることに等しい.
と変化させることに等しい.
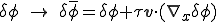
但し,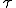 は以下で定義される安定化パラメータである.
は以下で定義される安定化パラメータである.
| 安定化パラメータ |
|---|
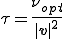 |
ここで付加した数値拡散について詳しく調べる.数値拡散の項を変形すると,
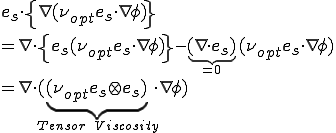
流線の方向の変化は無視できるとした.ここで
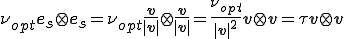
はテンソル粘性(Tensor Viscosity)という.流線の方向にのみ粘性となる値が存在するような異方性を有していることがわかる.
安定化パラメータは次のように表されるのであった。
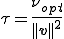
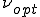 は次のようにすると、一次元において節点における解が厳密解と一致するのであった。
は次のようにすると、一次元において節点における解が厳密解と一致するのであった。
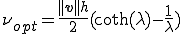 、
、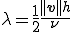
ここで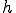 はメッシュサイズである。1次元の場合はメッシュサイズは線要素の長さと等しいので特に問題ないのであるが、2次元3次元の場合はメッシュサイズは簡単には決まらない。2次元や3次元の要素では
はメッシュサイズである。1次元の場合はメッシュサイズは線要素の長さと等しいので特に問題ないのであるが、2次元3次元の場合はメッシュサイズは簡単には決まらない。2次元や3次元の要素では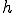 は流速の方向についての要素の長さを代表していなければならない。
は流速の方向についての要素の長さを代表していなければならない。
Tezduyarは1991年の論文*1の中で次の様に流速方向のメッシュサイズを決定している。
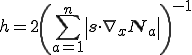
ここで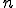 は要素の内挿関数の数である。また
は要素の内挿関数の数である。また は流速ベクトル
は流速ベクトル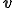 を長さが1に規格化した方向ベクトルである。
を長さが1に規格化した方向ベクトルである。
また、この論文では次のような近似を用いている。
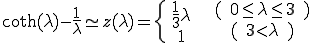
近似関数zと近似される前の関数は次のグラフのとおり
次のサンプルプログラムは大きさ1×1の矩形領域における次のような移流拡散方程式(Advection Diffusion Problem)を解く問題である。
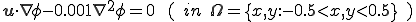
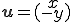
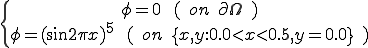
矩形領域に原点を通る切り込みが入っており、そこに固定境界条件がはいっている。流速は原点を中心に円を描くように反時計周りで流れているものとする。
問題の離散化は安定化有限要素法を用いている。
| DOWNLOAD | GMRes.zip |
|---|
OS:WindowsXP, Windows2000 開発環境:VC++ 2005 言語:C++
プログラムを実行すると'solution.dat'という結果ファイルが生成される。
'solution.dat'はgnuplot用のデータ形式をしている
windows版のgnuplotの導入は以下のページが詳しい
gnuplotを起動した後、プログラムを実行した'solution.dat'のあるディレクトリに移動し、次のようなコマンドを打つと結果が表示される。
gnuplot> set style data line gnuplot> splot 'solution.dat'
また次のようなコマンドを打つとgnuplotは下のような等高線を表示する。
gnuplot> set nosurface gnuplot> set contour base gnuplot> set view 180,90 gnuplot> splot 'solution.dat'
| 有限要素法による流れのシミュレーション | 日本数値流体力学学会有限要素法研究委員会 (著) |
| 流れの有限要素法解析(2) | 棚橋 隆彦 (著), 伊理 正夫 (著), 三好 俊郎 (著), 小国 力 (著), 小柳 義夫 (著) |