![f\in L^2[a,b] f\in L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0001.gif) について積分演算子
について積分演算子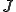 を次のように定義する。
を次のように定義する。|TOP Page|
いきなり多次元の問題にすると、イメージを掴みにくい。とりあえず、1次元の問題について考える。
![f\in L^2[a,b] f\in L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0001.gif) について積分演算子
について積分演算子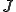 を次のように定義する。
を次のように定義する。
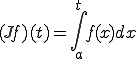
ここで、ルーベルグ積分の定義から、
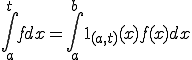
と置けることに注意しよう。
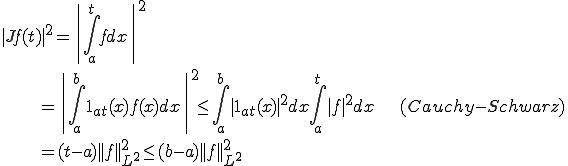
これを用いると、
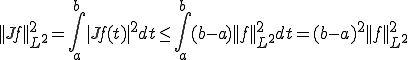
つまり、
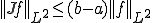
が成り立つ。よって積分演算子は有界□
![f\in L^2[a,b] f\in L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0008.gif) として、
として、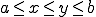 とすると、
とすると、
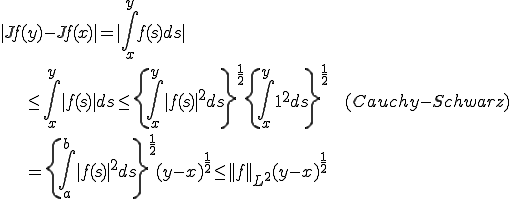
よって![L^2[a,b] L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0011.gif) を積分した関数は
を積分した関数は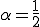 のHolder連続である。
のHolder連続である。
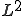 空間は連続関数を
空間は連続関数を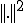 ノルムで完備化したものである。それゆえに一般的に微分可能とは限らない。ここで、微分の概念を一般化した、弱微分を導入する。
ノルムで完備化したものである。それゆえに一般的に微分可能とは限らない。ここで、微分の概念を一般化した、弱微分を導入する。
![f\in L^2[a,b] f\in L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0015.gif) に関して、
に関して、
![\int_a^b f'\psi dx=-\int_a^b f\psi'dx\quad\quad\forall\psi\in C_0^1[a,b] \int_a^b f'\psi dx=-\int_a^b f\psi'dx\quad\quad\forall\psi\in C_0^1[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0016.gif)
が成り立つ場合、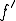 は
は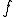 の弱微分と呼ばれる。
の弱微分と呼ばれる。
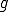 が連続関数であるとする。このとき、積分はリーマン積分となるので、
が連続関数であるとする。このとき、積分はリーマン積分となるので、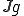 の(弱微分ではない)微分が可能であり、
の(弱微分ではない)微分が可能であり、
![(Jg)'=g\in C[a,b] (Jg)'=g\in C[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0021.gif)
となる。微分が連続であるから![g\in C^1[a,b] g\in C^1[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0022.gif) であることが分かる。
であることが分かる。
よって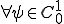 について
について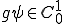
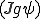 の微分のリーマン積分が可能であり、
の微分のリーマン積分が可能であり、
![\int_a^b\{Jg\psi\}'dx=\[Jg\psi\]_a^b=0\\\quad\quad=\int_a^b (Jg)'\psi dx+\int_a^b (Jg)\psi' dx \int_a^b\{Jg\psi\}'dx=\[Jg\psi\]_a^b=0\\\quad\quad=\int_a^b (Jg)'\psi dx+\int_a^b (Jg)\psi' dx](6261736973206F6620536F626F6C6576205370616365_eq0026.gif)
よって、
![\int_a^b g\psi dx=-\int_a^b (Jg)\psi' dx\qquad\qquad\forall \psi\in C^1_0[a,b] \int_a^b g\psi dx=-\int_a^b (Jg)\psi' dx\qquad\qquad\forall \psi\in C^1_0[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0027.gif)
が成り立つ。よって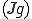 の弱微分もまた
の弱微分もまた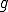 である。□
である。□
![f\in L^2[a,b] f\in L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0030.gif) について、弱微分を用いて
について、弱微分を用いて
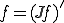
となる。
![L^2[a,b] L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0032.gif) 空間は
空間は![C[a,b] C[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0033.gif) を
を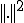 ノルムについて完備化したものだった。
ノルムについて完備化したものだった。
![f\in C[a,b] f\in C[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0035.gif) については、前の証明より弱微分と強い微分は等しい。そこで積分作用素
については、前の証明より弱微分と強い微分は等しい。そこで積分作用素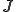 の連続性と
の連続性と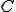 が
が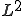 で稠密であることを用いて、これを
で稠密であることを用いて、これを![f\in L^2[a,b] f\in L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0039.gif) について拡張する。
について拡張する。
![f_n\in C[a,b] f_n\in C[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0040.gif) をノルム
をノルム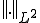 における任意のCauchy列であるとする。
における任意のCauchy列であるとする。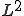 空間は
空間は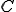 空間を完備化したものだったから、
空間を完備化したものだったから、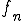 は
は![L^2[a,b] L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0045.gif) 内に極限
内に極限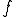 を持つ
を持つ
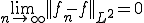
積分演算子の有界性から、
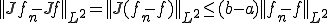
よって
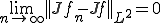
となる。
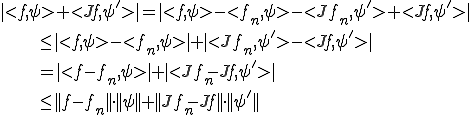
よって
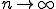 とすると、
とすると、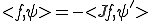 が成り立つ。
が成り立つ。
つまり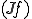 の弱微分は
の弱微分は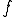 である。□
である。□
弱微分が0であるから、
![\int_a^b f\psi' ds=0\quad\forall \psi\in C^1_0[a,b] \int_a^b f\psi' ds=0\quad\forall \psi\in C^1_0[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0055.gif)
が成り立つ。よって、上が成り立つような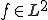 は定数であることを示せばよい。
は定数であることを示せばよい。
まず、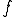 が次のような定数
が次のような定数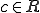 であると予測を立てる。
であると予測を立てる。
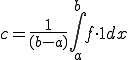
この定数 は
は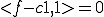 が成り立つ
が成り立つ
題意を満たすためには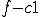 が0であることを示せばよい。証明の方針としては、
が0であることを示せばよい。証明の方針としては、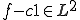 が任意の連続関数と直交することを示した後、連続関数の空間が
が任意の連続関数と直交することを示した後、連続関数の空間が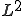 関数の空間で稠密であることを利用して、任意の
関数の空間で稠密であることを利用して、任意の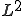 関数と直交することを示す。全ての
関数と直交することを示す。全ての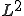 関数と直交する
関数と直交する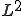 関数は0である。ので
関数は0である。ので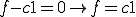 がいえる。
がいえる。
さて、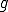 を任意の連続関数としよう。この時、
を任意の連続関数としよう。この時、
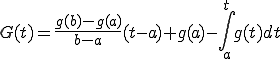
は![C^1_0[a,b] C^1_0[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0071.gif) 関数であり、その微分は
関数であり、その微分は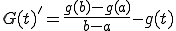 である。
である。
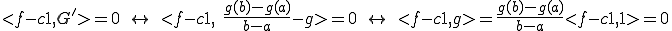
よって任意の連続関数と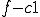 は直交することがわかる。
は直交することがわかる。
さて、連続関数は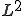 空間の中で稠密であったから、任意の
空間の中で稠密であったから、任意の![h\in L^2[a,b] h\in L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0076.gif) に対して、
に対して、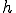 に収束する連続関数のCauchy列
に収束する連続関数のCauchy列![h_n\in C[a,b] h_n\in C[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0078.gif) が存在する。
が存在する。
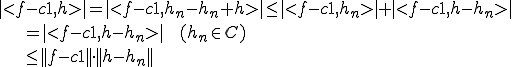
よって右辺はいくらでも小さくできるので、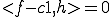 が成り立つ。
が成り立つ。
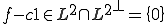
よって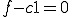 が成り立つ。つまり、
が成り立つ。つまり、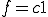 、
、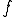 は定数である。□
は定数である。□
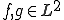 の弱微分
の弱微分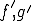 が存在して、それらが
が存在して、それらが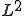 空間に含まれるとする。このとき、
空間に含まれるとする。このとき、
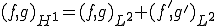
で定義されるような内積を持つような空間をソボレフ空間という。
ソボレフ空間の任意の要素![g\in H^1[a,b] g\in H^1[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0089.gif) は次のように定数
は次のように定数 と
と![f\in L^2[a,b] f\in L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0091.gif) を使って次のように書くことができる。
を使って次のように書くことができる。
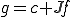
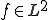 とすると
とすると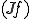 の弱微分は
の弱微分は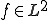 であるから、
であるから、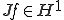 である。
である。
これを用いて、任意の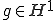 について、
について、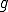 の弱微分
の弱微分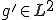 であるから、
であるから、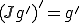 が成り立つ。
が成り立つ。
つまり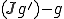 の弱微分は0。
の弱微分は0。
前の問題より、弱微分が0ならば、定数であった。よってある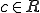 が存在して、
が存在して、
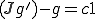
となる。つまり任意の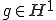 は、実数
は、実数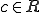 と
と![f\in L^2[a,b] f\in L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0106.gif) を用いて
を用いて
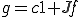
のように表すことができる。□
![L^2[a,b] L^2[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0108.gif) 関数を積分したものは
関数を積分したものは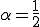 のHöler連続であったから、ソボレフ空間の任意の要素もまた
のHöler連続であったから、ソボレフ空間の任意の要素もまた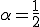 のHöler連続である。
のHöler連続である。
![C^1[a,b] C^1[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0111.gif) 空間が
空間が![H^1[a,b] H^1[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0112.gif) 空間の中で稠密であることを示そう。
空間の中で稠密であることを示そう。
任意の関数![g\in H^1[a,b] g\in H^1[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0113.gif) について、それに収束する関数のCauchy列
について、それに収束する関数のCauchy列![g_n\in C^1[a,b] g_n\in C^1[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0114.gif) があればいい。
があればいい。
さて、任意の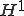 の関数
の関数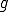 は
は
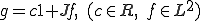
のように表すことができた。但し、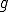 の弱微分
の弱微分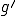 とすると、
とすると、
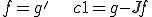
ここで、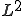 空間は
空間は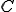 空間を完備化したものだから、
空間を完備化したものだから、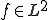 に対して,ある連続関数の
に対して,ある連続関数の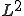 ノルムに関するCauchy列
ノルムに関するCauchy列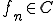 が存在して
が存在して
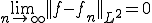
となる。ここで、次のような関数列![g_n\in C^1[a,b] g_n\in C^1[a,b]](6261736973206F6620536F626F6C6576205370616365_eq0127.gif) を考える
を考える
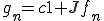
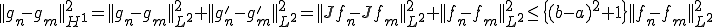
よって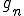 もCauchy列である。さて、
もCauchy列である。さて、
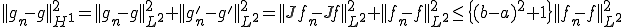
よって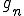 は
は 空間で
空間で に収束する。任意の
に収束する。任意の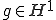 に対して、収束するようなCauchy列
に対して、収束するようなCauchy列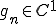 が存在するので、
が存在するので、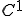 空間は
空間は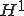 空間で稠密であるといえる。□
空間で稠密であるといえる。□
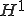 空間内の関数で境界で0となるような値を取る関数が作る部分空間を
空間内の関数で境界で0となるような値を取る関数が作る部分空間を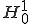 とかく。このとき
とかく。このとき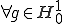 に対して、弱微分を
に対して、弱微分を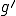 のように表すと、
のように表すと、
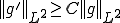
が成り立つ。ここで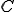 は領域の大きさ
は領域の大きさ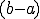 にのみ依存するパラメータ
にのみ依存するパラメータ
任意の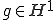 に対して、
に対して、
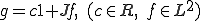
と表すことができた。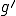 を弱微分であるとすると、
を弱微分であるとすると、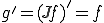 となる。
となる。
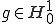 のとき
のとき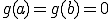 である。これから、
である。これから、
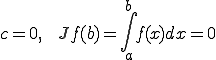
がいえる。よって、
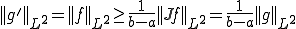
が成り立つ。また、このとき、
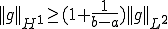
も成り立つ。□
次のような方程式を解くとする。
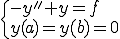
このままでは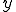 には2階微分が可能であることが要求され、右辺
には2階微分が可能であることが要求され、右辺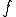 によっては解が存在しない場合がある。
によっては解が存在しない場合がある。
さて、上の方程式を直接解く代わりに、次のような方程式を解くことを考える。
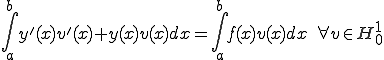
但し、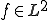 、
、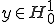 であるとし、
であるとし、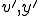 は
は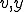 の弱い微分であるとした。右辺がソボレフ空間の内積になっていることに注意されたい。
の弱い微分であるとした。右辺がソボレフ空間の内積になっていることに注意されたい。
ここで、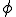 は次で定義される
は次で定義される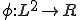 の線形関数であるとする。
の線形関数であるとする。
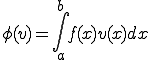
これを用いて書き換えると
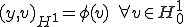
のようになる。
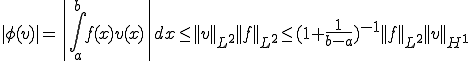
であるから は
は 空間で有界関数である。よってReiezの定理より解
空間で有界関数である。よってReiezの定理より解 が存在して唯一定まる。
が存在して唯一定まる。
距離空間、ノルム、線形写像、直和、零空間、作用素、ヒルベルト空間、完備、バナッハ空間
| Functional Analysis | Kosaku Yosida 著 |
| Functional Analysis in Applied Mathematics and Engineering | Michael Pedersen 著 |
| ヒルベルト空間論 | 保江邦夫 著 |