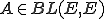 に対して、次の(I)(II)の性質を持つ
に対して、次の(I)(II)の性質を持つ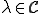 の集合をレゾルベント集合といい、
の集合をレゾルベント集合といい、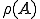 と表す。
と表す。(I)
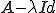 が可逆
が可逆(II)
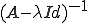 が有界
が有界|TOP Page|
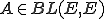 に対して、次の(I)(II)の性質を持つ
に対して、次の(I)(II)の性質を持つ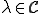 の集合をレゾルベント集合といい、
の集合をレゾルベント集合といい、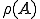 と表す。
と表す。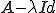 が可逆
が可逆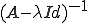 が有界
が有界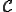 のうちレゾルベント集合に入らないものをスペクトルといい、
のうちレゾルベント集合に入らないものをスペクトルといい、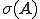 と表す。
と表す。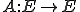 について、次のような、
について、次のような、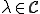 と
と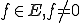 が存在するとき、
が存在するとき、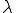 は
は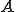 の固有値と呼ばれる
の固有値と呼ばれる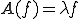
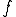 は固有ベクトル、固有関数などと呼ばれる。
は固有ベクトル、固有関数などと呼ばれる。
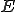 がノルム空間とし、作用素
がノルム空間とし、作用素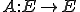 が線形であるとすると、全ての固有値はスペクトル
が線形であるとすると、全ての固有値はスペクトル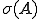 に含まれる。
に含まれる。
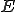 が有限次元ノルム空間であり、作用素
が有限次元ノルム空間であり、作用素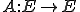 が線形だとすると、スペクトル
が線形だとすると、スペクトル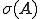 と固有値の集合は等しい。
と固有値の集合は等しい。
 がバナッハ空間であり、
がバナッハ空間であり、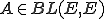 であるとする。
であるとする。
レゾンベルト集合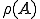 が開空間であることを示す。
が開空間であることを示す。
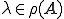 として、全ての
として、全ての
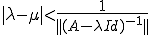
を満たす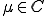 は、
は、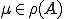 であることを示す。
であることを示す。
バナッハ空間においては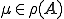 であるためには、
であるためには、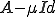 が可逆であることを示せばよい。
が可逆であることを示せばよい。
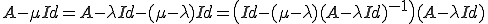
ここで、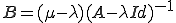 とおく。
とおく。
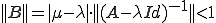
よって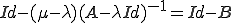 は可逆。
は可逆。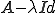 は可逆であったから、
は可逆であったから、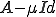 も可逆であり、
も可逆であり、
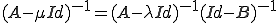
が成り立つ。よって補空間が開空間であるからスペクトルは閉空間である。□
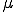 がスペクトルなら、
がスペクトルなら、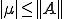 であることを示すためには
であることを示すためには
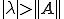 ならば
ならば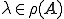 であることを示せばよい。つまり
であることを示せばよい。つまり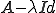 が可逆であることを示せばよい。
が可逆であることを示せばよい。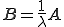 とおくと、
とおくと、
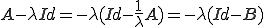
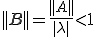 より
より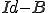 は可逆である。よって
は可逆である。よって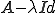 は可逆で
は可逆で
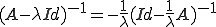
となる。以上から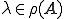 となり、題意は証明された。□
となり、題意は証明された。□
もし、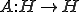 が自己共役ならば、
が自己共役ならば、
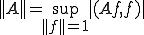
となる。
まず、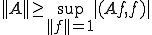 を示し、次に
を示し、次に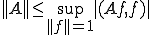 を示すことで証明する。
を示すことで証明する。
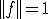 のとき、
のとき、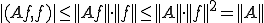
よって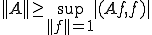 は明らか
は明らか
次に、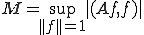 とおき、
とおき、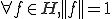 に対して
に対して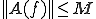 を示す。
を示す。
ここで、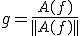 とおくと、
とおくと、
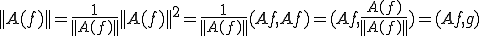
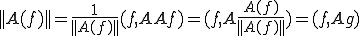
さて、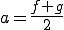 、
、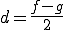 と置く。
と置く。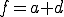 、
、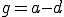 を上に代入して
を上に代入して
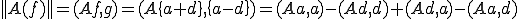
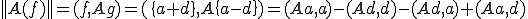
よって、上二式の和を計算して、
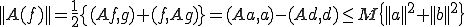
が成り立つ。中線定理より、
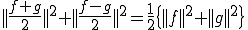
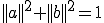
これを上に代入すると
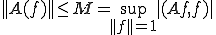
がいえる。
以上から
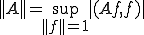
となる。□
 上の有界線形作用素
上の有界線形作用素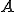 がなんらかの複素数
がなんらかの複素数 と規格化された点列
と規格化された点列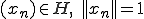 に対して
に対して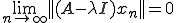
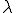 を
を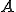 の近似固有値という
の近似固有値という
自己共役作用素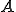 は
は か
か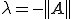 の近似固有値を持つ。
の近似固有値を持つ。
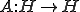 として、ある列
として、ある列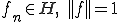 が存在して、
が存在して、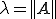 か
か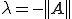 について、
について、
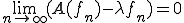
であることを示せばよい。
前の定理より、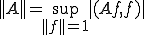 であったから、ある列
であったから、ある列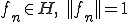 が存在して、
が存在して、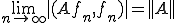 とすることができる。
とすることができる。
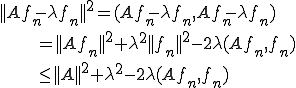
ここで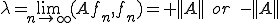 とおけば、右辺は幾らでも小さくできるので
とおけば、右辺は幾らでも小さくできるので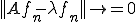 となる。
となる。
よって題意は証明された□
完全連続な自己共役作用素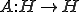 は
は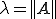 か
か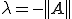 の固有値を持つ。
の固有値を持つ。
前の定理から自己共役作用素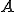 は
は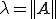 か
か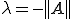 の近似固有値を持つことが分かる。つまり、ある
の近似固有値を持つことが分かる。つまり、ある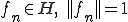 が存在して、
が存在して、
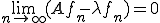
となる。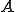 が完全連続作用素であるので、前の定理より
が完全連続作用素であるので、前の定理より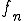 は
は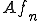 が収束する部分列
が収束する部分列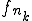 を含んでいる。さて、ここで
を含んでいる。さて、ここで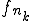 を
を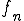 となるように選びなおす。また、
となるように選びなおす。また、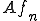 が
が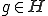 に収束するとする。
に収束するとする。
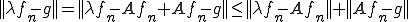
であるから
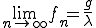
となる。
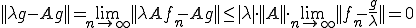
よって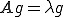 となることから、
となることから、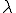 は固有値となる。□
は固有値となる。□
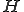 をヒルベルト空間として、
をヒルベルト空間として、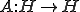 を完全連続な自己共役作用素とする。この時、次のような、1次元部分空間への正射影演算子と実数が存在する。
を完全連続な自己共役作用素とする。この時、次のような、1次元部分空間への正射影演算子と実数が存在する。
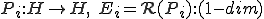
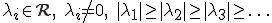
ここで、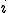 は有限な場合も無限な場合もある。つまり
は有限な場合も無限な場合もある。つまり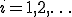 か
か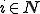 である。
である。
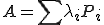
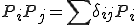
が成り立つ。さらに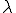 が無限に存在する場合は
が無限に存在する場合は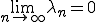 となる。
となる。
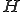 をヒルベルト空間として、
をヒルベルト空間として、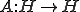 を完全連続な自己共役作用素とすると、固有値
を完全連続な自己共役作用素とすると、固有値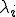 と正規完全直交系
と正規完全直交系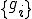 が存在して
が存在して
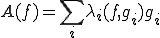
となる。さらに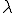 が無限に存在する場合は
が無限に存在する場合は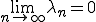 となる。
となる。
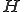 をヒルベルト空間として、
をヒルベルト空間として、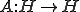 を完全連続な自己共役作用素とする。次のような、
を完全連続な自己共役作用素とする。次のような、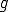 を固定して
を固定して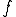 を求めるような方程式を考える
を求めるような方程式を考える
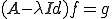
(a)もし、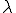 が
が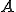 の固有値でないなら、全ての
の固有値でないなら、全ての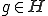 に対して唯一の解
に対して唯一の解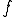 が存在して、次のように与えられる。
が存在して、次のように与えられる。
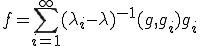
但し、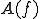 は、最大正規直交系
は、最大正規直交系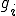 を使って、次のように与えられる。
を使って、次のように与えられる。
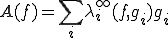
また、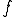 は
は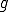 に対して連続に与えられる。
に対して連続に与えられる。
(b)もし、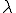 が
が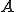 の固有値なら、
の固有値なら、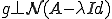 の場合に限り、解
の場合に限り、解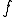 は次のように与えられる。
は次のように与えられる。
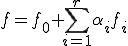
ここで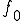 は任意の解で、
は任意の解で、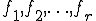 は固有値
は固有値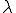 に対応する固有値空間
に対応する固有値空間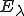 の基底である。
の基底である。
距離空間、ノルム、線形写像、直和、零空間、作用素、ヒルベルト空間、完備、バナッハ空間
| Functional Analysis | Kosaku Yosida 著 |
| Functional Analysis in Applied Mathematics and Engineering | Michael Pedersen 著 |
| ヒルベルト空間論 | 保江邦夫 著 |