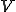 を線形空間として、
を線形空間として、|TOP Page|
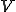 を線形空間として、
を線形空間として、
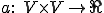
 正定値双線形関数、つまり
正定値双線形関数、つまり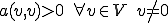 が成り立つとする。
が成り立つとする。
また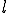 を線形関数とする
を線形関数とする
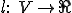
このとき次の関数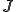 を次のように定める
を次のように定める
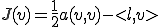
(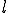 は関数なので
は関数なので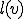 と書いてもよいのだが、線形性を強調するためにベクトル
と書いてもよいのだが、線形性を強調するためにベクトル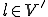 を用いて
を用いて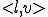 のように書く)
のように書く)
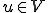 とすると、この関数
とすると、この関数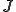 が
が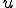 において最小値を取るための必要十分条件は次が成り立つことである。
において最小値を取るための必要十分条件は次が成り立つことである。
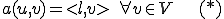
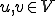 また
また 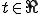 に対して以下が成り立つ。
に対して以下が成り立つ。
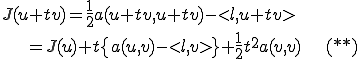
もしも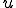 が(*)を満たす場合、第二項が0となる。ここでt=1とおくと(**)は次のようになる
が(*)を満たす場合、第二項が0となる。ここでt=1とおくと(**)は次のようになる
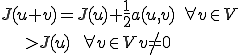
よって(*)が成り立てば、 は唯一
は唯一 において最小値をとることがわかる。
において最小値をとることがわかる。
反対に が
が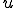 において最小値を取る場合、(**)のt=0における、tの微分が全ての
において最小値を取る場合、(**)のt=0における、tの微分が全ての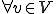 に対して0でなければならないから、
に対して0でなければならないから、
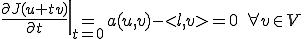
つまり(*)が成り立つ。
 を凸で閉じたHirbert空間とし、
を凸で閉じたHirbert空間とし、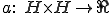 を楕円双線形関数とする。つまり
を楕円双線形関数とする。つまり は有界かつ
は有界かつ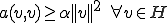 が成り立つとする。このとき任意の関数
が成り立つとする。このとき任意の関数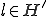 について次の変分問題は
について次の変分問題は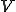 の中に解を唯一持つ
の中に解を唯一持つ
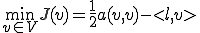
次のように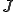 は下に有界である。
は下に有界である。
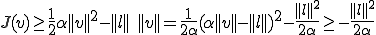
そこで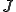 の下限を
の下限を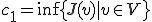 のように定める。また、
のように定める。また、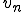 を
を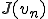 が単調減少するような
が単調減少するような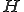 の中の数列であるとする。
の中の数列であるとする。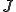 は下に有界であったから、
は下に有界であったから、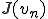 は
は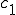 に収束する。つまりnを大きくすれば
に収束する。つまりnを大きくすれば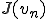 は
は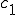 にいくらでも近づく
にいくらでも近づく
最後の変形では が凸であるから
が凸であるから であることを用いた。ここで
であることを用いた。ここで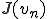 、
、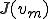 が
が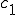 に収束するので、
に収束するので、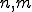 を大きくすれば、上式はいくらでも0に近づけることができる。
を大きくすれば、上式はいくらでも0に近づけることができる。
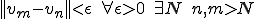
つまり はCauchy列である。よって
はCauchy列である。よって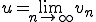 が存在し、
が存在し、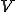 が閉空間であるから
が閉空間であるから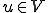 である。
である。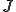 の有界性より、
の有界性より、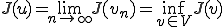 である。
である。
さて、Lax-Milgramの補題と特徴化定理により汎関数が最少となるような解の唯一存在性と解を与える方程式を導くことができた。次に実際の問題にこれを応用してみよう。
次のような2次楕円型の境界値問題を解くとする
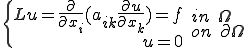
この場合に次の方程式の解は次の汎関数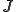
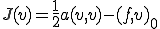
の境界上で0であり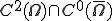 に含まれる全ての関数の中での最小値である。(但し
に含まれる全ての関数の中での最小値である。(但し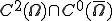 は領域の内側で2階微分可能で2階微分連続、かつ境界上で連続な関数の集合)但し、
は領域の内側で2階微分可能で2階微分連続、かつ境界上で連続な関数の集合)但し、
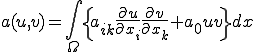
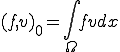
である。
ここで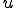 を上の楕円型の偏微分方程式の解とする。また
を上の楕円型の偏微分方程式の解とする。また は境界上で0となる任意の
は境界上で0となる任意の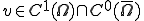 とする。
とする。
![a(u,v)-(f,v)_0=\int_{\Omega}\[ a_{ik}\frac{\partial v}{\partial x_i}\frac{\partial v}{\partial x_k}+a_0 uv-fv \]dx\\\qquad\qquad = \int_{\Omega}\[ \frac{\partial}{\partial x_i}(v a_{ik}\frac{\partial u}{\partial x_k})-v\frac{\partial}{\partial x_i}(a_{ik}\frac{\partial u}{\partial x_k})+a_0 uv-fv \]dx\\\qquad\qquad = \int_{\partial\Omega}n_i(v a_{ik}\frac{\partial u}{\partial x_k})ds+\int_{\Omega}v\[-\frac{\partial}{\partial x_i}(a_{ik}\frac{\partial u}{\partial x_k})+a_0 u-f\]dx\\\qquad\qquad\int_{\Omega}v\[Lu-f\]dx=0 a(u,v)-(f,v)_0=\int_{\Omega}\[ a_{ik}\frac{\partial v}{\partial x_i}\frac{\partial v}{\partial x_k}+a_0 uv-fv \]dx\\\qquad\qquad = \int_{\Omega}\[ \frac{\partial}{\partial x_i}(v a_{ik}\frac{\partial u}{\partial x_k})-v\frac{\partial}{\partial x_i}(a_{ik}\frac{\partial u}{\partial x_k})+a_0 uv-fv \]dx\\\qquad\qquad = \int_{\partial\Omega}n_i(v a_{ik}\frac{\partial u}{\partial x_k})ds+\int_{\Omega}v\[-\frac{\partial}{\partial x_i}(a_{ik}\frac{\partial u}{\partial x_k})+a_0 u-f\]dx\\\qquad\qquad\int_{\Omega}v\[Lu-f\]dx=0](4D617468656D61746963616C20626173697320666F722046454D_eq0071.gif)
が成り立つ。但し、2番目の式から3番目の式はGreen-Gaussの定理を用いた。従って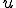 が解ならば境界上でv=0となる任意の
が解ならば境界上でv=0となる任意の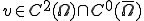 について(
について(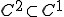 である)
である)
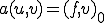
を満たす。よって特徴化定理より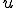 が解であることの必要十分条件は
が解であることの必要十分条件は
汎関数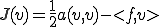 が
が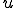 において全ての境界上で0となる
において全ての境界上で0となる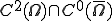 の関数の中での最小値をとることである。
の関数の中での最小値をとることである。
上で示した汎関数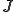
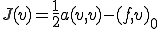
の最小値が上の楕円問題の解となるのは境界上で0となる の関数の中で
の関数の中で が最小値をとる場合である。残念ながら
が最小値をとる場合である。残念ながら では最小値となる解の唯一存在性に必要なaの楕円性を示すことはできない。その代わりに
では最小値となる解の唯一存在性に必要なaの楕円性を示すことはできない。その代わりに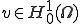 で上の汎関数の最小値の唯一存在性を示すことができる。
で上の汎関数の最小値の唯一存在性を示すことができる。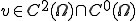 の中での最小値ではなくて
の中での最小値ではなくて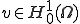 の中での最小値であるので解は2階微分ができてそれが連続という条件を満たさなくてもよく、より弱い1回微分が2乗可積分であるという条件を満たしさえすればよい。このような
の中での最小値であるので解は2階微分ができてそれが連続という条件を満たさなくてもよく、より弱い1回微分が2乗可積分であるという条件を満たしさえすればよい。このような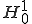 の中で汎関数を最少にするような解は解としての条件が弱いことから弱い解(weak solution)と呼ばれる
の中で汎関数を最少にするような解は解としての条件が弱いことから弱い解(weak solution)と呼ばれる
汎関数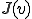 を
を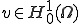 の範囲で最小化するような弱解は常に唯一存在し、次の方程式を満たす
の範囲で最小化するような弱解は常に唯一存在し、次の方程式を満たす
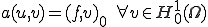
これを証明しよう。
 の
の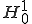 における有界性と楕円性をまずしめす。これを示すことができれば、Lax-Milgramの定理から解の唯一存在性がいえる。
における有界性と楕円性をまずしめす。これを示すことができれば、Lax-Milgramの定理から解の唯一存在性がいえる。
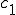 は係数
は係数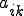 の上限とする。つまり
の上限とする。つまり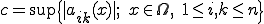 するとCauchy-Schwarzの定理より
するとCauchy-Schwarzの定理より
![\left|\sum_{i,k}\int a_{ik}\frac{\partial u}{\partial x_i}\frac{\partial v}{\partial x_k}dx\right|\le c_1\sum_{i,k}\int\left|\frac{\partial u}{\partial x_i}\frac{\partial u}{\partial x_k}\right|dx\\ \qquad\qquad\qquad\le c_1\sum_{i,k}\[\int(\frac{\partial u}{\partial x_i})^2dx\int(\frac{\partial u}{\partial x_k})^2dx\]^{1/2}\\ \qquad\qquad\qquad\le c_1n^2|u|_1|v|_1 \left|\sum_{i,k}\int a_{ik}\frac{\partial u}{\partial x_i}\frac{\partial v}{\partial x_k}dx\right|\le c_1\sum_{i,k}\int\left|\frac{\partial u}{\partial x_i}\frac{\partial u}{\partial x_k}\right|dx\\ \qquad\qquad\qquad\le c_1\sum_{i,k}\[\int(\frac{\partial u}{\partial x_i})^2dx\int(\frac{\partial u}{\partial x_k})^2dx\]^{1/2}\\ \qquad\qquad\qquad\le c_1n^2|u|_1|v|_1](4D617468656D61746963616C20626173697320666F722046454D_eq0097.gif)
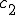 は係数
は係数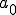 の上限とする。つまり
の上限とする。つまり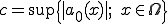 このときCauchy-Schwarzの定理より、
このときCauchy-Schwarzの定理より、
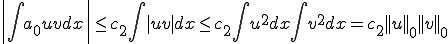
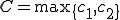 とする。また
とする。また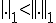 かつ
かつ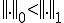 が成り立つから、
が成り立つから、
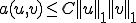 が成り立つ。つまり、関数
が成り立つ。つまり、関数 は有界である。
は有界である。
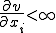 であるので、次のような
であるので、次のような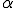 を定めることができる。
を定めることができる。
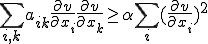
上式を積分して
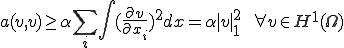
Poincare-Friedrichの不等式より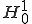 の中では2つのノルム
の中では2つのノルム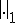 、
、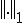 は同一である。つまり
は同一である。つまり
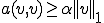 が成り立つ。前に示したとおり有界性も成り立つので関数
が成り立つ。前に示したとおり有界性も成り立つので関数 は
は 内で
内で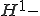 楕円双線形関数である。
楕円双線形関数である。
Lax-Milgramの定理から汎関数の解が一意に存在し、これは特徴化定理からこれは弱い解である。
ある楕円型の境界値問題は、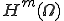 、や
、や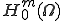 上で関数
上で関数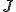 を最小化するような変分問題を解くことで得られた。計算機上で解を求めたい場合は次元の数が限られているので、ある部分空間の中で汎関数の最小値を求め、それを近似解とする。ここで
を最小化するような変分問題を解くことで得られた。計算機上で解を求めたい場合は次元の数が限られているので、ある部分空間の中で汎関数の最小値を求め、それを近似解とする。ここで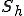 は離散的な関数空間を表し、有限次元の部分空間であるとする。hは離散化パラメーターである。
は離散的な関数空間を表し、有限次元の部分空間であるとする。hは離散化パラメーターである。
次のような変分問題を考える
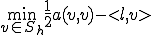
特徴化定理から
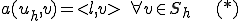
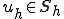 が上式の解であれば、
が上式の解であれば、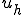 はこの変分問題の解であるということがいえる。ここで関数
はこの変分問題の解であるということがいえる。ここで関数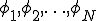 が
が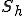 の基底である、つまり
の基底である、つまり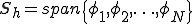 であるとすると、(*)は次に等しい
であるとすると、(*)は次に等しい
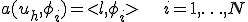
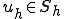 であったので
であったので
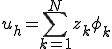
と書くことができる。これを上式に代入して
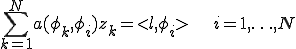
ここで行列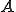 を
を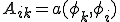 、ベクトル
、ベクトル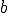 を
を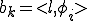 のようにおくと、
のようにおくと、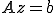 の連立一次方程式の形に書くことができる。
の連立一次方程式の形に書くことができる。
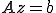 を解くことで
を解くことで を求め、
を求め、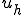 を求める方法をRitz-Galerkin法と呼ぶ。
を求める方法をRitz-Galerkin法と呼ぶ。
Ritz-Galerkin法の解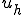 の性質を調べてみよう。ここで正解は
の性質を調べてみよう。ここで正解は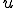 であるとする。
であるとする。
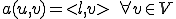
Ritz-Galerkin法より
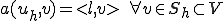
上式を差し引いて
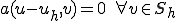
が成り立つ。ここで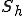 の線形性により、任意の
の線形性により、任意の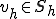 に対して
に対して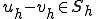 であるから、
であるから、
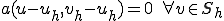
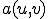 の正定値性、正規性、線形性、対称性よりこの双線形形式は内積としての性質を持ち、
の正定値性、正規性、線形性、対称性よりこの双線形形式は内積としての性質を持ち、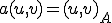 などと書かれる。またこのノルムから作られるノルム
などと書かれる。またこのノルムから作られるノルム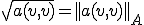 と書き、これをエネルギーノルムと呼ぶ。Ritz-Galerkin法の解
と書き、これをエネルギーノルムと呼ぶ。Ritz-Galerkin法の解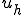 は
は
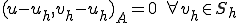
を満たす。つまり、正解とRitz-Galerkin法との差はあらゆる離散空間上のベクトルと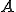 内積で直行している。Ritz-Galerkin法は離散空間上への正解のエネルギーノルムによる正射影であるといえる。これはRitz-Projectorと呼ばれる。
内積で直行している。Ritz-Galerkin法は離散空間上への正解のエネルギーノルムによる正射影であるといえる。これはRitz-Projectorと呼ばれる。
特徴化定理より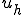 は正解からのAノルムでの距離の2乗を表す次の関数
は正解からのAノルムでの距離の2乗を表す次の関数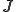
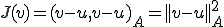
を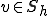 の中で最小化していることがわかる。
の中で最小化していることがわかる。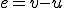 は誤差であるから、Ritz-Galerkin法は誤差のエネルギーノルムを最小化する方法であるといえる。これは誤差最小化原理と呼ばれる。
は誤差であるから、Ritz-Galerkin法は誤差のエネルギーノルムを最小化する方法であるといえる。これは誤差最小化原理と呼ばれる。
| (ユークリッド空間みたいに表した)Ritz-Galerkin法の解の様子 |
|---|
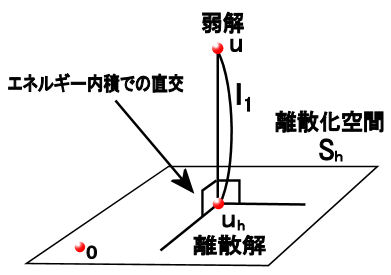 |
離散化解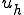 は連続解 は連続解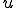 との差は離散空間とエネルギーノルムで直交する。 との差は離散空間とエネルギーノルムで直交する。このとき離散解と連続解との差のエネルギーノルム 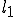 は最小化されている。 は最小化されている。 |
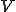 を次のような空間だとする
を次のような空間だとする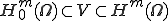 ここで
ここで がV-楕円双線形写像であるとする。また、
がV-楕円双線形写像であるとする。また、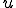 が空間
が空間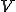 の中の、
の中の、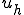 が空間
が空間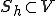 の中における変分問題の解であるとする。このとき
の中における変分問題の解であるとする。このとき
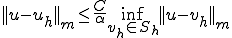
が成り立つ。
Ritz-Galerkin法の解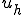 は以下のような性質が成り立った。
は以下のような性質が成り立った。
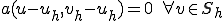
が成り立つ。これを用いて
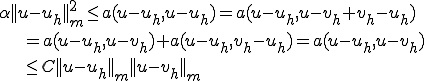
両辺を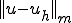 で割って
で割って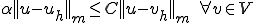 が得られる。
が得られる。
つまり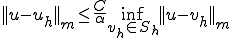 が成り立つ。
が成り立つ。
Céaの補題はRitz-Galerkin法で得られた解がどの程度本当の解に近いのかを評価する上で重要である。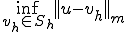 は離散空間上で表現できる中でもっとも正解に近い点の正解との距離を表しており、Ritz-Galerkin法はで得られる解と解析解からの距離は上の定理によって上限が定められている。定義から
は離散空間上で表現できる中でもっとも正解に近い点の正解との距離を表しており、Ritz-Galerkin法はで得られる解と解析解からの距離は上の定理によって上限が定められている。定義から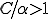 であるが、この値が小さいほど解の近似が良いことを示している。ロッキングなどが起こっているときはこの値が大きく、実際の正解と程遠いような離散解が得られる。また、
であるが、この値が小さいほど解の近似が良いことを示している。ロッキングなどが起こっているときはこの値が大きく、実際の正解と程遠いような離散解が得られる。また、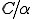 がある程度小さい場合は、Ritz-Galerkin法の解が離散空間上で表現できるもっとも正解に近い解とある程度近いといえるので、解を表現できるように離散空間を設定することでRitz-Galerkin法の解を正解に近づけることができる。
がある程度小さい場合は、Ritz-Galerkin法の解が離散空間上で表現できるもっとも正解に近い解とある程度近いといえるので、解を表現できるように離散空間を設定することでRitz-Galerkin法の解を正解に近づけることができる。
双線形形式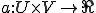 とする。ここで次を満たすように線形写像
とする。ここで次を満たすように線形写像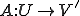 を定める
を定める
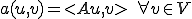
このように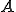 を定義した場合は
を定義した場合は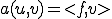 の解は単純に
の解は単純に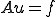 を解けばよい。
を解けばよい。
双線形形式 が次の条件を満たすとき、線形写像
が次の条件を満たすとき、線形写像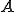 は同型写像である。(
は同型写像である。(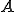 が同型写像であるとは、
が同型写像であるとは、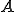 が全単写で有界かつ、
が全単写で有界かつ、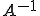 も有界であるということ)
も有界であるということ)
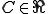 が存在し、
が存在し、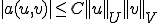
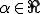 が存在し、
が存在し、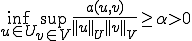
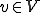 に対して、ある
に対して、ある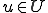 が存在し、
が存在し、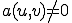 となる。
となる。
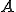 の有界性は
の有界性は の有界性から示される。
の有界性から示される。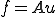 とすると、
とすると、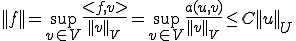
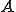 が有界であることがわかる。
が有界であることがわかる。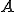 が単写であることはinf-sup条件から明らかである。なぜなら、
が単写であることはinf-sup条件から明らかである。なぜなら、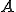 が単写でない
が単写でない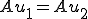 とすると
とすると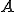 の定義から
の定義から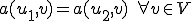 が成り立つ。このことから
が成り立つ。このことから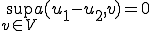 となる。inf-sup条件より全ての
となる。inf-sup条件より全ての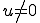 に対して
に対して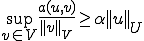
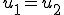 が言える。よって
が言える。よって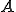 は単写であることがわかる。
は単写であることがわかる。
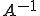 の有界性について示す。
の有界性について示す。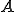 が単写であることがわかったので
が単写であることがわかったので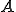 の値域
の値域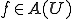 で逆写像が一意にきまる。これを次のように書く
で逆写像が一意にきまる。これを次のように書く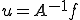 このとき、inf-sup条件から、
このとき、inf-sup条件から、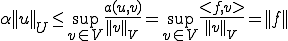
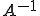 が有界写像であることがわかる。
が有界写像であることがわかる。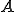 が全写であることを示す。これには3番目の条件を用いる。
が全写であることを示す。これには3番目の条件を用いる。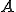 の値域
の値域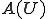 を定めよう。次のような
を定めよう。次のような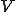 の部分空間
の部分空間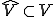 を定める。
を定める。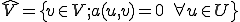 (3番目の条件は
(3番目の条件は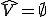 であるといっている。)
であるといっている。)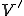 の部分空間
の部分空間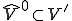 を定める。
を定める。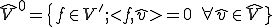
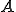 の値域
の値域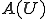 は
は に含まれる、つまり
に含まれる、つまり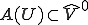 となる。なぜなら、全ての
となる。なぜなら、全ての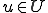 に対して、
に対して、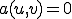 となる
となる について、
について、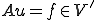 とすると
とすると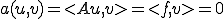 より
より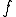 との内積が0となるので
との内積が0となるので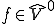 であるからである。
であるからである。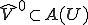 を背理法で示す。仮に
を背理法で示す。仮に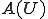 に含まれないような
に含まれないような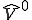 の要素
の要素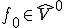 が存在するとする。
が存在するとする。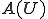 は凸閉空間であるので(閉空間であることは
は凸閉空間であるので(閉空間であることは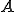 の有界性から明らか)、分離定理より、ある
の有界性から明らか)、分離定理より、ある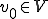 と実数
と実数 が存在し、
が存在し、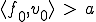 かつ
かつ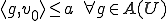
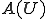 は線形射影だから、明らかに
は線形射影だから、明らかに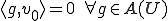 が成り立たなければならない。このとき
が成り立たなければならない。このとき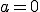 より
より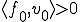 。定義より
。定義より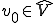 だから
だから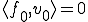 である。これは明らかに
である。これは明らかに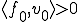 に矛盾する。よって
に矛盾する。よって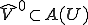 となり、
となり、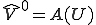 が成り立つ。
が成り立つ。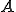 は
は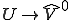 の同型写像である。
の同型写像である。 のとき、定義から明らかに
のとき、定義から明らかに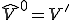 よって、
よって、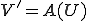 が成り立つ。よって
が成り立つ。よって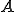 は
は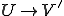 への同型写像である。
への同型写像である。
Lax-Milgramの定理は上の特殊な場合で,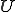 、
、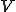 が同じ空間の場合の解の一意存在性と安定性を示している。
が同じ空間の場合の解の一意存在性と安定性を示している。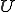 、
、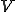 が同じ空間の場合で関数
が同じ空間の場合で関数 が有界性と強圧性を持っている場合、上の定理のi,ii,iiiが成り立つことを確認しよう。
が有界性と強圧性を持っている場合、上の定理のi,ii,iiiが成り立つことを確認しよう。
iの有界性については明らかである。また、
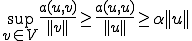
よって強圧性を持っていればiiのinf-sup条件は成り立っている。
また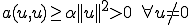 であるからiiiの条件が成り立っている。以上でLax-Millgramの定理が成り立てば、上の定理が成り立つことがわかる。
であるからiiiの条件が成り立っている。以上でLax-Millgramの定理が成り立てば、上の定理が成り立つことがわかる。
上の3番目の条件がない場合について詳しく調べる。有界双線形形式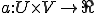 について以下の命題は等しい
について以下の命題は等しい
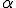 が存在して次を満たす
が存在して次を満たす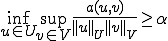
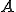 は
は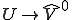 の同型写像で次を満たす
の同型写像で次を満たす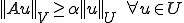
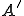 は
は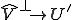 の同型写像で次を満たす
の同型写像で次を満たす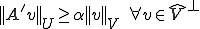
空間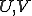 、共役空間 、共役空間 の様子 の様子 |
|---|
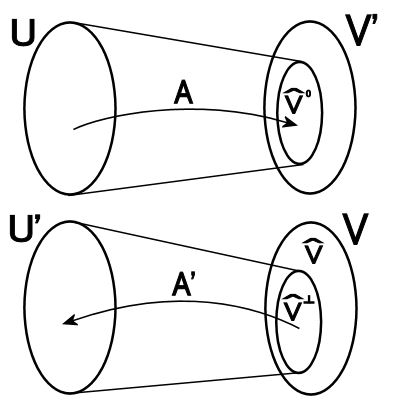 |
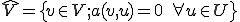 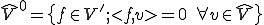 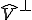 は は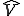 の直交補空間 の直交補空間 |
上から、iとiiは等しい。そこでiiiとiiが等しいことを示す。
iiが成り立ってるとするときにiiiが成り立つことを示す。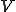 と
と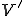 は共役空間なので、Rieszの表現定理からある
は共役空間なので、Rieszの表現定理からある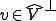 に対して
に対して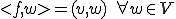 となるような
となるような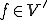 を選ぶことができる。
を選ぶことができる。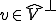 なので
なので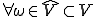 に対して
に対して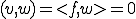 である。
である。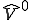 の定義から
の定義から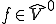 である。さて、iiが成り立っているとすると、写像
である。さて、iiが成り立っているとすると、写像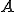 は
は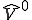 から
から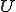 への全単写であったから、ある
への全単写であったから、ある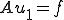 となるような
となるような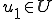 が一意に存在する。
が一意に存在する。
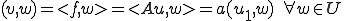
ここでiiが成り立っているので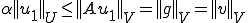
ここで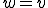 とおくと
とおくと
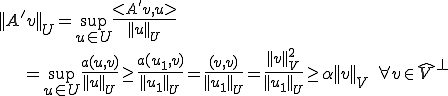
が成り立つ。これを用いるとオペレータ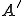 が同型写像であるということが上の定理を使って示すことができる。
が同型写像であるということが上の定理を使って示すことができる。
次にiiiが成り立っているとするときにiが成り立つことを示す。
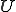 と
と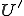 は共役空間なのでそのノルムは次のように書くことができる。
は共役空間なのでそのノルムは次のように書くことができる。
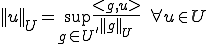
iiiが成り立つことから、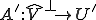 が同型写像なので任意の
が同型写像なので任意の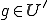 に対して
に対して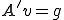 となるような
となるような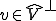 が一意に決まる。よって
が一意に決まる。よって
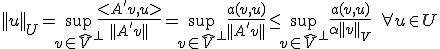
よって
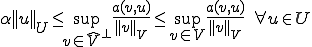
これはiの条件である。よってiiiが成り立つときはiが成り立つ。
以上からi,ii,iiiは互いに等しい命題であることがわかる。
 、
、 をそれぞれHirbert空間とする。
をそれぞれHirbert空間とする。 をそれぞれ次のような有界双線形関数であるとする。
をそれぞれ次のような有界双線形関数であるとする。
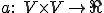
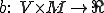
次のような関数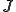 を
を
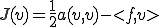
次の制約条件の下で解く
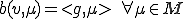
このような制約条件つきの変分問題の代表的な解法としてLagrange未定乗数法が挙げられる。Lagrange未定乗数法を使うとこの問題は次のような関数の極値問題に対応づけることができる。
![\cal{L}(v,\lambda)=J(v)+[b(v,\lambda)-<g,\lambda>] \cal{L}(v,\lambda)=J(v)+[b(v,\lambda)-<g,\lambda>]](4D617468656D61746963616C20626173697320666F722046454D_eq0327.gif)
明らかに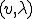 が解である場合に次の関係を満たす(実際は最初の不等号は等号である)
が解である場合に次の関係を満たす(実際は最初の不等号は等号である)
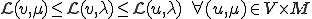
これがこのタイプの問題が鞍点型と呼ばれる所以である。
さて上の関数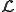 が
が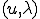 で極値をとる場合、
で極値をとる場合、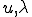 における変分が0であるから
における変分が0であるから
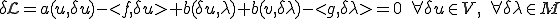
簡単のため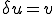 、
、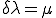 と書くと、
と書くと、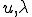 が
が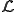 の極値であるということは以下を満たすことに等しい。
の極値であるということは以下を満たすことに等しい。
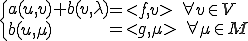
さて上の方程式の解が一意に存在して安定であることを調べてみる。
次のような写像考えると
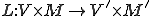
この写像が同型写像(全単写、有界、逆写像が有界)になるためには以下のiとiiが必要十分条件である。
 が
が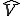 において楕円である。つまり、
において楕円である。つまり、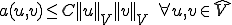
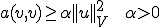
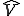 とは制約条件を満たす
とは制約条件を満たす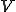 の部分空間である。
の部分空間である。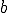 がinf-sup条件を満たす
がinf-sup条件を満たす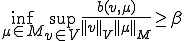
オペレータ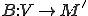 を次のように定義する
を次のように定義する
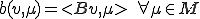
同様にオペレータ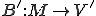 を次のように定義する。
を次のように定義する。
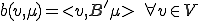
inf-sup条件より次がいえる。
オペレータ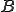 は
は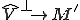 の同型写像であり、
の同型写像であり、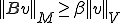 が成り立つ
が成り立つ
オペレータ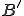 は
は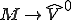 の同型写像であり、
の同型写像であり、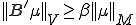 が成り立つ。
が成り立つ。
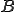 が同型写像であったから、
が同型写像であったから、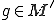 に対してある
に対してある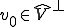 が唯一解として存在して
が唯一解として存在して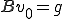 となる。そして
となる。そして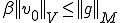 が成り立つ。
が成り立つ。
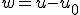 とおくと問題は次の方程式を解くのと等しくなる
とおくと問題は次の方程式を解くのと等しくなる
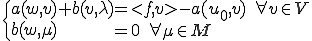
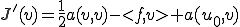 とおくと、上の問題の解
とおくと、上の問題の解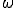 は
は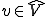 の中で
の中で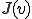 を最小化する解に等しい。aは
を最小化する解に等しい。aは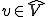 で楕円性を持っていたからLax-Milgramの定理より
で楕円性を持っていたからLax-Milgramの定理より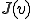 を最小にするような
を最小にするような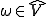 が存在し、そのとき特徴化定理より
が存在し、そのとき特徴化定理より
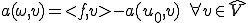 を満たす。
を満たす。
解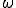 についてCauchy-Schwalzの定理より次が成り立つ。
についてCauchy-Schwalzの定理より次が成り立つ。
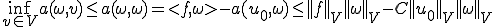
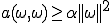
上の2つの式を合わせると次のことがいえる。
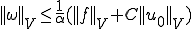
さらに
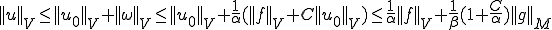
さて、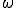 を評価することができたので、もう一つの解
を評価することができたので、もう一つの解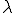 を評価しよう。
を評価しよう。
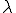 は次の方程式を満たす。
は次の方程式を満たす。
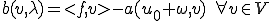
上式より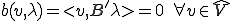 だから、
だから、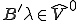 となる。
となる。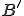 は
は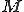 から
から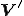 への全単写だったから唯一
への全単写だったから唯一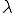 が存在する。
が存在する。
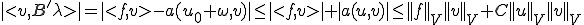
また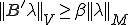 が成り立つことと、
が成り立つことと、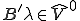 であることを利用して
であることを利用して
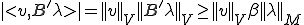 だから、
だから、
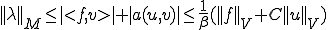
まず、任意の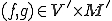 について、解
について、解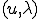 は次のように評価される。
は次のように評価される。
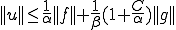
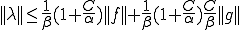
つまり は全写であり、
は全写であり、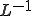 は有界
は有界
次に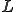 の単写性を示す。
の単写性を示す。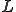 は線形オペレータだから
は線形オペレータだから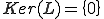 となれば単写である。そこで
となれば単写である。そこで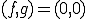 のときに解が
のときに解が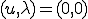 となるかを調べる。この時解くべき方程式は次のとおり
となるかを調べる。この時解くべき方程式は次のとおり
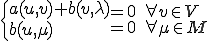
ここで に
に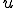 を、
を、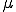 に
に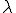 を代入すると
を代入すると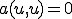 となり、
となり、 の楕円性から
の楕円性から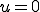 となる。これから
となる。これから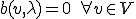 がいえる。inf-sup条件から、
がいえる。inf-sup条件から、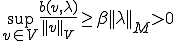 であるから、
であるから、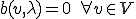 となるのは
となるのは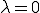 のときのみ。よって
のときのみ。よって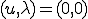 がいえる。よって
がいえる。よって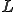 が単写であることがわかる。
が単写であることがわかる。
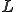 の有界性は
の有界性は 、
、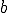 の有界性から明らか。
の有界性から明らか。
以上から、上の条件が成り立つとき、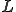 が同型写像であることがわかる。
が同型写像であることがわかる。
| 有限要素法の数理 | 菊池文雄 著 |
| 有限要素法概説 | 菊池文雄 著 |
| 非線形有限要素法の基礎と応用 | 野口裕久 久田俊明 著 |
| Finite Element Procedures | Klaus-Jurgen Bathe 著 |
| Finite Elements: Theory, Fast Solvers, and Applications in Solid Mechanics | Dietrich Braess 著 |