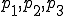 からなる三角形の面積
からなる三角形の面積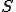 は次のように表すことができる。
は次のように表すことができる。|TOP Page|
点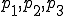 からなる三角形の面積
からなる三角形の面積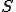 は次のように表すことができる。
は次のように表すことができる。
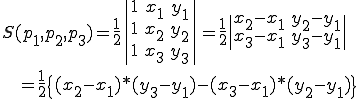
また、ヘロンの公式によれば、3角形の3辺の長さを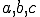 、
、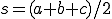 としたとき
としたとき
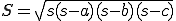
が成り立つ。
double TriArea(const CVector2D& v1, const CVector2D& v2, const CVector2D& v3){
return 0.5*( (v2.x-v1.x)*(v3.y-v1.y) - (v3.x-v1.x)*(v2.y-v1.y) );
}
3角形の周の長さの半分を 、面積を
、面積を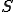 とすると、内接円の半径
とすると、内接円の半径 は
は
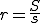
となる。
三角形の面積を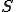 、3辺の長さを
、3辺の長さを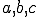 とすると、外接円の半径
とすると、外接円の半径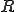 は
は
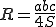
が成り立つ。
3角形のアスペクト比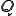 は、外接円の半径
は、外接円の半径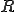 、内接円の半径
、内接円の半径 とすると次のように定義される。
とすると次のように定義される。
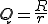
3角形の質を評価するためにアスペクト比がよく用いられる。三角形の三辺の長さを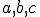 、
、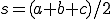 とおくと、ヘロンの公式を使って、アスペクト比
とおくと、ヘロンの公式を使って、アスペクト比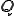 は次のようになる。
は次のようになる。
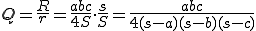
点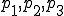 で与えられる、3角形の外接円の中心
で与えられる、3角形の外接円の中心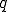 は
は
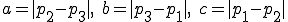 とすると、
とすると、
![q=\[a^2(b^2+c^2-a^2)p_1+b^2(c^2+a^2-b^2)p_2+c^2(a^2+b^2-c^2)p_3\]/(16S^2) q=\[a^2(b^2+c^2-a^2)p_1+b^2(c^2+a^2-b^2)p_2+c^2(a^2+b^2-c^2)p_3\]/(16S^2)](A5E1A5C3A5B7A5E5C0B8C0AEA4CEA5D7A5EDA5B0A5E9A5DFA5F3A5B054495053_eq0026.gif)
によって与えられる。但し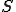 は3角形の面積
は3角形の面積
外接円の中心の求め方は、こちらを参考にした。
bool CenterCircumcircle(
const CVector2D& p0,
const CVector2D& p1,
const CVector2D& p2,
CVector2D& center){
const double area = TriArea(p0,p1,p2);
if( fabs(area) < 1.0e-10 ){ return false; }
const double tmp_val = 1.0/(area*area*16.0);
const double dtmp0 = SquareLength(p1,p2);
const double dtmp1 = SquareLength(p0,p2);
const double dtmp2 = SquareLength(p0,p1);
const double etmp0 = tmp_val*dtmp0*(dtmp1+dtmp2-dtmp0);
const double etmp1 = tmp_val*dtmp1*(dtmp0+dtmp2-dtmp1);
const double etmp2 = tmp_val*dtmp2*(dtmp0+dtmp1-dtmp2);
center.x = etmp0*p0.x + etmp1*p1.x + etmp2*p2.x;
center.y = etmp0*p0.y + etmp1*p1.y + etmp2*p2.y;
return true
}
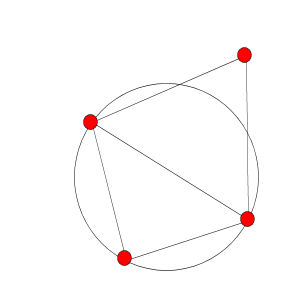
2次元3角形分割の場合はドロネー分割がある種の最適な分割である。ドロネー三角分割とは、3角形の外接円に他の三角形の頂点が入っていないことである。これをチェックするプログラムを考えよう。
| Delaunay条件を満たす三角形 | Delaunay条件を満たさない三角形 |
|---|---|
 |
 |
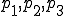 を頂点とする三角形について、
を頂点とする三角形について、
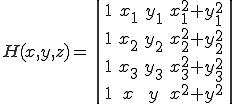
は
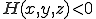 三角形の外接円の内側の式
三角形の外接円の内側の式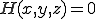 三角形の外接円の式
三角形の外接円の式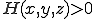 三角形の外接円の外側式
三角形の外接円の外側式
となる。さて、点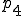 がこの外接円に入っているかどうか調べよう。これには
がこの外接円に入っているかどうか調べよう。これには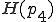 の符号を調べればよい。
の符号を調べればよい。
余因子展開を用いてこれは次のように書ける。
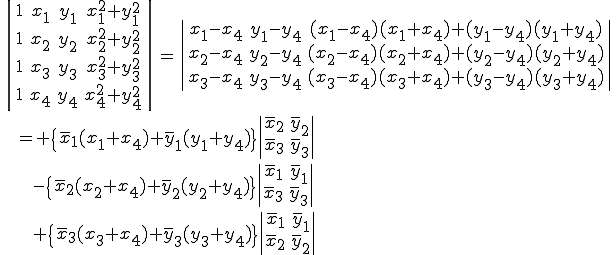
但し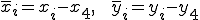 である。
である。
double DetDelaunay(
const CVector2D& p0,
const CVector2D& p1,
const CVector2D& p2,
const CVector2D& p3){
a[6] = {
p0.x-p3.x // 0
p1.x-p3.x // 1
p2.x-p3.x // 2
p0.y-p3.y // 3
p1.y-p3.y // 4
p2.y-p3.y // 5
};
return +(a[0]*(p0.x+p3.x)+a[3]*(p0.y+p3.y))*(a[1]*a[5]-a[2]*a[4])
-(a[1]*(p1.x+p3.x)+a[4]*(p1.y+p3.y))*(a[0]*a[5]-a[2]*a[3])
+(a[2]*(p2.x+p3.x)+a[5]*(p2.y+p3.y))*(a[0]*a[4]-a[1]*a[3]);
}
外積を利用して、面積を求める。
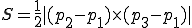
double TriArea(const CVector3D& v1, const CVector3D& v2, const CVector3D& v3)
{
double x, y, z;
x = ( v2.y - v1.y )*( v3.z - v1.z ) - ( v3.y - v1.y )*( v2.z - v1.z );
y = ( v2.z - v1.z )*( v3.x - v1.x ) - ( v3.z - v1.z )*( v2.x - v1.x );
z = ( v2.x - v1.x )*( v3.y - v1.y ) - ( v3.x - v1.x )*( v2.y - v1.y );
return 0.5*sqrt( x*x + y*y + z*z );
}
点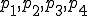 からなる四面体の体積
からなる四面体の体積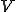 は次のとおり。
は次のとおり。
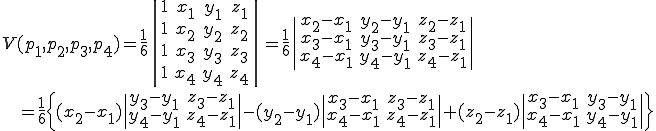
double TetVolume(
const CVector3D& v1,
const CVector3D& v2,
const CVector3D& v3,
const CVector3D& v4 )
{
return
( ( v2.x - v1.x )*( ( v3.y - v1.y )*( v4.z - v1.z ) - ( v4.y - v1.y )*( v3.z - v1.z ) )
- ( v2.y - v1.y )*( ( v3.x - v1.x )*( v4.z - v1.z ) - ( v4.x - v1.x )*( v3.z - v1.z ) )
+ ( v2.z - v1.z )*( ( v3.x - v1.x )*( v4.y - v1.y ) - ( v4.x - v1.x )*( v3.y - v1.y ) )
) * 0.16666666666666666666666666666667;
}
四面体の体積を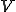 、表面積を
、表面積を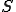 とする。
とする。
内接球の半径を は
は
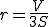
となる。
double InscribedRadius(
const CVector3D& ipo0,
const CVector3D& ipo1,
const CVector3D& ipo2,
const CVector3D& ipo3)
double surface = TriArea( ipo1, ipo3, ipo2 )
+ TriArea( ipo0, ipo2, ipo3 )
+ TriArea( ipo0, ipo3, ipo1 )
+ TriArea( ipo0, ipo1, ipo2 );
return TetVolume(ipo0, ipo1, ipo2, ipo3) * 3.0 / surface;
}
外心の座標を求めるために、外接円の中心の座標を求めて、頂点からの距離を計算する。
外心の座標の求め方についてはこちらを参考にした。
inline double Circumradius(
const CVector3D& ipo0,
const CVector3D& ipo1,
const CVector3D& ipo2,
const CVector3D& ipo3)
{
double base[3][3] = {
{ ipo1.x-ipo0.x, ipo1.y-ipo0.y, ipo1.z-ipo0.z },
{ ipo2.x-ipo0.x, ipo2.y-ipo0.y, ipo2.z-ipo0.z },
{ ipo3.x-ipo0.x, ipo3.y-ipo0.y, ipo3.z-ipo0.z }
};
double s[6] = {
base[0][0]*base[0][0]+base[0][1]*base[0][1]+base[0][2]*base[0][2],
base[1][0]*base[1][0]+base[1][1]*base[1][1]+base[1][2]*base[1][2],
base[2][0]*base[2][0]+base[2][1]*base[2][1]+base[2][2]*base[2][2],
base[1][0]*base[2][0]+base[1][1]*base[2][1]+base[1][2]*base[2][2],
base[2][0]*base[0][0]+base[2][1]*base[0][1]+base[2][2]*base[0][2],
base[0][0]*base[1][0]+base[0][1]*base[1][1]+base[0][2]*base[1][2],
};
const double vol = TetVolume(ipo0,ipo1,ipo2,ipo3)*6.0;
if( vol < 1.0e-20 ){
std::cout << "Error!-->Too Small " << std::endl;
assert(0);
}
const double inv_det = 1.0 / (vol*vol);
double t[6] = {
(s[1]*s[2]-s[3]*s[3])*0.5*inv_det,
(s[2]*s[0]-s[4]*s[4])*0.5*inv_det,
(s[0]*s[1]-s[5]*s[5])*0.5*inv_det,
(s[4]*s[5]-s[0]*s[3])*0.5*inv_det,
(s[5]*s[3]-s[1]*s[4])*0.5*inv_det,
(s[3]*s[4]-s[2]*s[5])*0.5*inv_det,
};
double u[3] = {
t[0]*s[0]+t[5]*s[1]+t[4]*s[2],
t[5]*s[0]+t[1]*s[1]+t[3]*s[2],
t[4]*s[0]+t[3]*s[1]+t[2]*s[2],
};
return sqrt(0.5*(u[0]*s[0]+u[1]*s[1]+u[2]*s[2]));
}
次の論文のように、直接外接球の半径を求める方法もあるらしい。ただ、2次元の場合と違ってあまり単純にはならない。
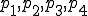 を頂点とする四面体について、
を頂点とする四面体について、

は
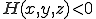 のとき四面体の外接球の内側の方程式
のとき四面体の外接球の内側の方程式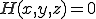 のとき四面体の外接球の方程式
のとき四面体の外接球の方程式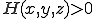 のとき四面体の外接球の外側の方程式
のとき四面体の外接球の外側の方程式を与える。
点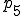 がこの四面体の中に入っているかどうか調べるためには次の符号を調べればよい。
がこの四面体の中に入っているかどうか調べるためには次の符号を調べればよい。
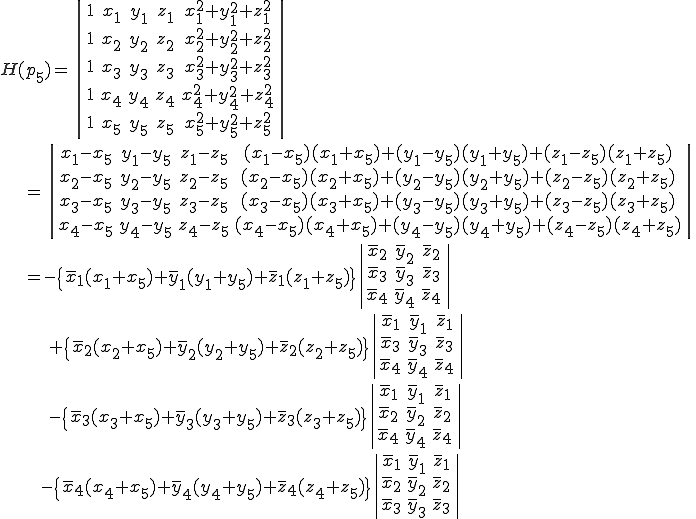
double DetDelaunay3D(
const CVector3D& v1,
const CVector3D& v2,
const CVector3D& v3,
const CVector3D& v4,
const CVector3D& v5)
{
const double a[12] = {
v1.x-v5.x, // 0
v2.x-v5.x, // 1
v3.x-v5.x, // 2
v4.x-v5.x, // 3
v1.y-v5.y, // 4
v2.y-v5.y, // 5
v3.y-v5.y, // 6
v4.y-v5.y, // 7
v1.z-v5.z, // 8
v2.z-v5.z, // 9
v3.z-v5.z, // 10
v4.z-v5.z, // 11
};
const double b[6] = {
a[ 6]*a[11]-a[ 7]*a[10], // 0
a[ 5]*a[11]-a[ 7]*a[ 9], // 1
a[ 5]*a[10]-a[ 6]*a[ 9], // 2
a[ 7]*a[ 8]-a[ 4]*a[11], // 3
a[ 6]*a[ 8]-a[ 4]*a[10], // 4
a[ 4]*a[ 9]-a[ 5]*a[ 8], // 5
};
return -( a[0]*(v1.x+v5.x)+a[4]*(v1.y+v5.y)+a[ 8]*(v1.z+v5.z) )*( a[ 1]*b[0]-a[ 2]*b[1]+a[ 3]*b[2] )
+( a[1]*(v2.x+v5.x)+a[5]*(v2.y+v5.y)+a[ 9]*(v2.z+v5.z) )*( a[ 0]*b[0]+a[ 2]*b[3]-a[ 3]*b[4] )
-( a[2]*(v3.x+v5.x)+a[6]*(v3.y+v5.y)+a[10]*(v3.z+v5.z) )*( a[ 0]*b[1]+a[ 1]*b[3]+a[ 3]*b[5] )
+( a[3]*(v4.x+v5.x)+a[7]*(v4.y+v5.y)+a[11]*(v4.z+v5.z) )*( a[ 0]*b[2]+a[ 1]*b[4]+a[ 2]*b[5] );
}