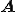 を非対称行列とすると、双ランチョス法は非対称行列のために双直交な
を非対称行列とすると、双ランチョス法は非対称行列のために双直交な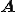 と
と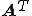 のクリロフ部分空間の基底を作成する方法である。
のクリロフ部分空間の基底を作成する方法である。|TOP Page|
双ランチョス法(Two-Sided Lanczos Method)はランチョス双直交化(Lanczos Biorthogonalization)とも呼ばれる
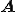 を非対称行列とすると、双ランチョス法は非対称行列のために双直交な
を非対称行列とすると、双ランチョス法は非対称行列のために双直交な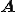 と
と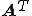 のクリロフ部分空間の基底を作成する方法である。
のクリロフ部分空間の基底を作成する方法である。
ここで、クリロフ部分空間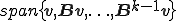 を
を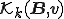 と表すとする。
と表すとする。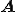 のクリロフ部分空間の基底を
のクリロフ部分空間の基底を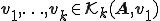 、
、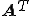 のクリロフ部分空間の基底を
のクリロフ部分空間の基底を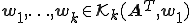 とすると、双直交な
とすると、双直交な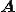 と
と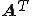 のクリロフ部分空間の基底とは、
のクリロフ部分空間の基底とは、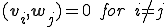 を満たすような2つの基底である。
を満たすような2つの基底である。
対称行列はLanczos法を用いることで、3項間漸化式を作ることによって正規直交基底を作ることができた。同様に双ランチョス法では、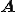 と
と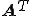 に対する2つの基底に対してそれぞれ3項間漸化式を作ることで逐次的に新しい基底を求める。
に対する2つの基底に対してそれぞれ3項間漸化式を作ることで逐次的に新しい基底を求める。
双ランチョス法はBiCG法などの方法に応用される。
双ランチョス法では次のようにして双直交なクリロフ部分空間の基底を求める。
1. Chose two vectors 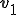 ,
,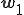 such that
such that 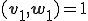
2. Set 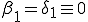 ,
, 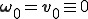
3. For 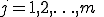 Do:
Do:
4. 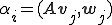
5. 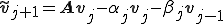
6. 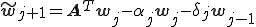
7. 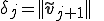 If
If 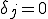 Stop
Stop
8. 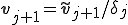
9. 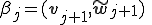 And
And 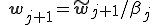
10. End Do
手順7,8,9では、三項間漸化式によって得られた新しい基底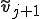 、
、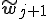 に対して、
に対して、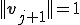 、
、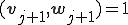 が成り立つようにスケーリングしてある。このスケーリングの仕方は
が成り立つようにスケーリングしてある。このスケーリングの仕方は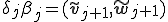 の関係さえ満たせばどのように選んでも双直交な基底が得られるが、このように
の関係さえ満たせばどのように選んでも双直交な基底が得られるが、このように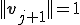 、
、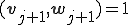 が成り立つようにスケーリングすると、後々の議論に大変便利である。これ以降ではこのスケーリングを用いるものとする。
が成り立つようにスケーリングすると、後々の議論に大変便利である。これ以降ではこのスケーリングを用いるものとする。
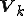 は行ベクトルが基底
は行ベクトルが基底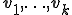 である行列であるとし、
である行列であるとし、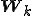 は行ベクトルが基底
は行ベクトルが基底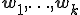 である行列であるとする。
である行列であるとする。
基底の双直交性は次のようにあらわされる。
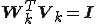
ここで、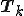 は大きさが[k,k]の次のような3重対角行列であるとすると、
は大きさが[k,k]の次のような3重対角行列であるとすると、
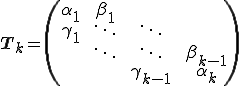
但し、ここでの係数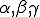 はアルゴリズムの中の3項間漸化式で導入したものと同一である。
はアルゴリズムの中の3項間漸化式で導入したものと同一である。
三項漸化式の関係から明らかに以下が成り立つ。
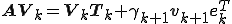
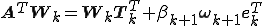
また上式から
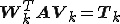 |
が成り立つ。この関係式は固有値を求める時や連立一次方程式を解く時などに使う
ここで、この双ランチョス法の手続きによって得られる、2つの基底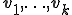 と
と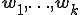 が双直交であることを証明する。
が双直交であることを証明する。
この2つの基底が双直交であるというのは、
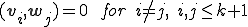
ということである。
以下帰納法を使って証明する。
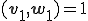 より、明らかに成り立つ。
より、明らかに成り立つ。
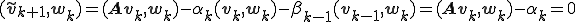
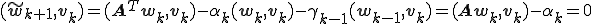
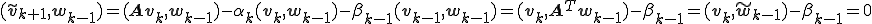
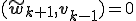
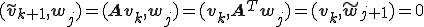
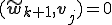
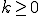 で成り立つことがわかる。
で成り立つことがわかる。ランチョス双直交化法で作られた2つのクリロフ部分空間の基底を使って連立一次方程式を解くことができる。連立一次方程式を解くやり方も双ランチョス法(Two-Sided Lanczos Method)と呼ばれているようである。双ランチョス法で連立一次方程式を解くやり方はBiCG法と深い関係がある。
k反復目の解を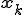 、残差を
、残差を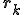 とすると、双ランチョス法で連立一次方程式を解くやり方は、残差がクリロフ部分空間
とすると、双ランチョス法で連立一次方程式を解くやり方は、残差がクリロフ部分空間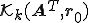 と直交するような解をクリロフ部分空間
と直交するような解をクリロフ部分空間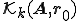 の中から探すという方法である。つまり、
の中から探すという方法である。つまり、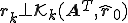 となるように、
となるように、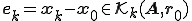 を見つけるというものである。
を見つけるというものである。
ランチョス双直交化で得られた2つの基底を並べた行列を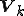 、
、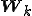 とすると、これらは次のように書き換えることができる。
とすると、これらは次のように書き換えることができる。
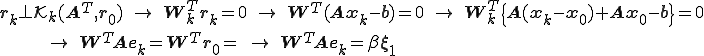
ここで、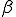 は
は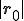 である。また、
である。また、
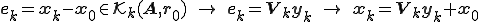
とかける、ここで、ベクトル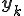 は
は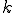 次元のベクトルである。
次元のベクトルである。
これらを合わせると次のようになる。
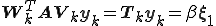
これを解くことで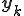 を求め、
を求め、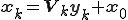 によって解を求めることができる。
によって解を求めることができる。
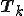 は3重対角行列なので、
は3重対角行列なので、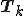 のLU分解は容易に計算できる。また、この性質を生かしてクリロフ部分空間の全ての基底
のLU分解は容易に計算できる。また、この性質を生かしてクリロフ部分空間の全ての基底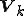 を保存しておかなくても、前回の反復における解の更新から、次の反復における解の更新を求めることができる。
を保存しておかなくても、前回の反復における解の更新から、次の反復における解の更新を求めることができる。
BiCG法はこの方法の一種であるが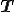 について解く必要がなく、簡単なので一般的によく使われている。
について解く必要がなく、簡単なので一般的によく使われている。