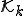 の正規直交基底
の正規直交基底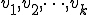 を求める。
を求める。|TOP Page|
Arnoldi法はKrylov部分空間の正規直交規定を求める方法である。
QR法により非対称行列の固有値を求める時やGMRes法による連立一次方程式の求解に使われる。
Arnoldi法はGram-Shumitの直交化に従ってKrylov部分空間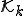 の正規直交基底
の正規直交基底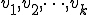 を求める。
を求める。
1. Chose a vector 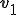 of norm 1
of norm 1
2. For 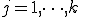 Do:
Do:
3. 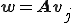
4. For 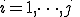 Do:
Do:
5. 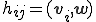
6. 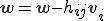
7. End Do
8. 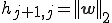
9. If 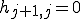 then Stop
then Stop
10. 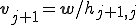
11. End Do
3行目でj番目の基底を求めた後、4,5,6,7行目でGram-Shumitの直交化を行い、j番目の基底を1〜j-1番目の正規直交基底と直交させる。8,9,10行目で直交化させた基底を正規化している。
Arnodi法のアルゴリズムから以下の式が成立つ。
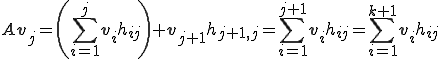
ここで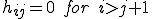 を用いた
を用いた
ここで、行列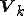 を行ベクトルが
を行ベクトルが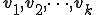 である
である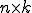 の行列であるとする。また、行列
の行列であるとする。また、行列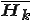 はij成分がArnodi法のアルゴリズムの際の
はij成分がArnodi法のアルゴリズムの際の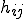 である、
である、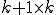 の行列であるとする。すると、以下の式が成立つ。
の行列であるとする。すると、以下の式が成立つ。
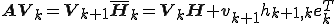
ここで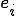 は次のような単位ベクトルである。
は次のような単位ベクトルである。
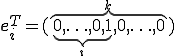
左から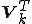 をかけると、
をかけると、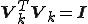 ,
,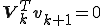 より
より
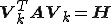
が成立つ。
グラムシュミット(Gram-Shumit)の直交化の代わりに修正グラムシュミット(Modefied Gram-Shumit)の直交化を用いると、数学的には結果は変化しないが、丸め誤差の影響が小さくすることができ、精度の高い直交化ができる。修正グラムシュミットの直交化を用いたArnoldi法のアルゴリズムは以下のとおり
1. Chose a vector 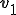 of norm 1
of norm 1
2. For 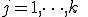 Do:
Do:
3. 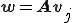
4. For 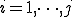 Do:
Do:
5. 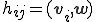
6. 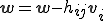
7. End Do
8. 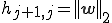
9. If 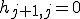 then Stop
then Stop
10. 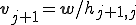
11. End Do
5行目において修正グラムシュミットのアルゴリズムはグラムシュミットのアルゴリズムと違って1からi-1番目の正規直行基底を取り除いたベクトル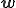 に対して内積を計算している。
に対して内積を計算している。