 ��)�D���b�V���͑S�Ẳ�͗̈�ߐs�����悤�ɍ���܂��D�ł�����C��͗̈���̂P�_�͕K������v�f�����̋��E��ɂ���͂��ł��D�_���܂܂��v�f���₻�̕ӂł̕�Ԃ����߂�Ή�͗̈���̔C�ӂ̓_�̒l�����܂�܂��D�v�f���₻�̋��E�ŘA���ȕ�Ԃ�p���Ă���̂ŁC���̏�͘A���ł��邱�Ƃ��킩��܂��D
��)�D���b�V���͑S�Ẳ�͗̈�ߐs�����悤�ɍ���܂��D�ł�����C��͗̈���̂P�_�͕K������v�f�����̋��E��ɂ���͂��ł��D�_���܂܂��v�f���₻�̕ӂł̕�Ԃ����߂�Ή�͗̈���̔C�ӂ̓_�̒l�����܂�܂��D�v�f���₻�̋��E�ŘA���ȕ�Ԃ�p���Ă���̂ŁC���̏�͘A���ł��邱�Ƃ��킩��܂��D|TOP Page|
�L���v�f�@�Ƃ́C���b�V����p���ċ�ԓI�ɗ��U�����ꂽ���̒�������`�������ꂽ�Δ����������̉�����������@�ł��D
�����I�ȕ��ʂ̏�͖����̎����������܂����C�R���s���[�^�Ŗ��������̏�͖ܘ_�\���ł��Ȃ��̂ŁC�v�Z�@��ł͗L���̒l�ŏ��\�����܂��D���ꂪ"�L��"�v�f�@�ƌĂ�鏊�Ȃł��D�ł͂ǂ̂悤�ɂ��āC���L���̕ϐ����g���ĕ\�����Ă���̂����Ă݂܂��傤�D
�L���v�f�@�ɂ���̃f�[�^�\��(�L���v�f�@��ԏ�)�̓��b�V����p���Ă��܂��D���b�V���͉�͗̈��P���ȑ��p�`�Łi�Q�����̏ꍇ�͎O�p�`��S�p�`�C�R�����̏ꍇ�͂S�ʑ́C�U�ʑ́j�����������̂ł��D�L���v�f�@��Ԃ��ꂽ��͐ߓ_�z��Ɨv�f�z��̂Q���Z�b�g�ɂ��č���܂��D
�ߓ_�Ƃ͋�ԏ�̈�_�ŁC���̓_�ɂ������̒l�������܂��D�ߓ_�z��͐ߓ_�̍��W�Ə�̒l(���x�C�ψʂȂ�)������ł���z��ł��D
�ߓ_�����ł͐ߓ_�ȊO�̏ꂪ�ǂ��Ȃ��Ă���̂��͂킩��܂���D�����ŗv�f���g���܂��D�v�f�̓��b�V���̒��̂P�̑��p�`�ŁC���̗v�f���ǂ̐ߓ_�������Ă��邩�Ƃ������������Ă��܂��i�v�͐ߓ_Index�̏W�܂�ł��j�D�v�f�̒��͕�Ԋ���p���ĕ�Ԃ���Ă��܂��D
�ׂ荇���v�f�ԂŐߓ_�����L���Ă���̂ŁC�ꂪ�s�A���ɂȂ邱�Ƃ͂���܂���( ��)�D���b�V���͑S�Ẳ�͗̈�ߐs�����悤�ɍ���܂��D�ł�����C��͗̈���̂P�_�͕K������v�f�����̋��E��ɂ���͂��ł��D�_���܂܂��v�f���₻�̕ӂł̕�Ԃ����߂�Ή�͗̈���̔C�ӂ̓_�̒l�����܂�܂��D�v�f���₻�̋��E�ŘA���ȕ�Ԃ�p���Ă���̂ŁC���̏�͘A���ł��邱�Ƃ��킩��܂��D
��)�D���b�V���͑S�Ẳ�͗̈�ߐs�����悤�ɍ���܂��D�ł�����C��͗̈���̂P�_�͕K������v�f�����̋��E��ɂ���͂��ł��D�_���܂܂��v�f���₻�̕ӂł̕�Ԃ����߂�Ή�͗̈���̔C�ӂ̓_�̒l�����܂�܂��D�v�f���₻�̋��E�ŘA���ȕ�Ԃ�p���Ă���̂ŁC���̏�͘A���ł��邱�Ƃ��킩��܂��D
���̂悤�ȃ��b�V���̗v�f�z��͎��̂悤�ɂȂ�D
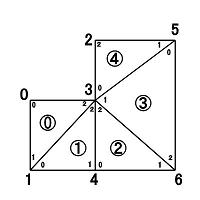 |
�v�f�z��
| �v�f�ԍ� | �ߓ_Index |
|---|---|
| 0 | 0 1 3 |
| 1 | 1 4 3 |
| 2 | 4 6 3 |
| 3 | 5 3 6 |
| 4 | 3 5 2 |
��`���͕Δ����������������ƍL���͈͂ʼn�������悤�ɂ����g���ł��D���`���ł͂Q�A���ɔ����\( ��)�Ƃ������ɂ��Ȃ苭�����炩�����v������܂������C��`���ł͂P�K�̎�������ϕ�(
��)�Ƃ������ɂ��Ȃ苭�����炩�����v������܂������C��`���ł͂P�K�̎�������ϕ�(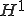 ��)�ł���悭�C���Ȃ�L���͈͂ʼn�����邱�Ƃ��ł��܂��D�L���v�f�@��Ԃ��ꂽ��͗v�f�̐ڑ������Ŕ������s�\�ł��邱�Ƃ������ł��D�Ⴆ�P�����̂P����Ԃ͐܂��(�敪�ꎟ��)�ɂȂ�̂ŁC�����ł̔����͒�`����܂���D������������Ȃ炱�̂悤�Ȋ������������邱�Ƃ��ł��܂��D���`���̉������݂���C����͎�`���̉�(����Ƃ���)�ɂ��Ȃ��Ă��܂��D��`���͋��`���̎��R�Ȋg���ɂȂ��Ă��܂��D
��)�ł���悭�C���Ȃ�L���͈͂ʼn�����邱�Ƃ��ł��܂��D�L���v�f�@��Ԃ��ꂽ��͗v�f�̐ڑ������Ŕ������s�\�ł��邱�Ƃ������ł��D�Ⴆ�P�����̂P����Ԃ͐܂��(�敪�ꎟ��)�ɂȂ�̂ŁC�����ł̔����͒�`����܂���D������������Ȃ炱�̂悤�Ȋ������������邱�Ƃ��ł��܂��D���`���̉������݂���C����͎�`���̉�(����Ƃ���)�ɂ��Ȃ��Ă��܂��D��`���͋��`���̎��R�Ȋg���ɂȂ��Ă��܂��D
��`���ł�����d�v�Ȃ��Ƃ́C���ꂪ�ϕ��`���ł���C�ϕ��̌`�ŏ�����Ă���Ƃ������Ƃł��D�ϕ��͗̈���ł̑����Z�̂悤�ȉ��Z�ł��C��͗̈悪�v�f�ŏ[�U����Ă���̂ŁC�e�v�f���ɐϕ��l�𑫂��Ă����Η̈�S�̂̐ϕ��l�����߂邱�Ƃ��ł��܂��D�e�v�f�͒P���Ȍ`�����Ă���̂ŁC�v�f���ł̐ϕ��͐��l�I,��͓I���@���g���ĊȒP�ɂł��܂��D�ϕ����ł���Ƃ����̂́C��ԏ�����̂ƕ���Ń��b�V���̏d�v�ȋ@�\�ł��D
�|�A�\�����������ɂƂ��āC��`����������Ă݂܂��D
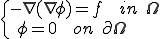
��̋��`����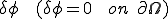 ���|���C�̈�Őϕ��������Green-Gauss�̌������g���ƈȉ��̂悤�Ȏ�`���ɕϊ��ł���D
���|���C�̈�Őϕ��������Green-Gauss�̌������g���ƈȉ��̂悤�Ȏ�`���ɕϊ��ł���D
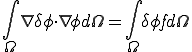
�L���v�f�@�̑����̖���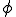 �̑������Ԃɋ����ȋ�Ԃ̌��ł���
�̑������Ԃɋ����ȋ�Ԃ̌��ł���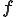 (Riesz�̕\���藝�ɂ��)�Ƒo�ꎟ�`���̍�p�f
(Riesz�̕\���藝�ɂ��)�Ƒo�ꎟ�`���̍�p�f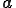 ���g���Ď��̂悤�ɏ����܂��D
���g���Ď��̂悤�ɏ����܂��D
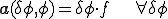
����̓|�e���V����
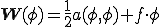
�Ƃ����ꍇ�̃|�e���V�����̋ɒl�����ł��邱�Ƃ��Ӗ����Ă��܂��D
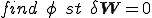
 �̓m�����Ƃ��Ă̐����������Ă��Ă�����G�l���M�[�m�����Ƃ����܂��D����ɁC��p�f
�̓m�����Ƃ��Ă̐����������Ă��Ă�����G�l���M�[�m�����Ƃ����܂��D����ɁC��p�f �̋�������L�E���Ȃǂ̐�������C����͗B�ꑶ�݂��邱�Ƃ��킩��܂��D����ĉ��̓|�e���V�����ŏ��l�ł��邱�Ƃ��킩��܂��D
�̋�������L�E���Ȃǂ̐�������C����͗B�ꑶ�݂��邱�Ƃ��킩��܂��D����ĉ��̓|�e���V�����ŏ��l�ł��邱�Ƃ��킩��܂��D
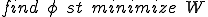
���̃|�e���V�����͕����I�Ȗ��������Ƒ��̏ꍇ�G�l���M�[�Ɠ����ɂȂ�܂��D�Ⴆ�Όő̗͊w��͂ɂ�����|�e���V�����͘c�G�l���M�[��\���܂��D�d���C�ɂ�����|�e���V�������d����̃G�l���M�[��\���܂��D�|�e���V�������ŏ��ł���Ƃ������Ƃ́C�G�l���M�[�ŏ����̌����Ɠ������Ƃł��D
���āC���Ɏ�`�������ꂽ�Δ����������ɗL���v�f�@��ԏ�������ĘA���ꎟ������������Ă݂܂��傤�D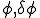 �����̂悤�ɐߓ_�ɂ�����l
�����̂悤�ɐߓ_�ɂ�����l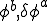 �Ə�̊���
�Ə�̊���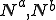 �Ƃ̐ς̘a�ŕ\����Ă���Ƃ��܂��傤�D
�Ƃ̐ς̘a�ŕ\����Ă���Ƃ��܂��傤�D
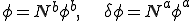
�����O�̎��ɑ������Ɖ����ׂ��A���ꎟ�������������܂��D

����ꂽ�A���ꎟ���������������Ƃʼn��܂��D���ۂ̌W���s��̐���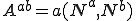 �̌v�Z�́C�v�f���Ƃɍs���C�����𑫂����킹�č��܂��D���̌v�Z�ɂ��ă|�A�\���������̏ꍇ�ɂ��Č��Ă݂܂��傤�D
�̌v�Z�́C�v�f���Ƃɍs���C�����𑫂����킹�č��܂��D���̌v�Z�ɂ��ă|�A�\���������̏ꍇ�ɂ��Č��Ă݂܂��傤�D
��`�������ꂽ�|�A�\���������͎��̂Ƃ���ł����D
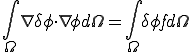
�ϕ��̌v�Z�͗v�f���Ƃɍs�������̑����Z�ł��D
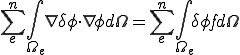
�v�f����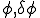 �����̂悤�ɐߓ_�ɂ�����l
�����̂悤�ɐߓ_�ɂ�����l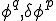 �Ə�̊���
�Ə�̊���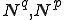 �Ƃ̐ς̘a�ŕ\����Ă���Ƃ��܂��傤�D
�Ƃ̐ς̘a�ŕ\����Ă���Ƃ��܂��傤�D
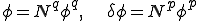
�܂��C�v�f���̔ԍ��Â�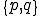 �͐ߓ_�̔ԍ��Â�
�͐ߓ_�̔ԍ��Â�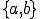 �ɑΉ����Ă���Ƃ��܂��D�����������Ə�̎��͎��̂悤�ɂȂ�܂��D
�ɑΉ����Ă���Ƃ��܂��D�����������Ə�̎��͎��̂悤�ɂȂ�܂��D
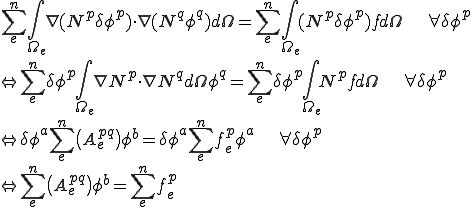
������
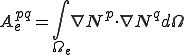
�͗v�f�����s��ƌĂт܂��D�O�̎��ƌ���ׂ�ƁC�S�̍����s�� �͂��̑������킹�ł��邱�Ƃ��킩��܂��D�������킹��ۂɂ͗v�f���̐ߓ_�̔ԍ��t���Ɛߓ_�ԍ��̑Ή��Â����g���܂��D���C�v�f���̐ߓ_�̔ԍ��Â�
�͂��̑������킹�ł��邱�Ƃ��킩��܂��D�������킹��ۂɂ͗v�f���̐ߓ_�̔ԍ��t���Ɛߓ_�ԍ��̑Ή��Â����g���܂��D���C�v�f���̐ߓ_�̔ԍ��Â� ���S�̂̐ߓ_�̔ԍ��Â�
���S�̂̐ߓ_�̔ԍ��Â�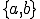 �ɑΉ����Ă���̂ŁC
�ɑΉ����Ă���̂ŁC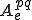 ��
��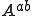 �ɑ������킳��܂��D���̂悤�ȑ������킹�̏������}�[�W(Marge)�ƌĂт܂��D
�ɑ������킳��܂��D���̂悤�ȑ������킹�̏������}�[�W(Marge)�ƌĂт܂��D
��`�������ꂽ�������̉�(���)�́C������(���̖��ł͋��E���������悤��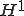 ��Ԃ̕������)�ŁC�G�l���M�[�m�������ŏ��ɂ���悤�ȉ�����邱�Ƃ��킩��܂����D
��Ԃ̕������)�ŁC�G�l���M�[�m�������ŏ��ɂ���悤�ȉ�����邱�Ƃ��킩��܂����D
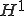 ��Ԃ̒��ł����ɂ��̕�����Ԃł���L���v�f�@��ԏ�̒��ŃG�l���M�[�m�������ŏ��ɂ���悤�ȉ����L���v�f�@�ɂ����Ẳ��ł��D
��Ԃ̒��ł����ɂ��̕�����Ԃł���L���v�f�@��ԏ�̒��ŃG�l���M�[�m�������ŏ��ɂ���悤�ȉ����L���v�f�@�ɂ����Ẳ��ł��D
��Ԋ��ƃe�X�g��������̋�Ԃł���ꍇ�́C�����Galerkin�@�ƌĂт܂��DGalerkin�@�ł̓G�l���M�[�m�����ł����Ƃ�����ɋ߂��悤�ȗL���v�f�@��ԏ�Ō��������ł����邱�Ƃ��킩��܂��D�������Ȃ��痬�̂̂悤�ɃG�l���M�[�����݂��Ȃ��ꍇ�́C��Ԋ��ƃe�X�g����ʂ̋�Ԃ���I�Ԃ��Ƃł�萸�x�̗ǂ����������邱�Ƃ�����܂��D
���Ɏ����̂͗L���v�f�@��͂̑S�̗̂���ł��D
�L���v�f�@�̋[���R�[�h�͈ȉ��̂悤�ɂȂ�܂��D
// �L���v�f�@�̎菇�̋[���R�[�h �@���f������� �A���b�V�������� �B�L���v�f�@��ԏ����� do i=1�C�v�f�� �@�@�C�v�f���Q�Ƃ���ߓ_�f�[�^������Ă��� �@�@�D��`�������ꂽ�x�z��������v�f������ɐϕ����� �@�@�E�ϕ����ē���ꂽ�v�f������̍����s��Ǝc���x�N�g����S�֑̂������킹��D end do �F�S�̍����s��Ǝc���x�N�g�����琬��A���ꎟ�������������āC�X�V�x�N�g���� �G�X�V�x�N�g�����g���ĉ����X�V����D �H�����������
| �L���v�f�@�T�� -���H�w�ɂ������b�Ɖ��p- | �e�r���Y �� |