|TOP Page|

FEMのデータ構造

FEMのデータ構造




Last Update:2007年06月27日


有限要素法では解析領域を単純な形状である要素に分割(メッシュ分割)して、要素の中で積分を計算し、連立一次方程式を作り、それを解くことで解を求める。

基本的に解析領域の単純な形への分割は、ある要素がどの節点を持っているかという配列とある節点の座標を持っている配列によって表現さる。これらをメッシュデータと呼ぶことにする。

しかしながら、連立一次方程式の作成やメッシュの可視化では、メッシュデータは直接使うことは少なく、別のデータに変換することで、初めて使えるようになる。例えば、連立一次方程式の場合、要素によってどの点とどの点が関係づけられるかという、節点から節点へのデータを持つ必要があるが、これはメッシュデータを変換しなければ得られない。

ここでは、要素の型がすべて同じ場合（単一メッシュ）について例を挙げる。

簡単のため２次節点は考慮しないで、節点は要素の角上にのみ存在すると考える。また、幾何学的な面を考えて節点を点と呼ぶことがあるが、ここでは両者は大きな違いはない。

メッシュデータ

FEMではある要素がどの節点を持つかという配列をpoint in elementを省略してinpoelと呼ぶことにする（有限要素法の教科書では大抵lnodsと呼ばれる）例えば要素ielemの中の要素内節点番号ipoelの節点番号ipoinは次のように配列inpoelから取り出すことができる。

ipoin= inpoel [ielem][ipoel]

総要素数をnelem、要素内節点の数をnpoelとすると、この配列inpoelの大きさはnelem×npoelである。

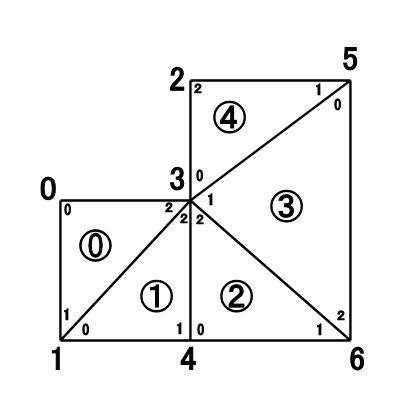
たとえば、上のようなメッシュの場合（但し、○で囲まれた数字は要素番号であり、小さい文字で表している数字は要素内節点番号である。）

inpoel [3][0] = 5、inpoel [3][1] = 3、inpoel [3][2] = 6

のようになる。

****************




節点の座標を格納する配列をcoordsと呼ぶ。節点ipoinのidim座標は次のように書ける

coords [ipoin][idim]

総節点数をnpoin、次元数をndimとすると、この配列coordsの大きさはnpoin×ndimである。

例えば、ndim=2の場合、節点ipoinのｘ座標x、ｙ座標yは次のように書ける

x = coords [ipoin][0]
y = coords [ipoin][1]

派生型のデータ

上で述べたメッシュデータからいかに派生型のデータを作成するかという点について述べる。

点周りの要素

ある要素がどの点をもっているかという情報は配列inpoelが持っている。反対にある点がどの要素に属しているかという情報を持っていれば、後に述べる要素周りの要素や点周りの点を調べる時などに非常に役に立つ。次のようなメッシュの場合は点周りの要素は次のようになる。

点番号 この点を囲む要素番号
0 0
1 0,1
2 4
3 0,1,2,3,4
4 1,2
5 3,4
6 2,3

点周りの要素のデータ構造

１つの点が属する要素の集合をPoint Surrounding Elementを略してelsupという配列に格納する。

一つの要素がいくつの要素に囲まれているかというのは節点によって異なるために、Index配列配列を利用する。Index配列とはある節点の周りの要素が格納されているelsupの場所の先頭を格納している配列で、このIndex配列をelsup_ind とすると、節点ipoinに囲まれている要素の番号ielem0は

ielem0 = elsup [ielsup]  (ielsup=elsup_ind [ipoin] 〜 elsup_ind [ipoin+1]-1)

によって与えられる。

例えば上のようなメッシュの場合は

elsup_ind = {0, 1, 3, 4, 9, 11, 13, 15 }
elsup = { 0, 0, 1, 4, 0, 1, 2, 3, 4, 1, 2, 3, 4, 2, 3 }
nelsup = 15

のようになる。

例えば、節点番号３の周りの要素番号が知りたければelsup_ind [3]=4、elsup_ind [3+1]=9より

配列elsupの４番から9-1=8番を見ればよい。elsupの４番から８番には0,1,2,3,4が入っているはずである。

点周りの要素の作り方

ここでは配列elsup_ind、elsupと値nelsupを具体的に求める方法を説明する。

これらのデータは次のようなステップを用いて生成することができる。


Step1

領域を確保し、初期化した後に、点がいくつの要素に囲まれているかをelsup_ind に格納する

ここで注意するべき点は点ipoinを囲む要素の数をelsup_ind [ipoin+1]に格納していることである。

elsup_ind = new int [npoin+1];
for(int ipoin=0;ipoin<npoin+1;ipoin++){
　 elsup_ind[ipoin] = 0;
}
for(int ielem=0;ielem<nelem;ielem++){
   for(int ipoel=0;ipoel<npoel;ipoel++){
      int ipoin0 = inpoel[ielem][ipoel];
      elsup_ind[ipoin0+1]++;
   }
}


Step2

Step1のelsup_indを前から順番に足しあわせていくことでelsup_ind を作っている。

for(int ipoin=0;ipoin<npoin;ipoin++){
   elsup_ind[ipoin+1] += elsup_ind[ipoin];
}


Step3

nelsupを求め、elsup のメモリを確保

nelsup = elsup_ind[npoin];
elsup = new int [nelsup];


Step4

elsup_ind を変更しながら、elsup を作る。

もともとelsup_indはelsupのIndexを格納する配列である。
つまり、ipoinを囲む要素番号は配列elsupのelsup_ind [ipoin]番目から始まるというように、配列elsup_indは先頭を指し示す配列であった。しかし、ここでは先頭を指し示す配列としてではなく、elsupのどこに値をいれるかという配列として用いる。一度値を入れるとelsup_indの値を１つ増やすことで上書きしないようにしている。この操作によってelsup_indを変更していくと、最終的にelsup_indの値は前に１つずれることになる。

for(int ielem=0;ielem<nelem;ielem++){
   for(int ipoel=0;ipoel<npoel;ipoel++){
      int ipoin0 = inpoel[ielem][ipoel];
      int ielsup0 = elsup_ind[ipoin0];
      elsup[ielsup0] = ielem;
      elsup_ind[ipoin0]++;
   }
}


Step5

elsup_ind を元に戻す。Step4によって配列elsup_indの値は１つ前にずれていることになる。そこでこれを元通りに戻すために配列の値を後ろにずらす。配列の０番目には０が入っていることがわかるので最後にこれをセットする。

for(int ipoin=npoin;ipoin>0;ipoin--){
   elsup_ind[ipoin] = elsup_ind[ipoin-1];
}
elsup_ind[0] = 0;


以上により点を囲む要素のデータを構築することができる。

点周りの点

点周りの点とは要素によってどの点とどの点が接続しているかという情報であり、有限要素法において連立１次方程式を作成する際に行列の非零成分の場所を得る時に使う。これはあくまで要素によって関係づけられている節点のことで、要素の辺による接続とは一般的には異なっている。

例えば上のようなメッシュの場合、点０は要素の辺で接続されている点１、点３に加えて点４も要素によって接続されている。実際０と４の間には辺がないが、仮想的に辺があるとして要素のinternal edgeと言う。上の図では点４は自分以外の全ての節点と接続していることになる。三角形要素や四面体要素はinteranal edgeは持たず、すべての節点同士が辺で接続されている。

点周りの点のデータ構造

点がどの点と要素によって接続しているかという情報をPoint Surrounding Pointを略してpsupという配列に格納する。

一つの点がいくつの点と接続しているかというのは節点によって異なるために、これもまた、データの先頭の場所を表す、Index配列つきの１次元配列で表す。このIndex配列をpsup_indとすると節点ipoinに接続している節点の番号ipoin0は

ipoin0 = psup [ipsup]  (ipsup=psup_ind [ipoin] 〜 psup_ind [ipoin+1]-1)

によって与えられる。

点周りの点の作り方

ここでは配列psup_ind、psupと値npsupを具体的に求める方法を説明する。

これらのデータは次のようなステップを用いて生成することができる。

Step1

点と点との接続の数npsupを求めるステップ

ある節点ipoinが属する要素jelem0について、その要素の中の節点jpoin0が既にカウントされているかどうかを配列lpoinを見ることで調べる。既にカウントされていたらlpoin [jpoin]=ipoinとなっている。そうでなければカウンタicoun0を１つ増やし、この節点が２重にカウントしないためにlpoin [jpoin0]=ipoinを代入する。

lpoin = new int [npoin];
for(int ipoin=0;ipoin<npoin;ipoin++){
   lpoin=-1;
}
int icoun0 = 0;
for(int ipoin=0;ipoin<npoin;ipoin++){
   lpoin[ipoin] = ipoin;
   for(int ielsup=elsup_ind[ipoin];ielsup<elsup_ind[ipoin+1];ielsup++){
      int jelem0 = elsup[ielsup];
      for(int ipoel=0;ipoel<npoel;ipoel++){
         int jpoin0 = inpoel[jelem][ipoel];
         if( lpoin[jpoin0] != ipoin ){
            icoun0++;
            lpoin[jpoin0] = ipoin;
         }
      }
   }
}
npsup = icoun0;

Step2

メモリを確保するステップ

Step1で求めたnpsupを元に配列psupのメモリを確保する

psup_ind = new int [npoin+1];
psup = new int [npsup];

Step3

Step1と同じ手順でpsup_ind、psupを作るステップ

for(int ipoin=0;ipoin<npoin;ipoin++){
   lpoin=-1;
}
icoun0 = 0;
psup_ind[0] = 0;
for(int ipoin=0;ipoin<npoin;ipoin++){
   lpoin[ipoin] = ipoin;
   for(int ielsup=elsup_ind[ipoin];ielsup<elsup_ind[ipoin+1];ielsup++){
      int jelem0 = elsup[ielsup];
      for(int ipoel=0;ipoel<npoel;ipoel++){
         int jpoin0 = inpoel[jelem0][ipoel];
         if( lpoin[jpoin0] != ipoin ){
            psup[icoun0] = jpoin0;
            icoun0++;
            lpoin[jpoin0] = ipoin;
         }
      }
   }
   psup_ind[ipoin+1] = icoun0;
}
delete[] lpoin;

Step4

Step3でもとめたpsupのデータは昇順になっていないので、適当な関数を呼んでソートする。下はＣ＋＋の標準で用意されているソート関数を使った例である。下の関数を使うためには、アルゴリズムヘッダ<algorithm>をインクルードする必要がある。Ｃ言語ならqsort関数を使うのがよい。

for(int ipoin=0;ipoin<npoin;ipoin++){
   int ipsup_begin = psup_ind[ipoin];
   int ipsup_end = psup_ind[ipoin+1];
   std::sort( &psup[ipsup_begin], &psup[ipsup_end] );
}

要素周りの要素

要素周りの要素のデータ構造

要素がどの要素に接しているかという情報はElemnt Surrounding Elementを略してelsuelという配列に格納する。

一つの要素が接している要素の数は一定であり、要素の面（２次元の場合は辺）の数nfaelに等しい。よって次のように２次元配列として値を格納する。要素ielemの面ifaelに接する要素ielem0は

ielem0=elsuel [ielem][ifael]

によって与えられる。外側に面しているために他の要素に接していないような要素がある場合は普通ではとりえない値（例えば-1）を返すようにしておく

要素の面の番号づけ

要素の面（２次元の場合は辺）の番号のつけ方は任意である。Point in Faceを略してlpofaという配列に要素の面がどの節点を持っているかというデータをあらかじめ格納しておく

例えば要素の面ifaelの中の要素面内節点番号ipofaが要素内節点番号ipoelであるという情報は次のように配列lpofaによって与えられる。

ipoel=lpofa [ifael][ipofa]

例えば次のように番号付けをする

三角形要素 四面体要素
face0 lpofa[0][0]=1 lpofa[0][1]=2 lpofa[0][0]=1 lpofa[0][1]=2 lpofa[0][2]=3
face1 lpofa[1][0]=2 lpofa[1][1]=0 lpofa[1][0]=0 lpofa[1][1]=3 lpofa[1][2]=2
face2 lpofa[2][0]=0 lpofa[2][1]=1 lpofa[2][0]=0 lpofa[2][1]=1 lpofa[2][3]=3
face3 lpofa[3][0]=0 lpofa[3][1]=2 lpofa[3][2]=1
****************



下のようなメッシュを考える。但し、要素番号は○で囲まれており、要素内節点番号は小さい数字になっている。それ以外の数字は節点番号である。

この場合配列elsuelは次のようになる。

elsuel [3][0] = 2、 elsuel [3][1] = -1   elsuel [3][2] = 4

要素周りの要素の作り方

ここでは要素ielemの面ifaelに接する要素、つまり、elsuel [ielem][ifael]を具体的に求める方法を説明する。elsuelは全ての要素の中の全ての面についてループさせてこれを調べることで求めることができる。

elsuel [ielem][ifael]は次のようなステップを用いて生成することができる。

Step2からStep4の手順を全ての要素ielem=0〜nelem、ifael=0〜nfaelの間を繰り返すことで全要素の全ての面に対して隣り合う要素を見つけることができる。

以下各ステップについて細かく説明する。

Step1

大きさnpofaの配列inpofaを確保する。また、大きさnpoinの配列lpoinを確保して０でクリアする。

inpofa = new int [npofa];
lpoin = new int [npoin];
for(int ipoin=0;ipoin<npoin;ipoin++){
   lpoin[ipoin] = 0;
}

Step2

要素ielemの面ifael上の節点をinpofaに格納して、その節点についてlpoinを１にする。また、要素の面上のある１点をipoin0とする

for(int ipofa=0;ipofa<npofa;ipofa++){
  int ipoi0 = inpoel[ielem][ lpofa[ifael][ipofa] ];
  inpofa[ipofa] = ipoi0;
  lpoin[ipoin0] = 1;
}

Step3

ipoin0の周りの要素要素jelem0の面jfael0上の点が全て要素ielemの面ifaelに含まれるかlpoinを使って調べる。全て含まれていればelsuel [ielem][ifael]にjelem0を代入して終了、一致していなければ新しい要素の面について調べる。

ipoin0 = inpofa[0];
bool iflg0 = false; 
for(int ielsup=elsup_ind[ipoin0];ielsup<elsup_ind[ipoin0+1];ielsup++){
  int jelem0 = elsup[ielsup];
  if( ielem == jelem0 ) continue;
  for(int jfael=0;jfael<nfael;jfael++){
     iflg0 = true;
     for(int ipofa=0;ipofa<npofa;ipofa++){
        int jpoin0 = inpoel[jelem0][ lpofa[jfael][jpofa] ];
        if( lpoin[jpoin0] == 0 ){
           iflg0 = false;
           break;
        }
     }
     if( iflg0 ){
        elsuel[jelem0][jfael] = ielem;
        break;
     }
  }
  if( iflag0 ) break;
}

Step4

lpoinを元に戻す

for(int ipofa=0;ipofa<npofa;ipofa++){
   lpoin[ inpofa[ipofa] ] = 0;
}

参考文献

Applied CFD Techniques Reynolds Lohner著
Generated by ひとりWiki version 1.13.0